：单片机排序算法大比拼：性能、时间复杂度全解析

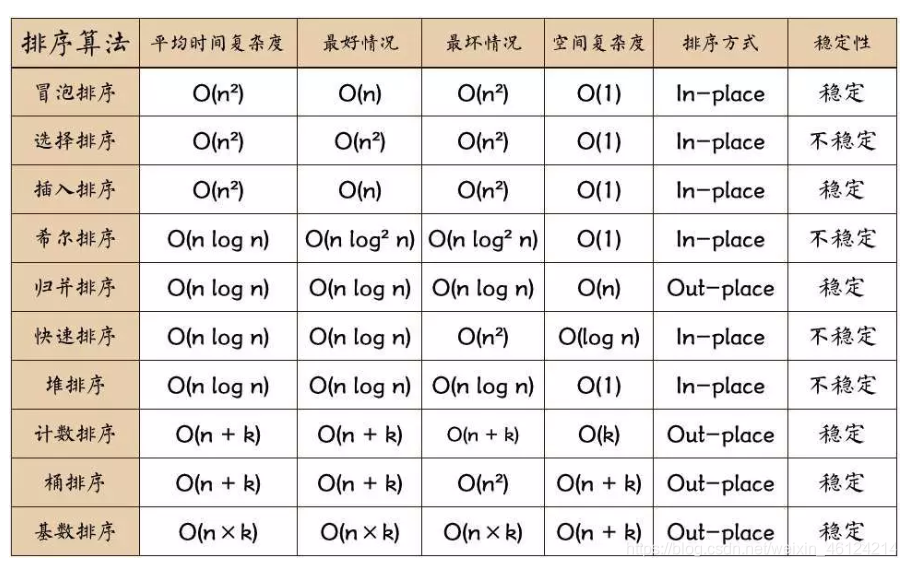
# 1. 单片机排序算法概述

单片机排序算法是用于对单片机中的数据进行排序的一组算法。排序算法通过将数据元素按特定顺序排列，使数据更容易查找、处理和分析。在单片机中，排序算法通常用于处理小规模的数据集，例如传感器读数、控制参数或通信数据。

排序算法根据其工作原理和效率分为不同的类型。最常见的排序算法包括冒泡排序、选择排序和插入排序。这些算法各有优缺点，在不同的应用场景下具有不同的适用性。

# 2. 排序算法理论剖析

### 2.1 冒泡排序

#### 2.1.1 算法原理

冒泡排序是一种简单的排序算法，其基本思想是：将相邻的两个元素进行比较，如果顺序不正确，则交换它们。重复这一过程，直到没有元素需要交换。

#### 2.1.2 时间复杂度分析

冒泡排序的时间复杂度为 O(n^2)，其中 n 为数组中的元素数量。这是因为，对于 n 个元素的数组，需要进行 n-1 次比较和交换。对于每个元素，需要进行 n-1 次比较，因此总共需要 n*(n-1) 次比较。

### 2.2 选择排序

#### 2.2.1 算法原理

选择排序是一种不稳定的排序算法，其基本思想是：在未排序的序列中找到最小（或最大）元素，并将其与序列中的第一个元素交换。然后，在剩余的未排序序列中重复这一过程，直到所有元素都已排序。

#### 2.2.2 时间复杂度分析

选择排序的时间复杂度也是 O(n^2)，与冒泡排序相同。这是因为，对于 n 个元素的数组，需要进行 n-1 次比较和交换。对于每个元素，需要进行 n-1 次比较，因此总共需要 n*(n-1) 次比较。

### 2.3 插入排序

#### 2.3.1 算法原理

插入排序是一种稳定的排序算法，其基本思想是：将未排序的元素插入到已排序的序列中。首先，将第一个元素视为已排序的序列。然后，依次将剩余的元素与已排序序列进行比较，并将其插入到正确的位置。

#### 2.3.2 时间复杂度分析

插入排序的时间复杂度为 O(n^2)，与冒泡排序和选择排序相同。这是因为，对于 n 个元素的数组，需要进行 n-1 次比较和交换。对于每个元素，需要进行 n-1 次比较，因此总共需要 n*(n-1) 次比较。

# 3.1 冒泡排序在单片机中的实现

#### 3.1.1 代码实现

void bubbleSort(int *arr, int len) {
    int i, j;
    for (i = 0; i < len - 1; i++) {
        for (j = 0; j < len - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

#### 3.1.2 性能测试

**参数说明：**

* arr：待排序的数组
* len：数组长度

**代码逻辑分析：**

1. 外层循环（i）遍历数组，控制排序趟数。
2. 内层循环（j）在当前趟中比较相邻元素，将较大的元素后移。
3. 比较元素时，使用临时变量 temp 交换元素值，保证排序稳定性。
4. 经过 len - 1 趟排序后，数组中的元素从小到大排列。

**性能分析：**

* 时间复杂度：O(n^2)，最坏和平均情况下都需要进行 n^2 次比较和交换操作。
* 空间复杂度：O(1)，不需要额外的空间存储。

# 4. 排序算法性能比较

### 4.1 不同算法的性能对比

#### 4.1.1 时间复杂度比较

| 算法 | 时间复杂度 |
|---|---|
| 冒泡排序 | O(n²) |
| 选择排序 | O(n²) |
| 插入排序 | O(n²) |

从时间复杂度上看，三种算法均为 O(n²)，这意味着随着数据规模的增大，算法执行时间将呈平方级增长。

#### 4.1.2 内存消耗比较

| 算法 | 内存消耗 |
|---|---|
| 冒泡排序 | O(1) |
| 选择排序 | O(1) |
| 插入排序 | O(1) |

从内存消耗上看，三种算法均为 O(1)，这意味着算法执行过程中不会分配额外的内存空间。

### 4.2 不同数据规模下的性能影响

#### 4.2.1 数据规模较小时的性能表现

当数据规模较小时（例如，小于 100），三种算法的性能表现相差不大。

#### 4.2.2 数据规模较大时的性能表现

当数据规模较大时（例如，大于 1000），冒泡排序和选择排序的性能明显下降，而插入排序的性能相对较好。

### 4.3 性能比较总结

综合考虑时间复杂度和内存消耗，插入排序在数据规模较大时具有较好的性能表现。对于数据规模较小的情况，三种算法的性能差异不大，可以根据具体需求选择合适的算法。

**代码示例：**

// 冒泡排序
void bubble_sort(int *arr, int len) {
    for (int i = 0; i < len - 1; i++) {
        for (int j = 0; j < len - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

// 选择排序
void selection_sort(int *arr, int len) {
    for (int i = 0; i < len - 1; i++) {
        int min_index = i;
        for (int j = i + 1; j < len; j++) {
            if (arr[j] < arr[min_index]) {
                min_index = j;
            }
        }
        if (min_index != i) {
            int temp = arr[i];
            arr[i] = arr[min_index];
            arr[min_index] = temp;
        }
    }
}

// 插入排序
void insertion_sort(int *arr, int len) {
    for (int i = 1; i < len; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

**逻辑分析：**

* **冒泡排序：**通过不断比较相邻元素并交换位置，将最大的元素逐个移动到数组末尾。
* **选择排序：**在未排序部分中找到最小元素，并将其与当前元素交换位置。
* **插入排序：**将当前元素插入到已排序部分的合适位置。

**参数说明：**

* `arr`：待排序数组
* `len`：数组长度

# 5. 单片机排序算法优化

### 5.1 优化冒泡排序

#### 5.1.1 优化思路

冒泡排序的优化主要集中在减少不必要的比较和交换操作上。以下是一些常见的优化思路：

- **短路优化：**在每次比较时，如果发现相邻元素已经有序，则直接跳过交换操作。
- **哨兵优化：**在数组末尾添加一个哨兵元素，使得在比较过程中，无需再判断是否到达数组末尾。
- **双向冒泡：**同时从数组两端向中间进行冒泡，提高排序效率。

#### 5.1.2 优化代码

void bubbleSortOptimized(int arr[], int size) {
  // 添加哨兵元素
  arr[size] = INT_MAX;

  int swapped;
  do {
    swapped = 0;  // 标记是否发生交换
    // 从数组末尾向中间进行冒泡
    for (int i = size - 1; i >= 1; i--) {
      if (arr[i] < arr[i - 1]) {
        swap(&arr[i], &arr[i - 1]);
        swapped = 1;  // 标记发生交换
      }
    }
    // 从数组开头向中间进行冒泡
    for (int i = 1; i < size; i++) {
      if (arr[i] < arr[i - 1]) {
        swap(&arr[i], &arr[i - 1]);
        swapped = 1;  // 标记发生交换
      }
    }
  } while (swapped);  // 如果没有发生交换，则排序完成

  // 移除哨兵元素
  arr[size] = 0;
}

### 5.2 优化选择排序

#### 5.2.1 优化思路

选择排序的优化主要集中在减少不必要的比较操作上。以下是一些常见的优化思路：

- **最小值索引记录：**在每次比较过程中，记录当前最小值的索引，避免重复比较。
- **有序区优化：**将已经排序的部分作为有序区，后续比较时只比较有序区外的元素。

#### 5.2.2 优化代码

void selectionSortOptimized(int arr[], int size) {
  int minIdx;  // 记录当前最小值的索引

  for (int i = 0; i < size - 1; i++) {
    minIdx = i;  // 初始化最小值索引为当前索引

    // 寻找有序区外的最小值
    for (int j = i + 1; j < size; j++) {
      if (arr[j] < arr[minIdx]) {
        minIdx = j;  // 更新最小值索引
      }
    }

    // 如果最小值索引不为当前索引，则交换元素
    if (minIdx != i) {
      swap(&arr[i], &arr[minIdx]);
    }
  }
}

### 5.3 优化插入排序

#### 5.3.1 优化思路

插入排序的优化主要集中在减少不必要的移动操作上。以下是一些常见的优化思路：

- **二分查找插入：**使用二分查找算法在有序区中找到插入位置，减少移动操作。
- **哨兵优化：**在数组开头添加一个哨兵元素，使得在插入过程中，无需再判断是否到达数组开头。

#### 5.3.2 优化代码

void insertionSortOptimized(int arr[], int size) {
  // 添加哨兵元素
  arr[-1] = INT_MIN;

  for (int i = 1; i < size; i++) {
    int key = arr[i];  // 待插入元素

    // 使用二分查找找到插入位置
    int left = -1;
    int right = i - 1;
    while (left < right) {
      int mid = (left + right) / 2;
      if (arr[mid] < key) {
        left = mid + 1;
      } else {
        right = mid;
      }
    }

    // 移动元素
    for (int j = i; j > left; j--) {
      arr[j] = arr[j - 1];
    }

    // 插入元素
    arr[left + 1] = key;
  }

  // 移除哨兵元素
  arr[-1] = 0;
}

# 6. 单片机排序算法应用实例

### 6.1 数字排序

**6.1.1 需求分析**

在单片机系统中，经常需要对数字数据进行排序，例如：

* 传感器数据排序：对采集到的传感器数据进行排序，以便于后续分析和处理。
* 数据统计排序：对统计数据进行排序，以便于生成报表和图表。

**6.1.2 代码实现**

#include <stdio.h>
#include <stdlib.h>

// 冒泡排序函数
void bubble_sort(int *arr, int len) {
    int i, j;
    for (i = 0; i < len - 1; i++) {
        for (j = 0; j < len - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

int main() {
    int arr[] = {5, 3, 1, 2, 4};
    int len = sizeof(arr) / sizeof(arr[0]);

    bubble_sort(arr, len);

    for (int i = 0; i < len; i++) {
        printf("%d ", arr[i]);
    }

    return 0;
}

### 6.2 字符串排序

**6.2.1 需求分析**

在单片机系统中，也需要对字符串数据进行排序，例如：

* 文件名排序：对文件系统中的文件名进行排序，以便于查找和管理。
* 文本处理排序：对文本数据进行排序，以便于提取关键词和生成摘要。

**6.2.2 代码实现**

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 字符串比较函数
int compare_strings(const void *a, const void *b) {
    return strcmp((char *)a, (char *)b);
}

int main() {
    char *arr[] = {"apple", "banana", "cherry", "dog", "elephant"};
    int len = sizeof(arr) / sizeof(arr[0]);

    qsort(arr, len, sizeof(char *), compare_strings);

    for (int i = 0; i < len; i++) {
        printf("%s ", arr[i]);
    }

    return 0;
}