近似最优算法在组合优化中的深入解析：探索算法与问题的完美契合

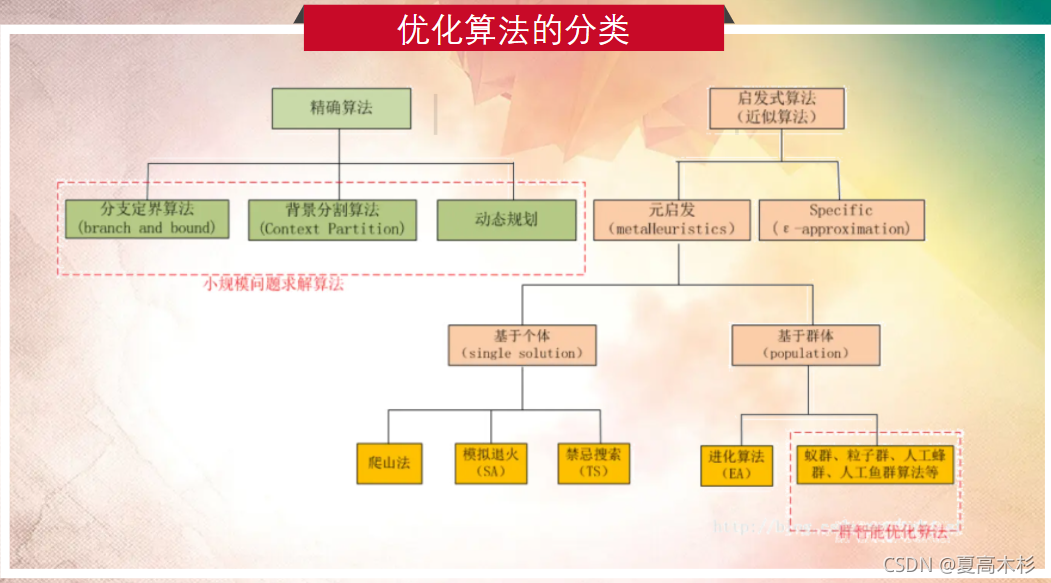
# 1. 近似最优算法概述

近似最优算法是一种在多项式时间内求解NP-hard问题的算法。与精确算法不同，近似最优算法不能保证找到最优解，但可以找到一个近似最优解，其与最优解之间的差距受一个常数因子或多项式因子的限制。

近似最优算法广泛应用于组合优化问题，如旅行商问题、背包问题和最小生成树问题。这些问题通常难以在多项式时间内精确求解，因此近似算法提供了在可接受的时间内获得高质量解的实用方法。

# 2. 近似最优算法的理论基础

### 2.1 近似比和近似算法

近似算法是一种求解组合优化问题的算法，它不能保证找到最优解，但可以找到一个接近最优解的解。近似算法的性能通常用近似比来衡量，近似比定义为近似算法找到的解与最优解的比值。

近似比可以分为以下几类：

* **常数近似比：**近似比为一个常数，例如 2、3/2 等。
* **多项式近似比：**近似比是一个多项式函数，例如 n、n^2 等。
* **对数近似比：**近似比是一个对数函数，例如 log n、log^2 n 等。

### 2.2 贪心算法和局部搜索

贪心算法是一种近似算法，它在每一步都做出局部最优选择，希望最终找到全局最优解。贪心算法的优点是简单易懂，计算复杂度通常较低。但是，贪心算法不能保证找到最优解，而且对于某些问题，贪心算法的近似比可能很差。

局部搜索是一种近似算法，它从一个初始解出发，通过不断对解进行局部改进，最终找到一个局部最优解。局部搜索算法的优点是能够找到较好的近似解，而且对于某些问题，局部搜索算法的近似比可以达到常数。但是，局部搜索算法可能会陷入局部最优解，无法找到全局最优解。

### 2.3 近似方案和多项式时间近似方案

近似方案是一种近似算法，它对于任何输入，都能找到一个近似比为 c 的近似解，其中 c 是一个常数。多项式时间近似方案 (PTAS) 是一种近似方案，它的运行时间是多项式的。

PTAS 对于解决 NP-hard 问题非常有用，因为对于 NP-hard 问题，找到最优解通常是计算上不可行的。PTAS 可以提供一种在多项式时间内找到近似最优解的方法。

**代码块：**

def greedy_tsp(graph):
    """
    使用贪心算法求解旅行商问题。

    参数：
        graph: 图的邻接矩阵。

    返回：
        一个哈密顿回路。
    """

    # 初始化哈密顿回路。
    tour = [0]

    # 剩余的顶点。
    remaining_vertices = set(range(1, len(graph)))

    # 遍历剩余的顶点。
    while remaining_vertices:
        # 选择与当前顶点距离最小的剩余顶点。
        next_vertex = min(remaining_vertices, key=lambda v: graph[tour[-1]][v])

        # 将选择的顶点添加到哈密顿回路中。
        tour.append(next_vertex)

        # 从剩余的顶点中删除选择的顶点。
        remaining_vertices.remove(next_vertex)

    # 返回哈密顿回路。
    return tour

**代码逻辑逐行解读：**

1. 初始化哈密顿回路为只包含第一个顶点的列表。
2. 初始化剩余的顶点为除了第一个顶点之外的所有顶点的集合。
3. 遍历剩余的顶点。
4. 在剩余的顶点中选择与当前顶点距离最小的顶点。
5. 将选择的顶点添加到哈密顿回路中。
6. 从剩余的顶点中删除选择的顶点。
7. 重复步骤 3-6，直到所有顶点都被添加到哈密顿回路中。
8. 返回哈密顿回路。

**参数说明：**

* `graph`：图的邻接矩阵，其中 `graph[i][j]` 表示顶点 `i` 和顶点 `j` 之间的距离。

**近似比分析：**

贪心算法的近似比为 2。这意味着贪心算法找到的哈密顿回路的长度至多是最佳哈密顿回路长度的两倍。

# 3. 近似最优算法在组合优化中的应用

近似最优算法在组合优化中有着广泛的应用，它可以为NP难问题提供可行的解决方案，在保证一定近似比的情况下，有效降低计算复杂度。本章将重点介绍近似最优算法在旅行商问题、背包问题和最小生成树问题中的应用。

### 3.1 旅行商问题

旅行商问题是一个经典的组合优化问题，它要求找到一条最短的回路，访问给定的一组城市并返回出发点。对于大规模的旅行商问题，精确求解往往非常耗时。因此，近似最优算法成为解决此类问题的有效手段。

#### 3.1.1 2-近似算法

2-近似算法是旅行商问题的最简单近似算法之一。它采用贪心策略，每次从当前城市选择距离最近的未访问城市，直到访问所有城市并返回出发点。2-近似算法的近似比为2，这意味着其找到的回路长度不会超过最优回路长度的两倍。

def tsp_2_approx(cities):
    """
    2-近似算法求解旅行商问题

    Args:
        cities: 城市列表

    Returns:
        回路长度
    """
    tour = [cities[0]]
    unvisited = set(cities[1:])

    while unvisited:
        nearest_city = min(unvisited, key=lambda city: distance(tour[-1], city))
        tour.append(nearest_city)
        unvisited.remove(nearest_city)

    return tour_length(tour)

#### 3.1.2 3/2-近似算法

3/2-近似算法是旅行商问题的另一种近似算法，它比2-近似算法具有更好的近似比。3/2-近似算法首先将城市集合划分为两个子集，然后分别求解每个子集的旅行商问题。最后，将两个子集的回路连接起来，形成最终的回路。3/2-近似算法的近似比为3/2，这意味着其找到的回路长度不会超过最优回路长度的3/2倍。

def tsp_32_approx(cities):
    """
    3/2-近似算法求解旅行商问题

    Args:
        cities: 城市列表

    Returns:
        回路长度
    """
    # 将城市集合划分为两个子集
    subsets = partition(cities)

    # 求解每个子集的旅行商问题
    tour1 = tsp_2_approx(subsets[0])
    tour2 = tsp_