近似最优算法在制造业中的质量提升：效率与质量的双重突破

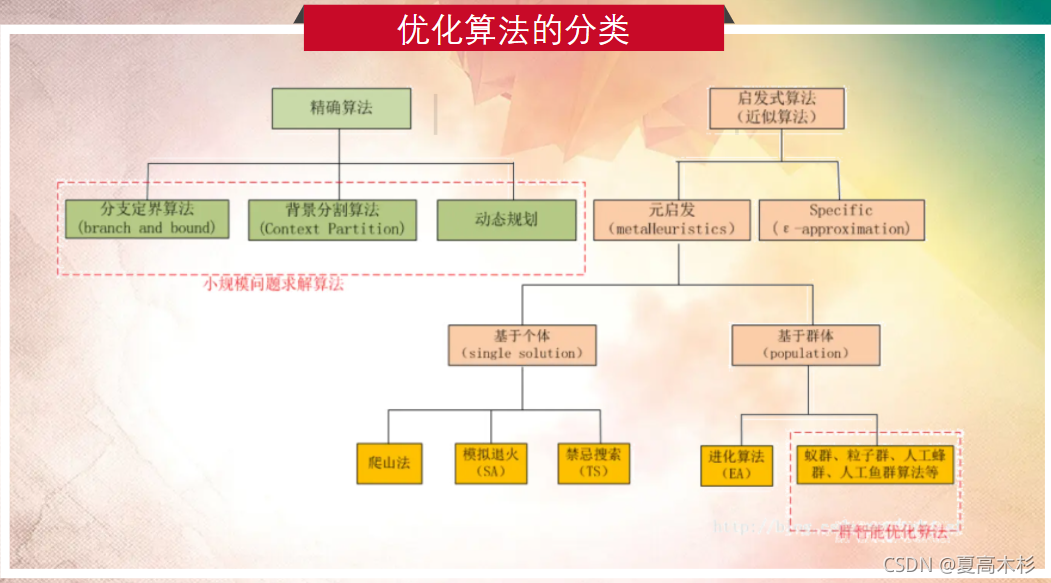
# 1. 近似最优算法简介**

近似最优算法是一种解决复杂优化问题的算法，它通过牺牲精确度来换取计算效率。与精确算法相比，近似最优算法可以在可接受的误差范围内快速找到近似最优解，从而满足实际应用中的需求。

近似最优算法的原理是将复杂的优化问题分解成一系列子问题，并对子问题进行近似求解。通过迭代和优化，近似最优算法逐步逼近最优解。常见的近似最优算法包括贪心算法、启发式算法和随机算法。

# 2. 近似最优算法在制造业中的应用

### 2.1 制造业质量提升的挑战

制造业中，质量提升一直是企业追求的目标。然而，由于制造过程的复杂性和不确定性，实现高质量制造面临着诸多挑战：

- **工艺参数复杂多变：**制造工艺涉及大量参数，如温度、压力、速度等，这些参数的细微变化都会影响产品质量。
- **生产环境动态变化：**制造环境中存在各种干扰因素，如原材料波动、设备故障等，这些因素会影响工艺参数的稳定性。
- **检测成本高昂：**传统质量检测方法往往需要破坏性检测，成本高昂且无法实时监控。

### 2.2 近似最优算法的优势

近似最优算法是一种在有限时间内寻找近似最优解的算法。其在制造业质量提升中具有以下优势：

- **快速求解：**近似最优算法可以在较短时间内找到近似最优解，满足制造业实时优化需求。
- **鲁棒性强：**近似最优算法对参数变化和环境干扰具有较强的鲁棒性，能适应制造过程的动态变化。
- **可解释性好：**近似最优算法的求解过程清晰可解释，便于工程师理解和应用。

### 2.3 近似最优算法在制造业中的具体应用

近似最优算法在制造业中已广泛应用于以下方面：

- **工艺参数优化：**通过近似最优算法优化工艺参数，如温度、压力、速度等，提高产品质量和良品率。
- **生产调度优化：**近似最优算法可以优化生产调度，减少生产时间和成本，提高生产效率。
- **质量检测优化：**近似最优算法可以优化质量检测策略，降低检测成本，提高检测准确性和效率。

#### 2.3.1 工艺参数优化

**代码块：**

import numpy as np
from scipy.optimize import minimize

def objective_function(params):
    # 计算目标函数，即产品质量指标
    quality = ...

# 定义优化参数和约束
params_bounds = [(param_min, param_max), ...]
constraints = [{'type': 'ineq', 'fun': lambda x: ...}]

# 求解近似最优解
result = minimize(objective_function, params_init, bounds=params_bounds, constraints=constraints)

**逻辑分析：**

该代码块使用 `scipy.optimize.minimize` 函数求解工艺参数优化问题。`objective_function` 计算目标函数，即产品质量指标。`params_bounds` 定义优化参数的范围，`constraints` 定义约束条件。求解后，`result` 中包含近似最优解。

#### 2.3.2 生产调度优化

**代码块：**

import pulp

# 定义优化模型
model = pulp.LpProblem("生产调度优化", pulp.LpMinimize)

# 添加决策变量：生产数量
x = pulp.LpVariable.dicts("x", range(num_products), lowBound=0, upBound=max_production)

# 添加目标函数：最小化生产时间
model += pulp.lpSum([production_time[i] * x[i] for i in range(num_products)])

# 添加约束：满足需求
for i in range(num_products):
    model += pulp.lpSum([x[i] for j in range(num_products)]) >= demand[i]

# 求解
model.solve()

**逻辑分析：**

该代码块使用 `pulp` 库构建生产调度优化模型。`x`