近似最优算法在交通运输中的优化策略：物流与交通的效率提升

# 1. 近似最优算法概述

### 1.1 近似最优算法的概念和分类

近似最优算法是一种解决复杂优化问题的算法，它能够在可接受的时间内找到一个接近最优解的解。与精确算法相比，近似最优算法通常具有较高的计算效率，但求得的解的质量可能略低于最优解。

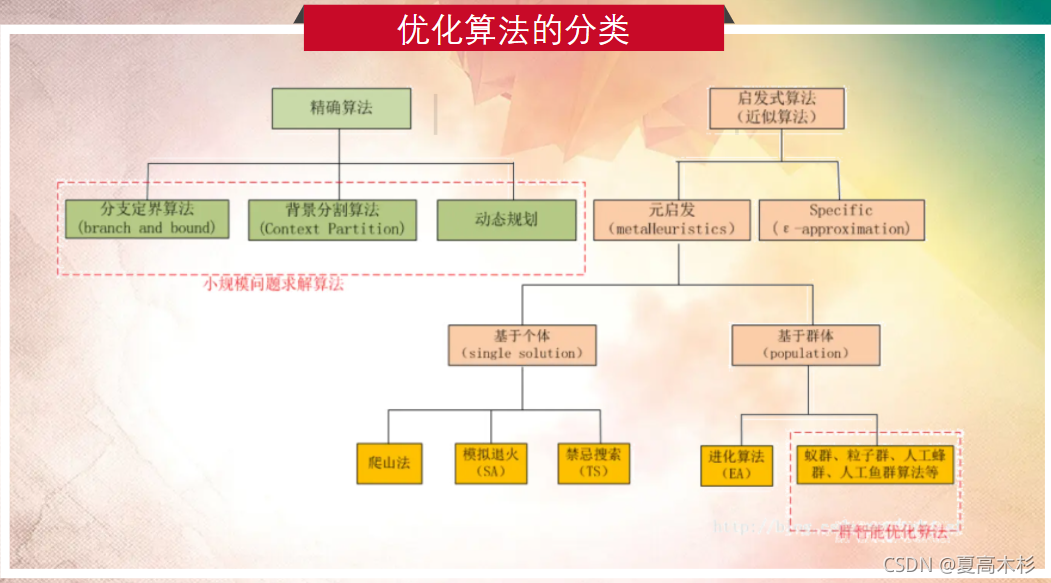
近似最优算法可分为两类：

- **启发式算法：**基于经验和直觉设计的算法，通过迭代搜索和局部优化来寻找解。
- **元启发式算法：**模拟自然现象或生物进化过程的算法，通过随机搜索和群体优化来寻找解。

# 2. 近似最优算法在交通运输中的应用

近似最优算法在交通运输领域有着广泛的应用，能够有效解决复杂且规模庞大的优化问题。本章将重点探讨近似最优算法在车辆路径规划和货物装箱问题中的应用。

### 2.1 车辆路径规划问题

#### 2.1.1 问题描述和建模

车辆路径规划问题（VRP）是一个经典的组合优化问题，其目标是在给定一组客户和车辆的情况下，设计一条或多条车辆路径，以满足所有客户的需求，同时最小化总行驶距离或其他目标函数。VRP的数学模型可以表示为：

min f(x) = ∑_{i=1}^m ∑_{j=1}^n c_{ij}x_{ij}

其中：

* `f(x)` 是目标函数，通常为总行驶距离或总成本
* `x_{ij}` 是决策变量，表示车辆 `i` 是否访问客户 `j`
* `c_{ij}` 是车辆 `i` 从客户 `j` 行驶到客户 `k` 的成本

#### 2.1.2 近似最优算法求解

求解VRP的近似最优算法有很多，其中一种常见的方法是贪心算法。贪心算法在每次迭代中选择当前最优的局部解，逐步构建最终的解决方案。具体步骤如下：

1. 初始化一个空解，并选择一个未访问的客户作为起点。
2. 从起点出发，选择距离最小的未访问客户，将其添加到解中。
3. 重复步骤2，直到所有客户都被访问。
4. 将解中所有车辆的路径连接起来，形成最终的车辆路径。

贪心算法虽然不能保证得到全局最优解，但其计算效率高，在实际应用中可以得到较好的近似解。

### 2.2 货物装箱问题

#### 2.2.1 问题描述和建模

货物装箱问题（BPP）是一个NP难问题，其目标是在给定一组货物和一个容器的情况下，将货物装入容器中，使容器的利用率最大化。BPP的数学模型可以表示为：

max V(x) = ∑_{i=1}^n v_ix_i

其中：

* `V(x)` 是目标函数，表示容器的利用率
* `x_i` 是决策变量，表示货物 `i` 是否装入容器
* `v_i` 是货物 `i` 的体积

#### 2.2.2 近似最优算法求解

求解BPP的近似最优算法有很多，其中一种常见的方法是首次适应算法（FFD）。FFD算法将货物按体积降序排列，然后依次将货物装入容器中。具体步骤如下：

1. 初始化一个空容器。
2. 从体积最大的货物开始，依次尝试将货物装入容器中。
3. 如果货物可以装入容器，则将其装入并更新容器的剩余空间。
4