近似最优算法实现指南：从贪心算法到动态规划，掌握算法精髓

# 1. 算法基础**

算法是计算机科学中解决问题的方法。算法基础是算法设计和分析的基础，包括算法的基本概念、算法的复杂度分析和算法的实现。

算法的基本概念包括算法的定义、算法的特性和算法的分类。算法的复杂度分析包括时间复杂度和空间复杂度，用于衡量算法的效率。算法的实现包括算法的伪代码和算法的代码实现。

# 2. 贪心算法

### 2.1 贪心算法的原理和特点

#### 2.1.1 贪心算法的定义和性质

贪心算法是一种逐步求解问题的算法，它在每一步都做出当前看来最优的选择，而不考虑未来可能的影响。贪心算法具有以下性质：

- **局部最优性：**贪心算法在每一步都做出局部最优的选择，即在当前状态下做出最优选择。
- **无后效性：**贪心算法每一步的选择不影响后续步骤的选择，即后续步骤不受之前选择的影响。

#### 2.1.2 贪心算法的适用场景

贪心算法适用于以下场景：

- **局部最优即全局最优：**当问题的最优解可以通过一系列局部最优选择得到时，贪心算法可以得到全局最优解。
- **子问题独立：**当问题可以分解成一系列相互独立的子问题时，贪心算法可以逐个求解子问题，然后组合得到全局最优解。

### 2.2 贪心算法的应用实例

#### 2.2.1 活动选择问题

**问题描述：**给定一组活动，每个活动都有一个开始时间和结束时间，求出最多可以参加的活动数量。

**贪心算法：**

1. 将活动按结束时间升序排序。
2. 初始化一个空集合 `selected_activities`。
3. 从排序后的活动中依次考虑每个活动。
4. 如果当前活动与 `selected_activities` 中的最后一个活动不冲突（即开始时间大于最后一个活动的结束时间），则将当前活动添加到 `selected_activities` 中。
5. 重复步骤 3-4，直到考虑完所有活动。

**代码示例：**

def activity_selection(activities):
    """
    活动选择问题：给定一组活动，求出最多可以参加的活动数量。

    Args:
        activities (list): 活动列表，每个活动是一个元组 (start, end)

    Returns:
        int: 最多可以参加的活动数量
    """

    # 按结束时间升序排序活动
    activities.sort(key=lambda x: x[1])

    # 初始化选中的活动集合
    selected_activities = []

    # 逐个考虑活动
    for activity in activities:
        # 如果当前活动与选中的最后一个活动不冲突
        if not selected_activities or activity[0] >= selected_activities[-1][1]:
            # 将当前活动添加到选中的活动集合中
            selected_activities.append(activity)

    # 返回选中的活动数量
    return len(selected_activities)

**逻辑分析：**

该贪心算法首先将活动按结束时间排序，然后依次考虑每个活动。如果当前活动与已选中的最后一个活动不冲突，则将其添加到已选中的活动集合中。通过这种方式，贪心算法确保在每一步都选择当前最优的活动，从而得到全局最优解。

#### 2.2.2 最小生成树问题

**问题描述：**给定一个无向连通图，求出一棵生成树，使得生成树的边权和最小。

**贪心算法：**

1. 初始化一个空集合 `edges`，其中包含图中所有的边。
2. 初始化一个空集合 `selected_edges`，其中包含生成树中的边。
3. 从 `edges` 中选择权重最小的边 `e`。
4. 如果 `e` 与 `selected_edges` 中的边不构成环，则将 `e` 添加到 `selected_edges` 中。
5. 重复步骤 3-4，直到 `selected_edges` 中的边数等于图的顶点数减一。

**代码示例：**

from collections import defaultdict
from heapq import heappop, heappush

def prim_algorithm(graph):
    """
    最小生成树问题：给定一个无向连通图，求出一棵生成树，使得生成树的边权和最小。

    Args:
        graph (dict): 图的邻接表表示，其中键是顶点，值为与该顶点相连的边列表

    Returns:
        list: 最小生成树中的边列表
    """

    # 初始化边集合和生成树边集合
    edges = []
    for vertex in graph:
        for neighbor, weight in graph[vertex]:
            edges.append((vertex, neighbor, weight))
    selected_edges = []

    # 初始化最小堆
    pq = [(0, -1, -1)]
    visited = set()

    # 循环直到生成树中边数等于顶点数减一
    while len(selected_edges) < len(graph) - 1:
        # 从最小堆中弹出权重最小的边
        weight, vertex1, vertex2 = heappop(pq)

        # 如果该边不构成环
        if vertex1 not in visited or vertex2 not in visited:
            # 将该边添加到生成树边集合中
            selected_edges.append((vertex1, vertex2, weight))

            # 将该边的两个顶点标记为已访问
            visited.add(vertex1)
            visited.add(vertex2)

            # 将该边的相邻边加入最小堆
            for neighbor, weight in graph[vertex1]:
                if neighbor not in visited:
                    heappush(pq, (weight, vertex1, neighbor))
            for neighbor, weight in graph[vertex2]:
                if neighbor not in visited:
                    heappush(pq, (weight, vertex2, neighbor))

    # 返回最小生成树中的边列表
    return selected_edges

**逻辑分析：**

该贪心算法使用 Prim 算法，从权重最小的边开始，逐步构建生成树。它使用最小堆来维护未选中的边，并确保在每一步都选择权重最小的边。通过这种方式，贪心算法确保在每一步都选择当前最优的边，从而得到全局最优解。

# 3.1 动态规划的原理和特点

**3.1.1 动态规划的定义和思想**

动态规划（Dynamic Programming，简称DP）是一种解决优化问题的算法设计方法，其核心思想是将问题分解成一系列重叠子问题，并通过逐步求解这些子问题来得到最终结果。

动态规划的定义如下：

> 将给定问题分解成一系列重叠子问题，按某种顺序求解这些子问题，并把子问题的解存储起来，以避免重复计算。

动态规划的思想可以用以下步骤概括：

1. **分解问题：**将问题分解成一系列重叠子问题。
2. **确定子问题之间的关系：**找出子问题之间的依赖关系。
3. **确定子问题的最优解：**为每个子问题找到最优解。
4. **合并子问题的解：**将子问题的解合并起来得到最终结果。

**3.1.2 动态规划的适用场景**

动态规划适用于具有以下特征的问题：

* **最优子结构：**问题的最优解包含子问题的最优解。
* **重叠子问题：**子问题在问题的不同部分重复出现。
* **无后效性：**子问题的最优解不影响后续子问题的最优解。

### 3.2 动态规划的应用实例

**3.2.1 0-1背包问题**

**问题描述：**

有一个背包容量为 W，有 n 件物品，每件物品有重量 w_i 和价值 v_i。求如何选择物品装入背包，使得背包中物品的总价值最大。

**动态规划求解：**

1. **状态定义：**dp[i][j] 表示前 i 件物品装入容量为 j 的背包的最大价值。
2. **状态转移方程：**
- 如果 w_i > j：dp[i][j] = dp[i-1][j]
- 如果 w_i <= j：dp[i][j] = max(dp[i-1][j], dp[i-1][j-w_i] + v_i)
3. **边界条件：**
- dp[0][j] = 0 (j >= 0)
- dp[i][0] = 0 (i >= 0)
4. **最优解：**dp[n][W] 表示背包的最大价值。

**代码实现：**

def knapsack(weights, values, capacity):
    n = len(weights)
    dp = [[0] * (capacity + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        for j in range(1, capacity + 1):
            if weights[i - 1] > j:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1])

    return dp[n][capacity]

**逻辑分析：**

代码首先创建了一个二维数组 dp，其中 dp[i][j] 表示前 i 件物品装入容量为 j 的背包的最大价值。然后，代码使用双重循环遍历物品和背包容量，并根据状态转移方程更新 dp 数组。最后，代码返回 dp[n][capacity]，表示背包的最大价值。

**3.2.2 最长公共子序列问题**

**问题描述：**

给定两个字符串 X 和 Y，求 X 和 Y 的最长公共子序列（LCS）。LCS 是 X 和 Y 中的一个子序列，它既是 X 的子序列，也是 Y 的子序列。

**动态规划求解：**

1. **状态定义：**dp[i][j] 表示 X 的前 i 个字符和 Y 的前 j 个字符的最长公共子序列长度。
2. **状态转移方程：**
- 如果 X_i = Y_j：dp[i][j] = dp[i-1][j-1] + 1
- 如果 X_i != Y_j：dp[i][j] = max(dp[i-1][j], dp[i][j-1])
3. **边界条件：**
- dp[0][j] = 0 (j >= 0)
- dp[i][0] = 0 (i >= 0)
4. **最优解：**dp[m][n] 表示 X 和 Y 的最长公共子序列长度。

**代码实现：**

def lcs(X, Y):
    m = len(X)
    n = len(Y)
    dp = [[0] * (n + 1) for _ in range(m + 1)]

    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if X[i - 1] == Y[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

    return dp[m][n]

**逻辑分析：**

代码首先创建了一个二维数组 dp，其中 dp[i][j] 表示 X 的前 i 个字符和 Y 的前 j 个字符的最长公共子序列长度。然后，代码使用双重循环遍历 X 和 Y 的字符，并根据状态转移方程更新 dp 数组。最后，代码返回 dp[m][n]，表示 X 和 Y 的最长公共子序列长度。

# 4. 近似最优算法

### 4.1 近似最优算法的定义和分类

#### 4.1.1 近似最优算法的性质和目标

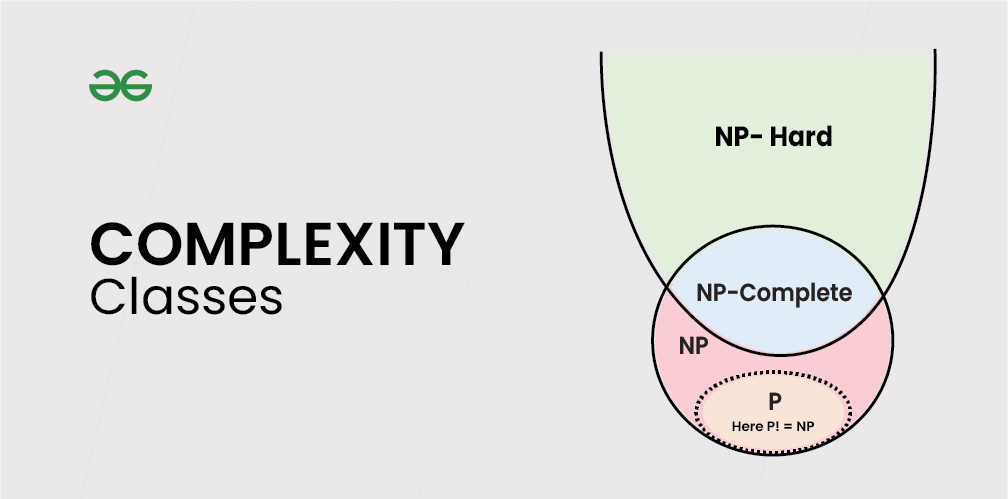
近似最优算法是一种求解优化问题的算法，它不能保证找到最优解，但可以找到一个近似最优解，即一个与最优解相差较小的解。近似最优算法通常用于解决 NP 难问题，即复杂度为 NP 难的优化问题。

近似最优算法的目标是找到一个解，其与最优解的误差在可接受的范围内。误差的度量标准可以是绝对误差、相对误差或近似比。

#### 4.1.2 近似最优算法的分类和特点

近似最优算法可以分为两类：

* **启发式算法：**启发式算法使用启发式规则来指导搜索过程，这些规则通常基于对问题的经验或直觉。启发式算法通常可以快速找到一个近似最优解，但不能保证找到最优解。
* **近似算法：**近似算法使用数学方法来保证找到一个近似最优解，其误差在可接受的范围内。近似算法通常比启发式算法更慢，但可以提供更强的保证。

### 4.2 近似最优算法的应用实例

#### 4.2.1 旅行商问题

旅行商问题是一个 NP 难问题，它要求找到一条最短的路径，该路径访问给定的一组城市并返回起点。

一个近似最优算法是 **2-近似算法**，它保证找到一条路径，其长度至多是最佳路径长度的两倍。2-近似算法使用贪心策略，每次选择当前城市到未访问城市中最短的路径。

def tsp_2_approx(cities):
    """
    求解旅行商问题的 2-近似算法。

    参数：
        cities：城市列表。

    返回：
        一条近似最优路径。
    """

    # 初始化路径。
    path = [cities[0]]

    # 访问所有城市。
    while len(path) < len(cities):
        # 找到当前城市到未访问城市中最短的路径。
        min_distance = float('inf')
        min_city = None
        for city in cities:
            if city not in path and distance(path[-1], city) < min_distance:
                min_distance = distance(path[-1], city)
                min_city = city

        # 将最短路径添加到路径中。
        path.append(min_city)

    # 返回路径。
    return path

#### 4.2.2 图着色问题

图着色问题是一个 NP 难问题，它要求使用最少的颜色为给定图中的顶点着色，使得相邻顶点使用不同的颜色。

一个近似最优算法是 **贪心着色算法**，它使用贪心策略，每次为当前顶点选择一个最少使用的颜色。贪心着色算法可以保证找到一个近似最优解，其颜色数至多是最佳颜色数的 2 倍。

def greedy_coloring(graph):
    """
    求解图着色问题的贪心着色算法。

    参数：
        graph：图。

    返回：
        一个近似最优着色。
    """

    # 初始化着色。
    coloring = {}

    # 访问所有顶点。
    for vertex in graph.vertices:
        # 找到当前顶点最少使用的颜色。
        min_color = None
        min_count = float('inf')
        for color in graph.colors:
            count = 0
            for neighbor in graph.neighbors(vertex):
                if coloring.get(neighbor) == color:
                    count += 1
            if count < min_count:
                min_color = color
                min_count = count

        # 为当前顶点着色。
        coloring[vertex] = min_color

    # 返回着色。
    return coloring

# 5.1 贪心算法的实现

### 5.1.1 贪心算法的伪代码和实现

贪心算法是一种自顶向下的方法，它在每次决策时都选择当前看来最优的方案，而不考虑未来可能的影响。贪心算法的伪代码如下：

def greedy_algorithm(problem):
    """
    贪心算法的伪代码

    :param problem: 问题实例
    :return: 贪心算法的解
    """

    # 初始化解
    solution = []

    # 循环遍历问题实例
    while problem is not empty:
        # 选择当前看来最优的方案
        best_choice = choose_best_choice(problem)

        # 将最优方案添加到解中
        solution.append(best_choice)

        # 从问题实例中移除最优方案
        problem.remove(best_choice)

    # 返回解
    return solution

### 5.1.2 贪心算法的复杂度分析

贪心算法的复杂度取决于问题实例的大小和所使用的具体贪心策略。一般情况下，贪心算法的时间复杂度为 O(n)，其中 n 为问题实例的大小。

**代码逻辑逐行解读：**

1. `def greedy_algorithm(problem):` 定义贪心算法函数，接收问题实例 `problem` 作为输入。
2. `# 初始化解`：使用空列表 `solution` 初始化贪心算法的解。
3. `# 循环遍历问题实例`：使用 `while` 循环遍历问题实例，直到问题实例为空。
4. `# 选择当前看来最优的方案`：调用 `choose_best_choice(problem)` 函数选择当前看来最优的方案。
5. `# 将最优方案添加到解中`：将最优方案添加到 `solution` 列表中。
6. `# 从问题实例中移除最优方案`：从 `problem` 列表中移除最优方案。
7. `# 返回解`：返回贪心算法的解 `solution`。

**参数说明：**

* `problem`: 问题实例，可以是列表、字典或其他数据结构。
* `choose_best_choice(problem)`: 选择当前看来最优方案的函数，具体实现取决于所解决的问题。

**扩展性说明：**

贪心算法的实现可以根据具体问题进行优化，例如使用优先队列或其他数据结构来提高选择最优方案的效率。

# 6.1 算法优化策略

### 6.1.1 算法优化的一般原则

算法优化遵循以下一般原则：

- **时间复杂度优化：**减少算法执行所需的时间。
- **空间复杂度优化：**减少算法执行所需的内存空间。
- **代码可读性优化：**提高代码的可读性和可维护性。
- **通用性优化：**提高算法的通用性，使其适用于更广泛的问题。
- **鲁棒性优化：**提高算法的鲁棒性，使其能够处理各种输入和异常情况。

### 6.1.2 算法优化的手段和技巧

算法优化的手段和技巧包括：

- **代码重构：**重构代码以提高可读性、可维护性和性能。
- **数据结构优化：**选择合适的数据结构来存储和处理数据，以优化时间和空间复杂度。
- **算法替换：**使用更有效的算法来替换效率较低的算法。
- **并行化：**将算法并行化以利用多核处理器或分布式系统。
- **缓存优化：**使用缓存机制来减少对慢速存储器的访问，提高性能。
- **内存管理优化：**优化内存分配和释放，以避免内存泄漏和碎片化。
- **算法参数优化：**调整算法的参数以获得最佳性能。
- **代码分析工具：**使用代码分析工具来识别性能瓶颈和优化机会。