逻辑回归VS线性回归：如何在不同分析场景下做出选择？

# 1. 逻辑回归与线性回归的理论基础

## 1.1 回归分析简介

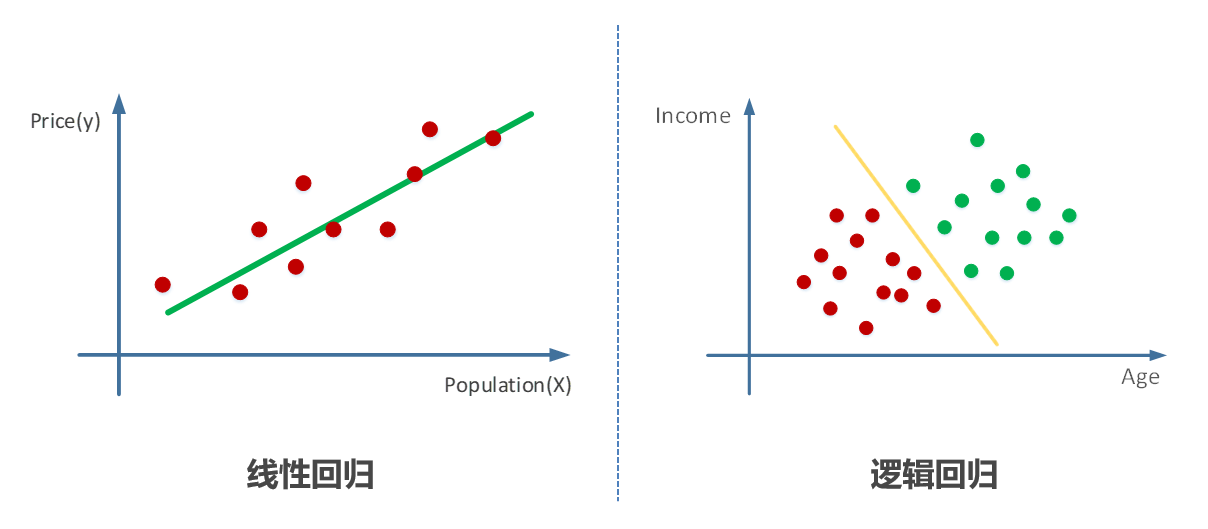
回归分析是一种统计学方法，用于确定两种或两种以上变量间相互依赖的定量关系。在机器学习和数据分析领域，线性回归和逻辑回归是两种基础且广泛使用的回归模型。线性回归处理连续型变量的预测问题，而逻辑回归则常用于分类问题，尤其是在二分类场景。

## 1.2 线性回归的数学表达

线性回归模型试图找到一个线性关系，来描述因变量（目标变量）与一个或多个自变量（解释变量）之间的关系。数学上，单变量线性回归模型可以表示为 `y = a * x + b`，其中`y`是目标变量，`x`是自变量，`a`是斜率，`b`是截距。

## 1.3 逻辑回归的概率解释

逻辑回归与线性回归的主要区别在于它的输出是通过sigmoid函数进行转换的概率值，范围在0和1之间，因此非常适合处理二分类问题。逻辑回归模型的数学表示形式为 `P(Y=1|X) = 1 / (1 + e^-(a * x + b))`，其中`P(Y=1|X)`代表给定`X`时`Y`等于1的概率。

在接下来的章节中，我们将深入探讨线性回归与逻辑回归的具体应用和实践案例。

# 2. 线性回归的实现与应用场景

## 2.1 线性回归模型概述

### 2.1.1 线性回归的基本原理

线性回归（Linear Regression）是统计学中研究变量之间线性关系的模型。在机器学习中，它被广泛应用于预测分析。其基本原理是寻找一个线性方程，用来描述因变量（通常表示为Y）与一个或多个自变量（通常表示为X1, X2, ..., Xn）之间的关系。该方程通常写作：

Y = a + b1*X1 + b2*X2 + ... + bn*Xn + ε

其中，Y是因变量，X1到Xn是自变量，a是截距项，b1到bn是自变量的系数，ε是误差项。

线性回归的核心目标是通过数据来估计这些系数，最小化误差项ε，即模型预测值与实际观测值之间的差距。这可以通过最小二乘法（Ordinary Least Squares, OLS）实现，该方法寻求最佳的系数，使得所有数据点与回归线之间的垂直距离（即残差平方和）最小。

### 2.1.2 线性回归的假设条件

线性回归模型的有效性依赖于以下关键假设：

1. **线性关系**：自变量和因变量之间存在线性关系。
2. **独立性**：观测值之间相互独立，即没有自相关。
3. **同方差性**：不同观测值的误差项具有相同的方差，即残差的方差是恒定的。
4. **正态性**：误差项呈正态分布。
5. **无多重共线性**：自变量之间不存在完全的线性关系，即自变量间没有精确的共线性。

在实践中，需要检查数据是否符合这些假设。例如，可以通过散点图来检查线性关系，用残差图来检查同方差性和正态性，以及利用方差膨胀因子（VIF）来检测多重共线性。

## 2.2 线性回归的实操技巧

### 2.2.1 线性回归模型的建立与评估

建立线性回归模型的第一步是收集和准备数据。数据通常需要进行清洗、编码和标准化。一旦数据准备就绪，就可以使用统计软件或编程语言（如Python或R）来拟合模型。

以下是使用Python的`scikit-learn`库来拟合简单线性回归模型的基本步骤：

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np

# 假设X是特征矩阵，y是目标变量
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([1, 2, 3, 2, 5])

# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建线性回归模型实例
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)

# 预测测试集
predictions = model.predict(X_test)

# 计算模型的均方误差
mse = mean_squared_error(y_test, predictions)
print("模型的均方误差为:", mse)

模型评估通常包括计算R²（决定系数），它表示模型预测的变异占总变异的比例。R²值越接近1，模型拟合效果越好。

### 2.2.2 多元线性回归与变量选择方法

多元线性回归是简单线性回归的扩展，允许我们同时考虑多个自变量对因变量的影响。多元回归分析中，需要特别注意变量选择和模型优化，以避免过拟合和增强模型的解释能力。

变量选择方法包括：

- **向前选择（Forward Selection）**：从没有自变量开始，逐步添加变量。
- **向后消除（Backward Elimination）**：从包含所有变量的模型开始，逐步移除变量。
- **逐步回归（Stepwise Regression）**：结合向前选择和向后消除的方法。

下面是一个使用逐步回归选择变量的例子：

import statsmodels.api as sm

# 添加常数项以考虑截距
X = sm.add_constant(X)

# 假设使用所有的X变量
X_opt = X[:, [0, 1, 2]]  # 我们只是举一个简单的例子来选择变量

# 拟合多元线性回归模型
model = sm.OLS(y, X_opt).fit()

# 输出模型的统计摘要
print(model.summary())

在进行变量选择时，需要检查模型的统计显著性（如p值）、调整R²值以及AIC（赤池信息量准则）或BIC（贝叶斯信息准则）来确定最佳模型。

## 2.3 线性回归的实践应用案例

### 2.3.1 金融领域中的预测分析

在金融领域，线性回归常用于预测股票价格、市场趋势、信用风险等方面。例如，可以使用历史股票数据来预测未来的股票价格。模型可能包含过去几日的股票收盘价、交易量、市场指数等作为自变量。

分析步骤通常包括：

1. 收集股票历史数据。
2. 选择合适的自变量。
3. 使用线性回归模型拟合数据。
4. 进行预测和验证模型准确性。
5. 根据模型结果做出投资决策。

### 2.3.2 市场营销效果的量化分析

市场营销策略的有效性可以通过线性回归来量化。例如，公司可能需要了解广告支出与其带来的销售额之间的关系。通过构建线性回归模型，可以预测在不同的广告支出水平下的预期销售额，进而为营销策略提供数据支持。

具体的分析步骤可能包括：

1. 收集广告投入和销售额的数据。
2. 根据市场活动的类型，选择合适