算法效率提升秘籍：刘次华的随机过程模型优化指南


参考资源链接：[随机过程：刘次华版教材详解与应用](https://wenku.csdn.net/doc/7bhr4euvps?spm=1055.2635.3001.10343)
# 1. 随机过程模型概述

随机过程是概率论中的一类重要的数学模型，它描述了随机现象随时间或其他参数变化的统计规律性。随机过程在IT和相关行业中有着广泛的应用，从网络通信、信号处理到金融市场分析和机器学习等众多领域，随机过程模型都发挥着关键作用。

## 随机过程模型的重要性

在不同的应用领域，随机过程模型的价值体现在其强大的预测能力和建模能力。例如，在金融市场分析中，通过随机过程模型可以预测股票价格的变动趋势，进行风险评估；在通信系统中，随机过程模型用于分析和优化信号传输的稳定性。

## 随机过程模型的分类

随机过程根据其特性可以分为多种类型，包括离散时间随机过程和连续时间随机过程，以及它们的有限状态和无限状态变种。这些不同的模型适用于不同的场景，能够解决各种特定的问题。

在接下来的章节中，我们将深入探讨随机过程模型的理论框架、优化理论基础，并探讨如何在实际应用中发挥作用，以及如何通过优化技术提升模型性能。

# 2.1 随机过程模型的理论框架

随机过程是研究随机变量序列随时间或其他参数变化的数学模型，它是现代概率论和随机分析的核心部分。理解随机过程的基础理论对于深入应用该模型至各种复杂的现实问题至关重要。

### 2.1.1 随机过程的定义和分类

随机过程是一组随机变量的集合，这些变量通过它们的参数（通常是时间）相关联。给定一个集合 \(T\)，如果对每一个 \(t \in T\)，\(X_t\) 是一个随机变量，那么 \(\{X_t : t \in T\}\) 就构成了一个随机过程。

例如，布朗运动（Brownian motion），又名维纳过程，是一种连续时间随机过程，其定义为：

- \(W_0 = 0\)，过程在时间为0时处于原点。
- 对于任意 \(s < t\)，增量 \(W_t - W_s\) 是一个均值为0，方差为 \(t-s\) 的正态分布随机变量。
- 对于任意 \(n\) 个时间点 \(0 < t_1 < t_2 < ... < t_n\)，增量 \(W_{t_1}, W_{t_2}-W_{t_1}, ..., W_{t_n}-W_{t_{n-1}}\) 是独立的。

随机过程按照不同的分类标准，可有多种类型。按照时间参数的类型，可分为离散时间随机过程和连续时间随机过程。而根据状态空间的性质，可以区分为有限状态随机过程、可数状态随机过程和连续状态随机过程。

### 2.1.2 随机过程的统计特性和参数估计

随机过程的统计特性是通过其统计量如均值函数、方差函数、协方差函数等来表征的。均值函数 \(\mu(t)\) 表示过程在时刻 \(t\) 的平均行为；方差函数 \(\sigma^2(t)\) 描述了随机过程在该时刻的变化度量；而协方差函数则揭示了不同时间点随机变量的统计相关性。

参数估计则是从观测到的数据中估计出随机过程的未知参数。常见的参数估计方法包括极大似然估计（MLE）和贝叶斯估计。这两种方法都有其理论基础和具体应用的场景，选择合适的方法对于准确建模随机过程至关重要。

例如，对于泊松过程，一个常见的连续时间随机过程，我们可以通过观察事件发生的次数与时间间隔来估计其强度参数 \(\lambda\)。通过最大化似然函数，我们可以得到参数估计的公式。

## 2.2 算法复杂度分析

在研究和应用随机过程时，算法复杂度分析是一个必不可少的环节。它帮助我们评估算法在处理数据时的性能表现，并指导我们在实际应用中选择最合适的算法。

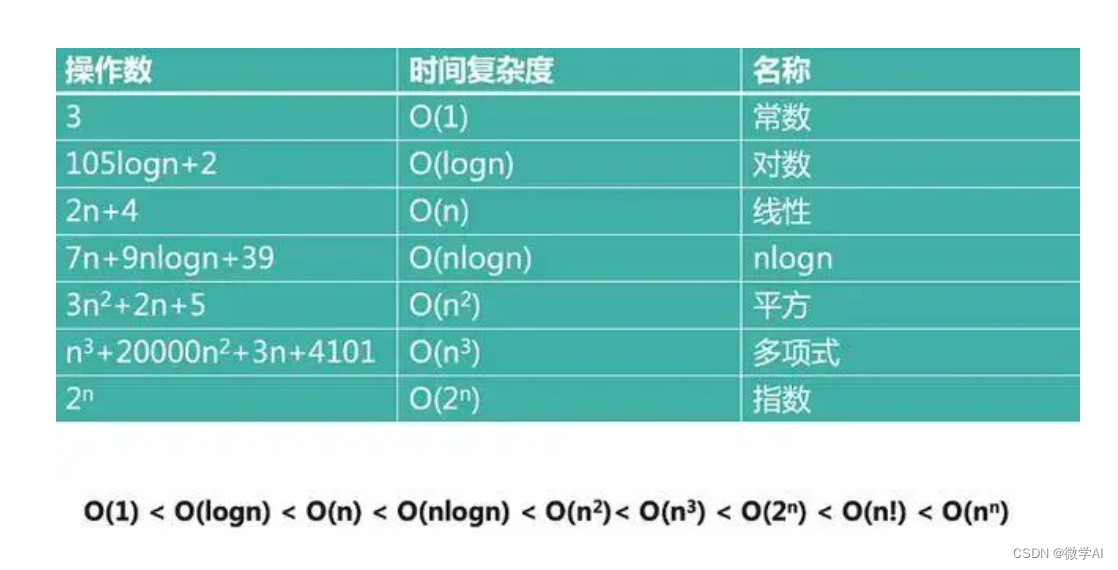
### 2.2.1 时间复杂度和空间复杂度

时间复杂度是指完成一个算法所需要的计算时间，通常与输入数据的规模 \(n\) 有关，用大O符号 \(O(f(n))\) 来表示。空间复杂度则描述了算法执行过程中所需的存储空间，同样地，它也是输入数据规模的一个函数。

例如，对一个简单的随机过程进行模拟，可能会涉及到大量的随机数生成。如果每个随机数生成都需要 \(O(1)\) 的时间复杂度，那么对于 \(n\) 个随机数的生成，整个过程的时间复杂度是 \(O(n)\)。

### 2.2.2 算法的上下界分析

算法的上下界是指算法性能的最坏和最好情况。分析算法的上下界有助于预测算法在不同情况下的表现，从而为算法的选择提供理论依据。

举个例子，一个排序算法的最坏情况时间复杂度可能高达 \(O(n^2)\)，而它的最佳情况则可能是 \(O(n \log n)\)。在实际应用中，我们应该根据数据的分布和算法的使用场景来选择合适的算法。

## 2.3 优化算法的设计原则

优化算法是处理和分析随机过程模型时必不可少的工具。设计一个高效的优化算法，需要综合考虑多个方面，包括稳健性、鲁棒性、可伸缩性和适应性。

### 2.3.1 稳健性和鲁棒性的考量

稳健性是指算法面对不同输入数据时的性能稳定性。鲁棒性强调的是算法对异常值和噪声的抵抗能力。

例如，在进行随机过程的参数估计时，如果估计值对于输入数据的小的变动十分敏感，那么可以说该估计方法稳健性和鲁棒性不足。为此，可以采用抗差估计（robust estimation）等方法，以提高算法的稳健性和鲁棒性。

### 2.3.2 算法的可伸缩性和适应性

可伸缩性关注的是算法性能是否随着问题规模的增加而线性或接近线性变化。而适应性则强调算法是否能适应不同种类的输入数据。

例如，对于大规模数据集的随机过程模拟，传统的算法可能在时间复杂度和空间复杂度上难以扩展。然而，使用分而治之的策略，或并行计算技术，可以极大地提高算法的可伸缩性。适应性方面，可以通过学习数据的结构特征来自动调整算法参数，以适应不同的数据分布。

优化算法的设计是一个复杂但又极富挑战性的领域。理解其设计原则，能够帮助我们更好地应对实际问题，提升随机过程模型的实际应用效果。

# 3. ```
# 第三章：随机过程模型的实际应用

随机过程模型在IT行业和相关领域有着广泛的实际应用。本章将深入探讨随机过程模型在数据分析、信号处理以及金融分析中的具体应用场景，旨在揭示模型的实际效用和优化策略。

## 3.1 随机过程模型在数据分析中的应用

数据分析是随机过程模型应用的一个重要领域，通过使用这些模型，我们能够对不确定性进行建模，从而进行更为准确的预测。

### 3.1.1 预测和建模的实际案例分析

在数据科学领域，使用随机过程模型进行预测和建模已成为常规操作。以下是对一个实际案例的分析：

假设有一家电商公司，想要通过历史销售数据预测未来的销售趋势。为了准确预测，我们可以利用随机过程模型，如自回归积分滑动平均模型（ARIMA），来捕捉数据中的趋势和季节性变化。以下是使用ARIMA模型的一个简单案例代码：

from statsmodels.tsa.arima.model import ARIMA

# 假设 sales_data 是一个包含历史销售数据的数组
model = ARIMA(sales_data, order=(5,1,0))  
results = model.fit()  

# 使用模型进行未来销售趋势的预测
forecast = results.forecast(steps=5)  
print(forecast)

在这个示例中，我们首先从 `statsmodels` 库中导入了 `ARIMA` 模型，然后使用历史销售数据创建了模型实例，并指定了模型的阶数。最后，我们对模型进行了拟合，并进行了未来五步的销售趋势预测。

### 3.1.2 数据集的准备和预处理方法

在进行模型分析之前，数据集的准备和预处理是不可或缺的步骤。数据预处理可能包括数据清洗、异常值处理、特征提取、规范化以及数据划分等。这里我们主要关注随机过程模型数据集的特殊处理方法。

以时间序列数据为例，可能需要进行以下处理步骤：

import numpy as np
import pandas as pd

# 假设 raw_data 是从某个数据库中获取的原始时间序列数据
raw_data = pd.read_csv('sales_data.csv')

# 将数据转换为时间序列格式，并进行标准化
ts_data = pd.Series(raw_data['sales'].values)
ts_data.index = pd.date_range(start='2020-01-01', periods=len(raw_data), freq='M')
ts_data = (ts_data - ts_data.mean()) / ts_data.std()

# 接下来进行数据的分割为训练集和测试集
train_size = int(len(ts_data) * 0.8)
train_data = ts_data[:train_size]
test_data = ts_data[train_size:]

在上述代码中，我们首先读取了原始数据，将其转换为时间序列格式，并进行了标准化处理。然后，我们按照80/20的比例将数据集分割为训练集和测试集。

## 3.2 随机过程模型在信号处理中的应用

信号处理是随机过程模型应用的另一个核心领域，特别是在噪声过滤和特征提取方面。

### 3.2.1 信号的噪声过滤和特征提取

在信号处理中，随机过程模型可以用来构建高效的噪声过滤器，从而提取出信号中的重要特征。一个常见的方法是使用卡尔曼滤波器。

以下是一个使用卡尔曼滤波器对时间序列信号进行噪声过滤的Python代码示例：

import numpy as np

# 定义卡尔曼滤波器的参数
F = np.array([[1., 1.],
              [0., 1.]])
H = np.array([[1., 0.]])
Q = np.eye(2) * 0.01
R = 1.
x = np.zeros((2, 1)) # 初始状态
P = np.eye(2) # 初始估计误差

# 假设 measurements 是观测到的带有噪声的信