随机性分析：刘次华的随机过程深入探讨


参考资源链接：[随机过程：刘次华版教材详解与应用](https://wenku.csdn.net/doc/7bhr4euvps?spm=1055.2635.3001.10343)
# 1. 随机过程基础理论

随机过程是数学的一个分支，涉及系统行为随时间演化的概率模型。在这一章中，我们将引入随机过程的基本概念，为理解更复杂的理论奠定基础。

## 1.1 随机变量与随机过程的定义

随机变量是随机过程中最基本的概念，它是从概率空间到实数或更高维空间的一个可测函数。随机过程则是随机变量序列，其中每个变量对应一个时间点。

\text{定义} \quad X: \Omega \times T \rightarrow \mathbb{R}

这里，$\Omega$ 表示样本空间，$T$ 是时间集，$X$ 是随机过程。

## 1.2 随机过程的分类

根据时间集的不同，随机过程可以分为离散时间随机过程和连续时间随机过程。离散时间过程的实例包括时间序列，而连续时间过程常见于模拟物理现象。

- **离散时间随机过程**：在特定时刻取值，如股票价格的日变化。
- **连续时间随机过程**：可以在任意时间取值，如股票价格的连续变化。

## 1.3 随机过程的基本性质

了解随机过程的基本性质是分析其行为和应用的第一步。这些性质包括马尔可夫性、平稳性和独立增量等。

- **马尔可夫性**：一个随机过程是马尔可夫的，如果给定当前状态，未来状态独立于过去状态。
- **平稳性**：统计特性不随时间变化的随机过程具有平稳性。
- **独立增量**：过程的增量相互独立。

这些性质对于建立和解释随机过程模型至关重要，构成了后续深入学习的基石。

在下一章节中，我们将详细探讨随机过程的数学模型，进一步理解其结构和功能。

# 2. 随机过程的数学模型

随机过程的数学模型是理解随机现象的基石。在这一章节中，我们将深入探讨随机过程的基本概念、特性以及它们在不同情境下的应用。通过对离散与连续时间随机过程、概率描述和极限定理的分析，我们将建立起对随机过程深刻的理解。

## 2.1 离散与连续时间随机过程

随机过程可以按照时间参数的性质划分为离散时间随机过程和连续时间随机过程。它们各自具有独特的特点和应用场景，下面分别进行探讨。

### 2.1.1 离散时间马尔可夫链

离散时间马尔可夫链（Markov Chain）是描述一个系统状态随时间变化的随机过程，其中未来的状态仅依赖于当前状态，与过去的状态无关，这种性质称为马尔可夫性质。

马尔可夫链由状态空间和转移概率矩阵来定义。状态空间表示系统可能处于的所有状态集合，而转移概率矩阵则描述了从一个状态转移到另一个状态的概率。

(* 马尔可夫链状态转移示例矩阵 *)
 переходы = {{0.7, 0.2, 0.1}, {0.3, 0.5, 0.2}, {0.2, 0.3, 0.5}};

在实际应用中，我们经常需要计算长期状态分布，也就是系统在经过足够长的时间后，各状态的概率分布。这通常涉及到求解线性方程组或者应用幂方法来计算状态转移矩阵的特征值和特征向量。

### 2.1.2 连续时间马尔可夫过程

连续时间马尔可夫过程（Continuous-time Markov Chain, CTMC）扩展了离散时间马尔可夫链的概念，允许在任意两个状态之间的时间间隔是随机的。

在连续时间马尔可夫过程中，状态之间的转移发生在连续时间参数上，且转移时间通常假设服从指数分布。指数分布的无记忆性质与马尔可夫性质相结合，使得连续时间马尔可夫过程在模型构建上非常有用。

import numpy as np

# 指定状态转移率矩阵
Q_matrix = np.array([[ -2, 1, 1],
                     [  1, -2, 1],
                     [  1, 1,  -2]])

# 使用scipy计算稳态分布
from scipy.linalg import eig

eigenvalues, eigenvectors = eig(np.transpose(-Q_matrix))
steady_state = eigenvectors[:, np.argmax(eigenvalues)]
steady_state /= steady_state.sum()

在上述Python代码中，我们使用了`scipy.linalg.eig`函数来计算矩阵`Q`的特征值和特征向量，进而求解连续时间马尔可夫链的稳态分布。

## 2.2 随机过程的概率描述

随机过程的概率描述涉及概率测度和期望值的定义，这是理解和分析随机过程的定量基础。

### 2.2.1 概率测度与期望

概率测度描述了随机过程在不同样本路径上的分布情况。对于一个随机过程{X(t), t ∈ T}，每个时间点t处的X(t)都是一个随机变量，并且整个过程可以看作是在时间集合T上的随机变量族。

随机过程的期望值是一个时间函数，表示在每个时间点t上随机变量X(t)的平均行为。例如，在马尔可夫链中，状态的期望值可以通过状态转移概率矩阵和初始状态概率分布来计算。

### 2.2.2 独立增量过程与平稳增量过程

独立增量过程指的是在任意不相交的时间区间内，随机过程的增量是相互独立的。这意味着过程的未来行为不受过去历史的影响，只与当前状态有关。

平稳增量过程则要求增量的分布只依赖于时间区间的长度，而不依赖于具体的时间点。这种特性使得平稳增量过程在许多领域都有广泛的应用，如排队理论和保险模型。

## 2.3 随机过程的极限定理

随机过程的极限定理是研究随机过程渐近行为的基本工具，它涉及弱大数定律、强大数定律和中心极限定理等概念。

### 2.3.1 弱大数定律与强大数定律

弱大数定律（Law of Large Numbers）描述了随机变量序列平均值的稳定性质。对于独立同分布的随机变量序列，其平均值几乎必然收敛到期望值。

强大数定律（Strong Law of Large Numbers）则是弱大数定律的加强版本，它表明随机变量序列的平均值在概率上几乎必然收敛到期望值。

### 2.3.2 中心极限定理在随机过程中的应用

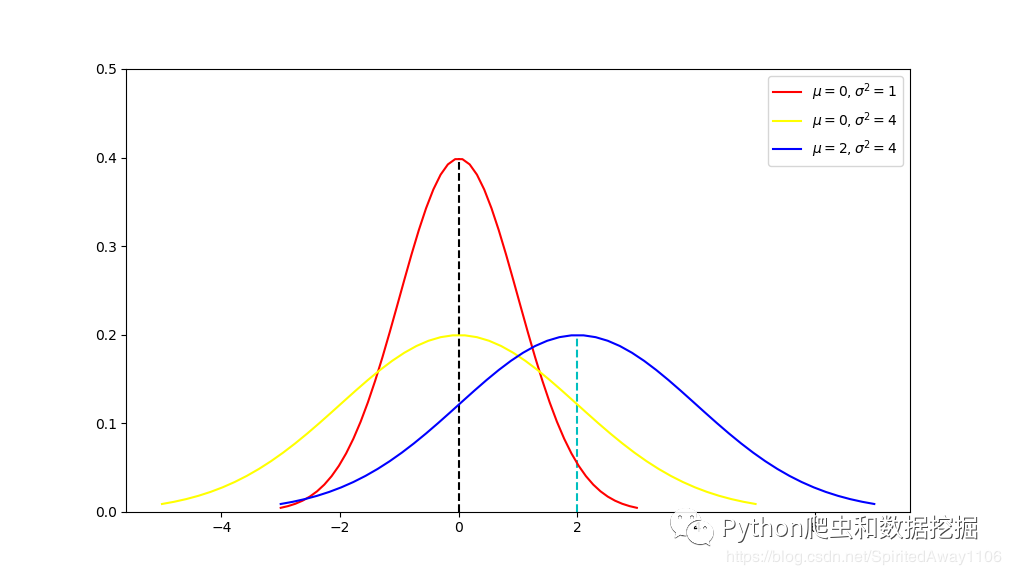
中心极限定理（Central Limit Theorem）说明了随机变量序列的和经过适当的标准化后，其分布趋近于正态分布。在随机过程中，中心极限定理为理解复杂过程的极限行为提供了有力工具。

对于一些特定类型的随机过程，如独立增量过程，中心极限定理可以用来推断过程的极限分布。这对于金融、保险和工程领域等实际问题的建模和分析非常有用。

以上内容提供了一个关于随机过程数学模型的全面概览。从离散和连续时间随机过程，到概率测度与期望值，再到极限定理，本章深入浅出地探讨了随机过程的数学理论和应用。通过这一章节的阅读，读者应能够对随机过程的理论基础有一个清晰的认识，并为更深入的学习和研究打下坚实的基础。

# 3. 随机过程的分析技术

## 3.1 随机过程的时间序列分析

随机过程的时间序列分析是研究按时间顺序排列的数据点集合，这些数据点通常由随机过程生成。通过对时间序列的深入分析，我们可以识别其结构并预测未来值。下面将介绍三种基本的时间序列模型：自回归模型（AR）、移动平均模型（MA）和自回归移动平均模型（ARMA）以及其扩展的自回归积分滑动平均模型（ARIMA）。

### 3.1.1 自回归模型（AR）

自回归模型是时间序列分析中最基本的线性模型之一。其假设当前时间点的数据是其先前时间点数据的线性组合加上一个误差项。对于一个AR(p)模型，即p阶自回归模型，可以表达为：

\[ Y_t = c + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \cdots + \phi_p Y_{t-p} + \epsilon_t \]

这里，\(Y_t\) 是当前时间点的观测值，\( \phi_1, \phi_2, \ldots, \phi_p \) 是模型的参数，\(c\) 是常数项，而 \( \epsilon_t \) 是误差项，通常假设其服从白噪声分布。

#### 代码实现：

import numpy as np
import statsmodels.api as sm

# 假设我们有下面的一组时间序列数据
data = np.array([1.2, 1.3, 1.25, 1.24, 1.25, 1.27])

# 使用statsmodels来拟合AR模型
p = 2 # AR模型的阶数
model = sm.tsa.AR(data).fit(maxlag=p)
print(model.params)

执行这段代码后，我们会得到AR模型的参数估计。实际中，模型的阶数通常通过AIC或BIC标准来确定，以选择最佳的模型。

### 3.1.2 移动平均模型（MA）

移动平均模型是另一种线性模型，它表达了时间序列中的一个值是如何通过先前的预测误差的线性组合加上常数项来计算的。对于一个MA(q)模型，可以写成：

\[ Y_t = \mu + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q} \]

这里，\( \mu \) 是时间序列的均值，\( \theta_1, \theta_2, \ldots, \theta_q \) 是模型参数，而 \( \epsilon_t \) 依旧是误差项。

### 3.1.3 ARMA与ARIMA模型

ARMA模型是AR和MA模型的组合，可以描述很多平稳时间序列的特征。模型表达式如下：

\[ Y_t = c + \phi_1 Y_{t-1} + \cdots + \phi_p Y_{t-p} + \epsilon_t + \theta_1 \epsilon_{t-1} + \cdots + \theta_q \epsilon_{t-q} \]

而ARIMA模型是ARMA模型的扩展，它可以用于非平稳时间序列。ARIMA模型首先通过差分将非平稳时间序列转化为平稳时间序列，然后应用ARMA模型的框架。

#### 模型选择：

选择合适的时间序列模型通常需要进行一系列诊断检查。这些检查包括平稳性测试（例如ADF测试），ACF和PACF图，以及残差的白噪声检验等。

## 3.2 随机过程的谱分析

### 3.2.1 谱密度函数的概念

谱密度函数是描述时间序列中频率成分如何分布的数学函数。对于一个随机过程 \( X_t \)，其谱密度函数 \( S(\omega) \) 定义为：

\[ S(\omega) = \sum_{\tau=-\infty}^{\infty} \gamma(\tau) e^{-i\omega\tau} \]

其中 \( \gamma(\tau) \) 是时间序列的自协方差函数，而 \( \omega \) 是角频率。

### 3.2.2 谱分析在信号处理中的应用

在信号处理中，谱分析用于分析和处理含有大量数据的信号。例如，在语音识别和音乐分析中，谱分析能够帮助识别不同声音信号的频率特征，有助于进一步的数据处理和特征提取。

#### 案例研究：

考虑一个音乐识别的案例，一个音频文件可以视为一个时间序列。通过计算音频文件的谱密度，我们可以识别其中的频率成分，进而分析音符和和弦。

## 3.3 随机过程的滤波与预测

### 3.3.1 卡尔曼滤波的基本原理

卡尔曼滤波是一种高效的递归滤波器，用于估计线性动态系统的状态。在随机过程中，卡尔曼滤波通过融合观测数据和过程模型，不断更新状态估计，从而最小化估计误差的协方差。

#### 卡尔曼滤波过程：

1. **初始化**：设定初始状态估计和误差协方差矩阵。
2. **预测**：基于模型预测下一个状态和误差协方差。
3. **更新**：通过观测数据更新状态估计和误差协方差。

### 3.3