MATLAB线性拟合在数据分析中的作用：从数据中提取洞察

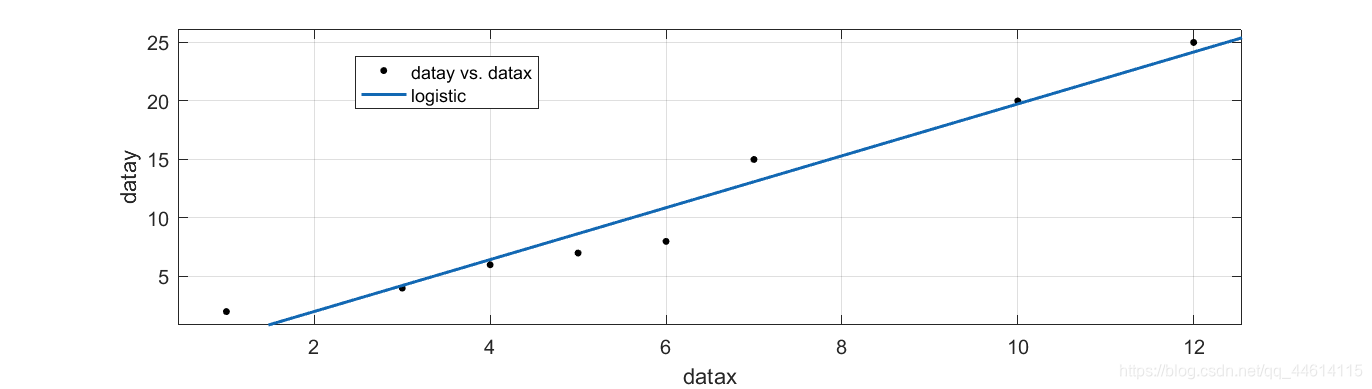
# 1. MATLAB线性拟合概述

MATLAB线性拟合是一种强大的数据分析技术，用于建立和评估线性模型，描述两个或多个变量之间的关系。线性模型假设变量之间存在线性关系，即一条直线可以很好地拟合数据点。

MATLAB提供了一系列函数和工具，用于执行线性拟合，包括创建模型、估计参数和评估拟合优度。线性拟合在各种应用中非常有用，包括数据趋势分析、相关性分析和预测。

# 2. 线性拟合理论基础

### 2.1 线性回归模型

线性回归模型是统计学中用于描述两个或多个变量之间线性关系的数学模型。它假设因变量（响应变量）与自变量（解释变量）之间存在线性关系。

#### 2.1.1 最小二乘法原理

最小二乘法原理是线性回归模型中最常用的参数估计方法。其目标是找到一组参数，使模型预测值与实际值之间的平方误差和最小。

最小二乘法原理的数学表达式为：

min ∑(y_i - f(x_i, β))^2

其中：

* y_i 是因变量的实际值
* x_i 是自变量的观测值
* f(x_i, β) 是模型预测值
* β 是模型参数

#### 2.1.2 线性回归方程的求解

对于一个简单的线性回归模型（一个因变量和一个自变量），线性回归方程可以表示为：

y = β_0 + β_1x

其中：

* β_0 是截距项，表示当自变量为 0 时的因变量值
* β_1 是斜率，表示因变量随着自变量变化而变化的速率

线性回归方程可以通过最小二乘法原理求解，具体步骤如下：

1. 计算自变量和因变量的均值：

   x̄ = 1/n ∑x_i
   ȳ = 1/n ∑y_i

2. 计算自变量和因变量的协方差：

   cov(x, y) = 1/n ∑(x_i - x̄)(y_i - ȳ)

3. 计算斜率：

   β_1 = cov(x, y) / var(x)

4. 计算截距：

   β_0 = ȳ - β_1x̄

### 2.2 模型评估与选择

在拟合线性回归模型后，需要对模型进行评估和选择，以确保模型的准确性和适用性。

#### 2.2.1 拟合优度指标

拟合优度指标用于衡量模型预测值与实际值之间的接近程度。常用的拟合优度指标包括：

* **均方误差（MSE）：**模型预测值与实际值之间的平方误差的平均值。
* **均方根误差（RMSE）：**MSE 的平方根，表示模型预测误差的平均幅度。
* **决定系数（R^2）：**模型解释因变量变异程度的比例。

#### 2.2.2 模型选择准则

模型选择准则用于在多个候选模型中选择最优模型。常用的模型选择准则包括：

* **赤池信息准则（AIC）：**一种基于信息论的准则，考虑模型的拟合优度和模型复杂度。
* **贝叶斯信息准则（BIC）：**一种基于贝叶斯统计的准则，与 AIC 类似，但对模型复杂度的惩罚更大。
* **交叉验证：**将数据集划分为训练集和测试集，在训练集上训练模型，在测试集上评估模型，以避免过拟合。

# 3. MATLAB线性拟合实践

### 3.1