MATLAB线性拟合全方位指南：涵盖所有关键方面

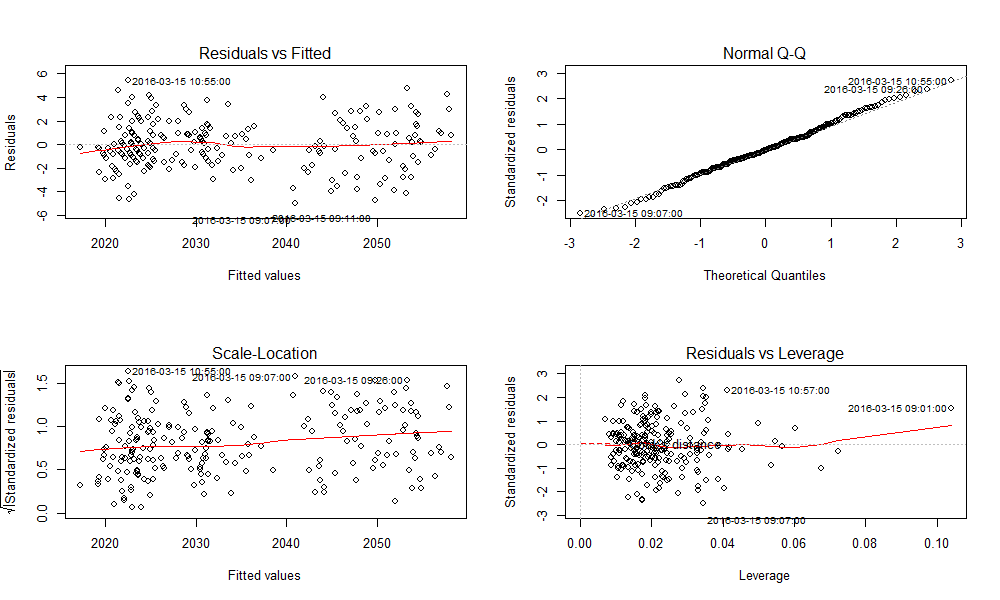
# 1. MATLAB线性拟合概述

MATLAB线性拟合是一种强大的技术，用于建立数据和线性函数之间的关系。它广泛应用于各种领域，包括工程、科学和金融。线性拟合的目标是找到一条直线或曲线，最能描述给定数据集中的数据点。

MATLAB提供了多种函数来执行线性拟合，包括`polyfit`和`fitlm`。这些函数允许用户指定拟合的阶数（直线或曲线）以及要使用的算法。通过线性拟合，用户可以预测新数据点、分析数据趋势并做出数据驱动的决策。

# 2. 线性拟合理论

**2.1 线性回归模型**

线性回归模型是一种统计模型，用于预测一个因变量（目标变量）与一个或多个自变量（预测变量）之间的线性关系。线性回归模型的方程形式为：

y = β0 + β1x1 + β2x2 + ... + βnxn + ε

其中：

* y 是因变量
* x1, x2, ..., xn 是自变量
* β0, β1, ..., βn 是模型参数
* ε 是误差项，表示模型与实际数据之间的差异

**2.2 最小二乘法**

最小二乘法是一种估计线性回归模型参数的方法。其目标是找到一组参数，使得模型预测值与实际值之间的平方误差最小。最小二乘法估计参数的公式为：

β = (X'X)^-1X'y

其中：

* X 是自变量矩阵
* y 是因变量向量
* β 是参数向量

**2.3 正则化方法**

正则化方法是一种通过向损失函数添加惩罚项来防止模型过拟合的技术。正则化项可以惩罚模型参数的大小或复杂性。常用的正则化方法包括：

* **L1正则化（LASSO）：** 惩罚参数的绝对值
* **L2正则化（岭回归）：** 惩罚参数的平方
* **弹性网络正则化：** L1 和 L2 正则化的组合

正则化项的超参数（例如，惩罚因子）可以通过交叉验证或其他技术来优化。

# 3.1 使用polyfit函数进行多项式拟合

**简介**

`polyfit` 函数是 MATLAB 中用于执行多项式拟合的强大工具。它使用最小二乘法算法来确定最佳拟合多项式，该多项式可以近似给定的数据点。本节将深入探讨 `polyfit` 函数的语法、参数和用法，并通过示例来说明如何使用它进行多项式拟合。

**语法**

p = polyfit(x, y, n)

**参数**

* `x`：一维向量，包含自变量的值。
* `y`：一维向量，包含因变量的值。
* `n`：拟合多项式的阶数。

**返回值**

* `p`：一个包含多项式系数的向量。多项式的最高次幂系数存储在向量的第一个元素中，依此类推。

**代码示例**

考虑以下数据点：

x = [1, 2, 3, 4, 5];
y = [2, 4, 8, 16, 32];

要拟合一个二次多项式（`n = 2`），可以使用以下代码：

p = polyfit(x, y, 2);

结果的 `p` 向量将包含二次多项式的系数：

p = [1, 2, 4]

这表示拟合多项式为：

y = 1 + 2x + 4x^2

**逻辑分析**

`polyfit` 函数通过最小化