MATLAB在信号处理中的应用：语音识别、噪声消除和频谱分析，信号处理的强大工具

# 1. MATLAB简介及信号处理基础

MATLAB 是一种强大的技术计算语言，广泛应用于工程、科学和金融等领域。它提供了一个交互式环境，用于数据分析、可视化和算法开发。

在信号处理方面，MATLAB 提供了一系列内置函数和工具箱，用于信号的获取、处理和分析。这些工具使工程师和研究人员能够高效地执行复杂的任务，例如信号滤波、特征提取和模式识别。

MATLAB 的信号处理基础包括数字信号表示、时域和频域分析。数字信号表示涉及将连续信号转换为离散形式，而时域分析和频域分析分别用于研究信号在时间和频率域中的特性。这些基础知识对于理解和处理信号至关重要，并为后续章节中更高级的信号处理技术奠定了基础。

# 2. MATLAB信号处理基础理论

### 2.1 信号的数字表示

#### 2.1.1 采样定理

采样定理规定，对于带宽为B的连续时间信号，其采样频率fs必须满足fs>=2B，才能保证信号在数字化后不失真。

#### 2.1.2 量化和编码

量化是将连续的模拟信号值转换为离散的数字值的过程，而编码是将量化后的数字值转换为二进制码的过程。量化误差和编码位数是量化和编码的重要指标。

### 2.2 信号的时域分析

#### 2.2.1 时域信号的特征

时域信号的特征包括幅度、频率、相位和持续时间。幅度表示信号的强度，频率表示信号的周期性，相位表示信号的起始点，持续时间表示信号的长度。

#### 2.2.2 时域信号的处理方法

时域信号的处理方法包括平滑、滤波、抽样和量化。平滑可以消除信号中的噪声，滤波可以提取信号中的特定频率成分，抽样可以将连续信号转换为离散信号，量化可以将模拟信号转换为数字信号。

### 2.3 信号的频域分析

#### 2.3.1 傅里叶变换

傅里叶变换是一种数学工具，可以将时域信号分解为一系列正弦波分量。傅里叶变换的幅度谱表示信号中每个频率分量的幅度，而相位谱表示信号中每个频率分量的相位。

#### 2.3.2 频域信号的特征

频域信号的特征包括频谱、带宽和功率谱密度。频谱表示信号中不同频率分量的分布，带宽表示信号中频率范围的宽度，功率谱密度表示信号中每个频率分量的功率。

% 采样定理示例
fs = 1000; % 采样频率
B = 500; % 信号带宽
if fs >= 2*B
    disp('满足采样定理')
else
    disp('不满足采样定理')
end

% 量化示例
x = linspace(0, 1, 100); % 模拟信号
y = round(x * 10) / 10; % 量化后的信号
figure;
plot(x, y, 'o');
title('量化示例');

% 时域信号处理示例
x = sin(2*pi*10*t) + 0.5*randn(size(t)); % 时域信号
y = smooth(x, 10); % 平滑后的信号
figure;
plot(t, x, 'b', t, y, 'r');
title('时域信号处理示例');

% 傅里叶变换示例
x = sin(2*pi*10*t); % 时域信号
X = fft(x); % 傅里叶变换
figure;
subplot(2, 1, 1);
plot(abs(X));
title('幅度谱');
subplot(2, 1, 2);
plot(angle(X));
title('相位谱');

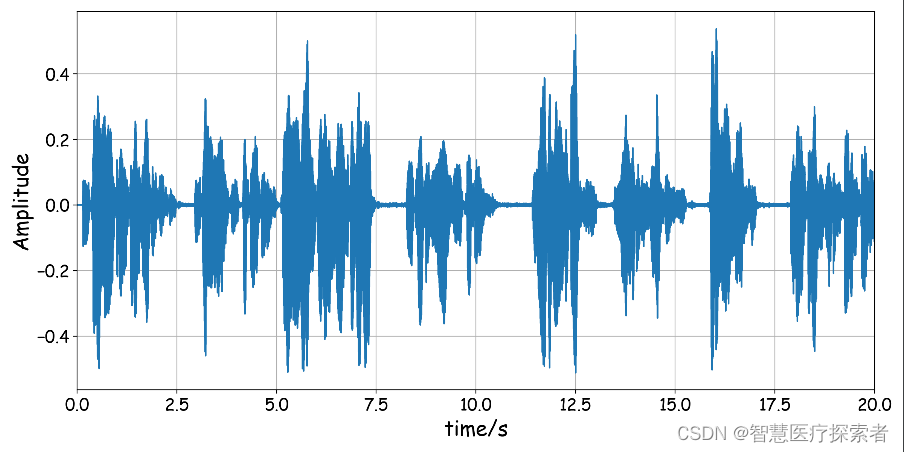
# 3.1 语音信号的特征提取

语音信号的特征提取是语音识别系统中的关键步骤，其目的是从原始语音信号中提取出能够有效区分不同语音单元（如音素、单词）的特征。