【MATLAB动态规划实现】：性能分析与高级应用

# 1. MATLAB动态规划基础

MATLAB (Matrix Laboratory) 是一款集数值计算、可视化以及编程于一体的高性能语言。在动态规划领域，MATLAB提供了丰富的数学工具箱以及强大的数值计算能力，非常适合动态规划问题的研究与解决。动态规划是一种解决多阶段决策问题的算法设计技术，具有最优子结构、重叠子问题等特性。MATLAB的矩阵运算和数组处理能力能够简化编程过程，提高开发效率。通过学习本章内容，读者可以掌握MATLAB动态规划的基本概念、编写简单的动态规划程序，并为下一章更深入的理论与算法学习打下坚实基础。

本章接下来将介绍如何在MATLAB中构建动态规划问题的基础框架，通过示例来展示动态规划的初步实现过程。我们将从一个简单的递归模型开始，逐步引导读者理解如何在MATLAB环境下实现动态规划算法，最终达到能够独立解决动态规划相关问题的水平。

# 2. MATLAB中的动态规划理论与算法

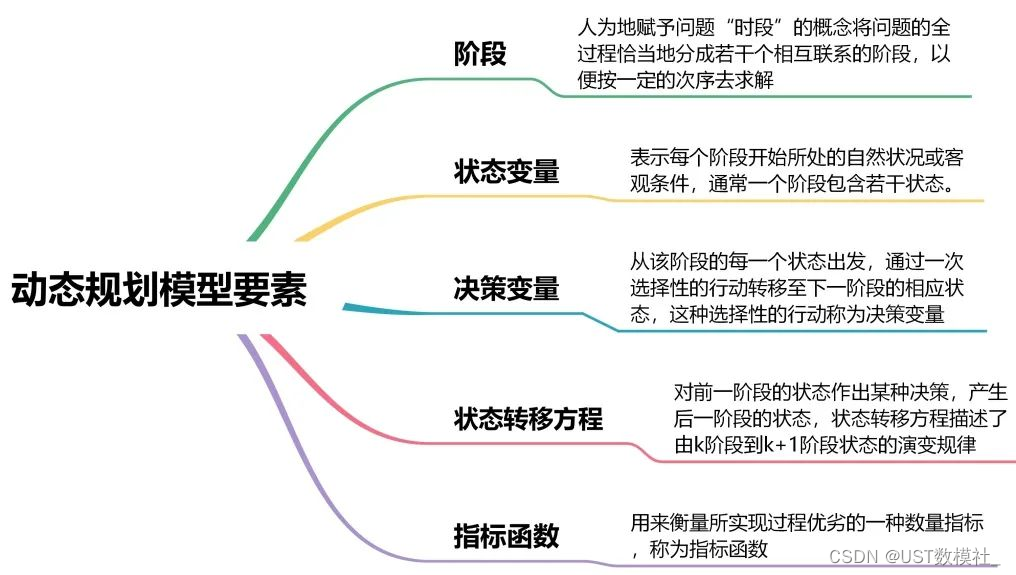
## 2.1 动态规划的基本原理

动态规划是一种解决多阶段决策过程优化问题的方法。在动态规划中，问题被分解为相互关联的子问题，并利用这些子问题的解来构建原问题的解。

### 2.1.1 最优子结构概念

最优子结构是指一个问题的最优解包含其子问题的最优解。换句话说，一个问题的全局最优解可以通过局部最优解的组合来得到。

### 2.1.2 状态转移方程的构建

状态转移方程是动态规划中非常核心的概念，用于描述问题状态之间的转换关系。具体来说，它表达了当前状态和前一状态之间的依赖关系。构建正确的状态转移方程是求解动态规划问题的关键。

## 2.2 典型问题的动态规划解法

### 2.2.1 背包问题的动态规划解法

背包问题是一类典型的组合优化问题。它描述的是在限定总重量的情况下，如何选择物品放入背包使得总价值最大。

% 假设有n种物品，每种物品的重量为w[i]，价值为v[i]，背包的最大承重为W
n = length(w); % 物品数量
W = 10; % 背包最大承重
dp = zeros(1, W+1); % 初始化动态规划表

for i = 1:n % 对每一种物品进行迭代
    for j = W:-1:w(i) % 从背包最大承重开始向下计算
        dp(j) = max(dp(j), dp(j-w(i))+v(i)); % 考虑放或不放物品i的情况，取较大值
    end
end

disp(dp(W)); % 输出最大价值

在上述代码中，`dp`数组用于记录每一个状态的最优解。数组的每个元素`dp(j)`表示背包容量为`j`时能够达到的最大价值。

### 2.2.2 最长公共子序列问题

最长公共子序列（LCS）问题是要找出两个序列共有的最长子序列。

% 假设有两个序列X和Y
X = 'AGGTAB';
Y = 'GXTXAYB';

% 构建LCS表
m = length(X);
n = length(Y);
L = zeros(m+1, n+1); % 初始化LCS表
for i = 1:m
    for j = 1:n
        if X(i) == Y(j)
            L(i+1, j+1) = L(i, j) + 1;
        else
            L(i+1, j+1) = max(L(i, j+1), L(i+1, j));
        end
    end
end

% L(m+1, n+1)即为LCS的长度
disp(L(m+1, n+1));

在这段代码中，二维数组`L`是状态转移表，它记录了序列`X`和`Y`的前`i`个和前`j`个字符的最长公共子序列的长度。

### 2.2.3 矩阵连乘问题

矩阵连乘问题是指给定一系列矩阵，求矩阵连乘乘积的计算顺序，使得乘法运算次数最少。

function cost = matrixChainOrder(p)
    % p为矩阵的维度数组，例如p=[30, 35, 15, 5, 10, 20, 25]
    n = length(p)-1; % 矩阵的数量
    m = zeros(1, n); % 初始化最小乘法次数数组
    s = zeros(1, n-1); % 初始化括号位置数组
    for i = 1:n
        m(i) = 0;
        s(i) = 0;
    end
    % 状态转移方程：m(i,j) = min(m(i,k) + m(k+1,j) + p(i-1)*p(k)*p(j)) for i <= k < j
    for l = 2:n % 子问题的长度
        for i = 1:n-l+1
            j = i+l-1;
            m(i,j) = inf;
            for k = i:j-1
                q = m(i,k) + m(k+1,j) + p(i-1)*p(k)*p(j);
                if q < m(i,j)
                    m(i,j) = q;
                    s(i,j) = k;
                end
            end
        end
    end
    cost = m(1,n); % 返回最小乘法次数
end

p = [30, 35, 15, 5, 10, 20, 25];
disp(matrixChainOrder(p));

在上述代码中，函数`matrixChainOrder`计算了给定矩阵链的最小乘法次数，`m(i,j)`记录了计算矩阵`i`到`j`的最小乘法次数，`s(i,j)`用于记录最优解的分割点。

## 2.3 动态规划中的高级技巧

### 2.3.1 状态压缩技术

状态压缩技术在处理某些动态规划问题时，特别是那些状态空间非常大的问题时，可以有效地减少内存的使用。

### 2.3.2 贪心策略与动态规划的结合

贪心策略与动态规划的结合是指在动态规划的某些步骤中使用贪心算法来简化问题的求解。

### 2.3.3 近似算法在动态规划中的应用

对于某些动态规划问题，可能没有精确解或者求解过程非常耗时，这时可以采用近似算法来获得一个可接受的近似解。

在下一章中，我们将具体探讨MATLAB动态规划实践技巧，包括编程环境的配置、编码实现和案例分析，以及性能分析等关键知识点。

# 3. MATLAB动态规划实践技巧

## 3.1 MATLAB编程环境配置

### 3.1.1 MATLAB开发工具介绍

MATLAB，作为一款由MathWorks公司开发的高性能数值计算和可视化软件，广泛应用于工程计算、控制系统设计、信号处理与通信、图像处理等众多领域。MATLAB提供了一种名为MATLAB Live Editor的交互式环境，它结合了代码编写、可视化以及文档编写于一体，极大地提高了程序员的开发效率。

开发工具方面，MATLAB集成了以下几项关键特性：
- 强大的数值计算能力，支持矩阵运算和函数运算。
- 高级图形工具和数据可视化功能。
- 高性能的图形处理单元（GPU）加速计算。
- 丰富的工具箱（Toolbox），涵盖从信号处理到深度学习等多个专业领域。
- 可扩展的算法开发环境，支持自定义函数和类库的开发。

在开始动态规划编码之前，推荐用户首先熟悉这些工具，并安装相应的开发工具包，这将为后续的开发工作打下坚实的基础。

### 3.1.2 MATLAB编程基础设置

在进行动态规划开发之前，对MATLAB环境进行基础设置是至关重要的。一些基础设置包括：
- **路径管理**：MATLAB的工作路径（Current Folder）决定了MATLAB会首先寻找哪些文件夹中的文件。调整路径设置，以方便快速访问常用的函数和脚本文件。
- **命令窗口选项**：可以调整命令窗口的历史记录、字体样式和大小等，以提高代码的可读性和操作的便捷性。
- **编辑器配置**：MATLAB编辑器支持代码折叠、代码高亮等高级编辑功能。适当配置这些选项可以提高编码效率。
- **内存管理**：在处理大数据集时，可以使用MATLAB提供的内存管理工具，如`clear`命令来释放不再使用的变量。
- **性能优化工具**：使用`profiler`工具分析代码性能瓶颈，以便进行优化。

## 3.2 MATLAB中动态规划的编码实现

### 3.2.1 MATLAB数组和矩阵操作技巧

MATLAB的核心是矩阵和数组操作，理解这些操作是编写高效动态规划代码的关键。动态规划通常涉及大量的矩阵运算，MATLAB对这类操作进行了优化，使其执行速度极快。以下是一些数组和矩阵操作的基础技巧：

1. **矩阵创建和初始化**：

   A = [1, 2; 3, 4]; % 创建一个2x2的矩阵
   v = 1:5; % 创建一个包含1到5的向量

2. **矩阵索引和子集操作**：

   A(2, :) % 获取矩阵A的第二行
   v(3:end) % 获取向量v从第三个元素到最后