【MATLAB神经网络优化】：理论与实践的完美结合

# 1. MATLAB神经网络基础

在这一章中，我们将探讨MATLAB神经网络的基础知识，为深入理解后续章节的进阶内容打下坚实的基础。MATLAB作为一种强大的数学计算和仿真工具，其在神经网络领域的应用同样显示出其卓越的性能。

## 1.1 MATLAB在神经网络中的作用

MATLAB提供了一系列用于神经网络设计、实现和应用的工具箱。其中，Neural Network Toolbox是专门用于神经网络设计和仿真的工具箱，它包含大量的函数和应用，可帮助研究人员和工程师在MATLAB环境中方便地构建和训练神经网络模型。借助MATLAB，我们可以直观地处理复杂的数据结构，实现高效的数值计算和结果的可视化展示。

## 1.2 神经网络的基本概念

神经网络是由大量的节点（或称神经元）相互连接构成的网络结构，通过模拟人脑神经元的工作方式，实现信息处理和学习功能。它由输入层、隐藏层（可能多个）和输出层组成，每一层由多个神经元构成。这些神经元通过连接权重相互作用，权重的调整是通过训练数据集来实现的。神经网络的基本学习过程包括前向传播和反向传播，通过不断的迭代，使得网络能够学习到输入和输出之间的复杂映射关系。

通过本章的学习，您将对神经网络的基本理论有一个全面的认识，并为下一章节关于神经网络设计与实现的深入探讨打下坚实的基础。

# 2. 神经网络的设计与实现

## 2.1 神经网络的结构

### 2.1.1 输入层、隐藏层和输出层的配置

神经网络的结构设计是实现特定功能的基础。在神经网络中，信息的处理是从输入层开始，经过隐藏层的层层处理，最终在输出层得到结果。每个层都是由一定数量的神经元组成，负责处理特定的输入数据。

**输入层**：这是网络接收外部输入数据的层次，输入层神经元的数量等于输入数据的特征数目。例如，在图像识别任务中，如果输入图像是28x28像素的灰度图，那么输入层就需要有28*28=784个神经元。

graph TD
    Input[输入层] --> Hidden1[隐藏层1]
    Hidden1 --> Hidden2[隐藏层2]
    Hidden2 --> Output[输出层]

**隐藏层**：隐藏层的神经元数量可以根据问题的复杂性进行调整。一般而言，隐藏层越多，网络的表达能力越强。但同时，过深的网络可能会导致难以训练的问题，比如梯度消失或梯度爆炸。

**输出层**：输出层的神经元数量取决于任务的类型。对于分类任务，输出层通常有与类别数目相同的神经元；对于回归任务，则通常只有一个神经元。

### 2.1.2 权值和阈值的作用与初始化

在神经网络中，每个神经元之间由权值连接，这些权值和阈值是网络训练学习的主要内容。权值决定了输入对神经元的影响强度，而阈值则确定了神经元激活的难度。

初始化权值和阈值对于网络性能的优劣有着重要影响。一个好的初始化方法可以加速网络的收敛，并避免梯度消失或爆炸的问题。常用的初始化方法有：

- **Xavier 初始化**：这种方法通过保持输入和输出的方差一致来避免梯度消失或爆炸。
- **He 初始化**：这是针对ReLU激活函数的改进型Xavier初始化，针对更深的网络特别有效。

初始化函数：
- Xavier: 使用`1 / sqrt(n)`来初始化权值，其中`n`为输入层神经元数目。
- He: 使用`2 / sqrt(n)`来初始化权值，其中`n`为输入层神经元数目。

初始化参数时，通常会随机赋予初始值，但初始化值的范围会根据方法不同而有所区别。

## 2.2 神经网络的学习算法

### 2.2.1 前馈传递与反向传播算法

神经网络通过前馈传递和反向传播算法来更新权值和阈值。在前馈传递过程中，输入数据被逐层处理，直到输出层产生结果。如果输出与期望值不符，就会通过反向传播算法计算误差，并更新网络参数。

反向传播算法的核心是链式法则，该法则用于计算损失函数对每个权值和阈值的梯度。梯度一旦被计算出来，就可以用梯度下降法来更新网络参数，从而减少损失。

# 伪代码示例，展示了反向传播算法的基本步骤
def backward_pass():
    # 计算输出层误差
    output_error = calculate_output_error()
    # 反向传播误差，计算隐藏层梯度
    hidden_layer_gradients = calculate_hidden_layer_gradients(output_error)
    # 更新权重和阈值
    update_weights_and_biases(hidden_layer_gradients)

参数更新是通过一个学习率来控制的，学习率决定了参数更新的步长。学习率过小会导致学习过程缓慢，过大则可能导致网络震荡不收敛。

### 2.2.2 梯度下降法及其变体

梯度下降法是训练神经网络最基础的算法。它通过计算损失函数对参数的梯度，然后沿着下降最快的方向更新参数。梯度下降有多种变体，包括批量梯度下降、随机梯度下降（SGD）和小批量梯度下降。

- **批量梯度下降**：一次计算整个训练集的平均梯度并更新参数。这种方法的计算量大，但比较稳定。
- **随机梯度下降（SGD）**：每次只用一个样本点来更新参数，这种方法的随机性较大，但能够快速地接近最小值。
- **小批量梯度下降**：介于两者之间，每次使用一小批样本来更新参数。这种方法结合了两者的优点。

# 使用随机梯度下降（SGD）的代码示例
def stochastic_gradient_descent(loss_function, parameters, learning_rate, batch_size):
    for epoch in range(number_of_epochs):
        for batch in get_minibatches(data, batch_size):
            gradients = compute_gradients(loss_function, batch, parameters)
            parameters = apply_gradients(parameters, gradients, learning_rate)
    return parameters

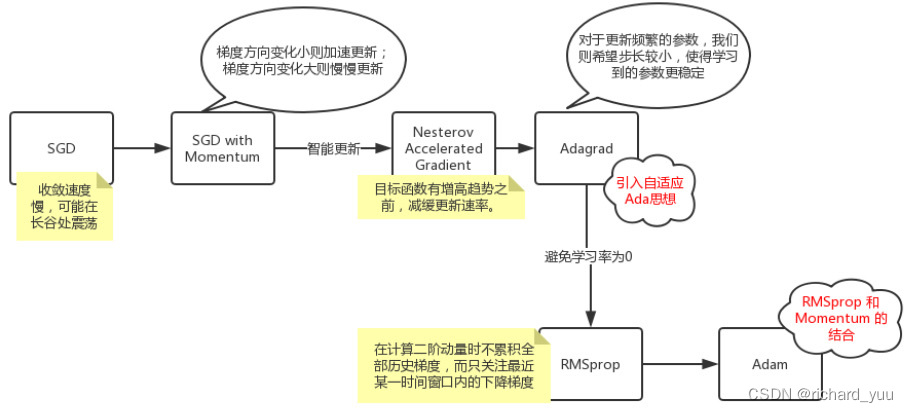
为了优化SGD，还引入了动量（Momentum）和自适应学习率算法如Adagrad、RMSprop和Adam等。

### 2.2.3 自适应学习率的策略

自适应学习率算法能够根据学习过程中的情况自动调整学习率，使得网络的训练更加高效。Adam算法是目前最流行的自适应学习率算法之一。

Adam算法综合了RMSprop和动量的概念，不仅保存了过去梯度的一阶矩估计（即动量），也保存了过去梯度的二阶矩估计，从而实现对学习率的动态调整。

# Adam优化器的伪代码示例
def adam_optimizer(parameters, gradients, learning_rate, beta1, beta2, epsilon):
    # 初始化一阶和二阶矩估计变量
    first_moment = zeros_like(parameters)
    second_moment = zeros_like(parameters)
    for t in range(number_of_iterations):
        # 更新一阶和二阶矩估计
        first_moment = beta1 * first_moment + (1 - beta1) * gradients
        second_moment = beta2 * second_moment + (1 - beta2) * gradients**2
        # 根据一阶和二阶矩估计调整学习率
        first_moment_unbiased = first_moment / (1 - beta1**(t+1))
        second_moment_unbiased = second_moment / (1 - beta2**(t+1))
        parameters = parameters - learning_rate * first_moment_unbiased / (sqrt(second_moment_unbiased) + epsilon)
    return parameters

## 2.3 神经网络的训练与验证

### 2.3.1 训练数据集的准备与划分

神经网络的训练开始于对数据集的准备。一个典型的数据集通常被划分为训练集、验证集和测试集三个部分。训练集用于训练模型，验证集用于调优模型参数，测试集用于最终评估模型的性能。

划分数据集的常用方法有：

- **随机划分**：数据被随机分配到各个集合中，适用于数据量大且分布均匀的情况。
- **K折交叉验证**：数据被划分为K个互斥的子集，每个子集轮流作为验证集，其余作为训练集。这种方法可以更充分地利用有限的数据。

例如，使用Python的sklearn库划分数据集：

from sklearn.model_selection import train_test_split

# 假设X为特征数据，y为目标值
X_train, X_temp, y_train, y_temp = train_test_split(X, y, test_size=0.3, random_state=42)
X_val, X_test, y_val, y_test = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42)

### 2.3.2 网络性能的评估指标

评估指标是用来衡量模型性能好坏的标准，不同的问题类型对应不同的评估指标。常见的评估指标有：

- **准确率（Accuracy）**：正确分类的样本数占总样本数的比例。
- **精确率（Precision）**：正确预测为正的样本数占预测为正的样本数的比例。
- **召回率（Recall）**：正确预测为正的样本数占实际为正的样本数的比例。
- **F1分数**：精确率和召回率的调和平均数。

评估函数示例：

def calculate_metrics(y_true, y_pred):
    accuracy = accuracy_score(y_true, y_pred)
    precision = precision_score(y_true, y_pred)
    recall = recall_score(y_true, y_pred)
    f1 = f1_score(y_true, y_pred)
    return accuracy, precision, recall, f1

### 2.3.3 过拟合与欠拟合的处理方法

在训练过程中，模型可能会出现过拟合或欠拟合的现象。过拟合是指模型在训练集上表现很好，但在验证集或测试集上表现差；欠拟合则是指模型在训练集上的表现就很差。

**过拟合的处理方法**：

- **早停法**：在验证集上监控性能，当性能不再提高时停止训练。
- **正则化**：通过增加L1或L2项到损失函数中，惩罚大的权重值，限制模型复杂度。
- **数据增强**：增加训练数据集的多样性，减少模型对训练数据的依赖。

例如，使用L2正则化的代码示例：

def l2_regularized_loss(loss_function, parameters, lambda):
regularization_loss = 0
for param in par