堆在系统设计中的核心地位：面向架构师的权威解读

# 1. 堆在系统设计中的重要性**

堆是一种高效的数据结构，在系统设计中扮演着至关重要的角色。它是一种基于二叉树的结构，具有快速插入、删除和查找最小（或最大）元素的特性。

堆的优势在于其时间复杂度低，插入和删除操作的时间复杂度为 O(log n)，查找最小（或最大）元素的时间复杂度为 O(1)。这使得堆非常适合需要快速处理大量数据的系统。

在系统设计中，堆广泛应用于内存管理、数据库、并发编程和分布式系统等领域。通过利用堆的特性，系统可以提高性能、优化资源分配和实现高效的并发处理。

# 2.1 堆的数据结构和算法

### 2.1.1 二叉堆和优先队列

堆是一种完全二叉树，满足以下性质：

- **堆序性：**每个节点的值都大于或等于其子节点的值。
- **完全性：**除最后一层外，每一层都填满。

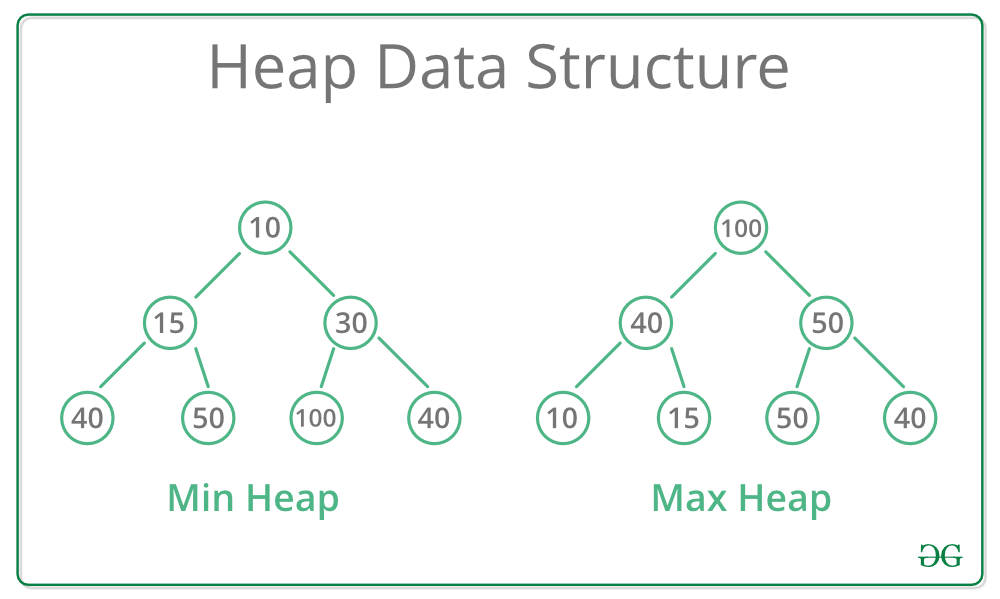
二叉堆可以分为两种类型：

- **最大堆：**根节点的值最大。
- **最小堆：**根节点的值最小。

优先队列是一种抽象数据类型，它支持以下操作：

- `insert(x)`：将元素 `x` 插入队列。
- `extract_min()`：删除并返回队列中最小的元素。
- `peek()`：返回队列中最小的元素而不删除它。

二叉堆是一种实现优先队列的有效数据结构。

### 2.1.2 堆的构建和维护

**构建堆：**

给定一个无序数组，可以通过自底向上的方式构建一个堆。

def build_heap(arr):
    n = len(arr)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, i, n)

**维护堆：**

当插入或删除元素时，需要维护堆的堆序性。

**插入元素：**

1. 将元素插入到数组的末尾。
2. 从末尾节点开始，与父节点比较，如果父节点的值小于当前节点的值，则交换它们。
3. 重复步骤 2，直到到达根节点或父节点的值大于当前节点的值。

**删除元素：**

1. 将根节点的值替换为数组中最后一个元素。
2. 删除数组中的最后一个元素。
3. 从根节点开始，与较大的子节点比较，如果子节点的值大于当前节点的值，则交换它们。
4. 重复步骤 3，直到到达叶子节点或较大的子节点的值小于当前节点的值。

def heapify(arr, i, n):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[left] > arr[largest]:
        largest = left

    if right < n and arr[right] > arr[largest]:
        largest = right

    if largest != i: