堆的比拼：二叉堆、斐波那契堆和左式堆

# 1. 堆的概述

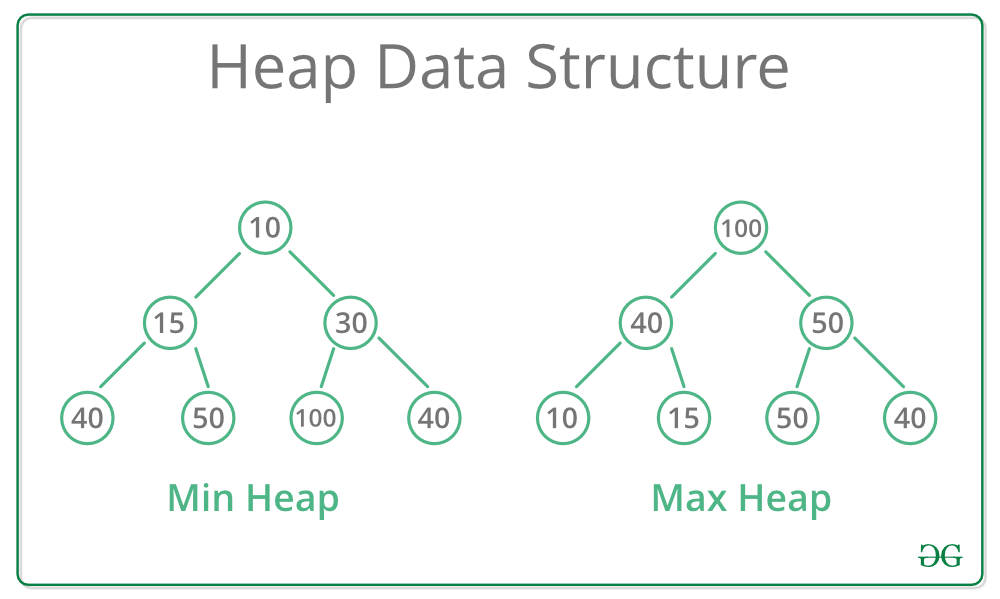
堆是一种特殊的树形数据结构，它满足以下性质：

- **完全二叉树：**堆是一棵完全二叉树，即除了最后一层外，所有层都被完全填充。
- **堆序性质：**堆中每个节点的值都小于或等于其子节点的值。

堆具有以下优点：

- **快速插入和删除：**在堆中插入或删除元素的时间复杂度为 O(log n)。
- **高效查找：**堆的根节点始终是堆中最小或最大的元素，因此查找最大或最小值的时间复杂度为 O(1)。

# 2. 二叉堆

### 2.1 二叉堆的性质和操作

#### 2.1.1 二叉堆的定义和表示

**定义：**

二叉堆是一种完全二叉树，满足以下性质：

* **最小堆：**每个节点的值都小于或等于其子节点的值。
* **最大堆：**每个节点的值都大于或等于其子节点的值。

**表示：**

二叉堆通常使用数组表示，其中：

* 根节点位于数组的第一个元素（索引为 0）。
* 左子节点位于索引为 `2 * i + 1` 的元素。
* 右子节点位于索引为 `2 * i + 2` 的元素。

#### 2.1.2 二叉堆的插入和删除

**插入：**

1. 将新元素添加到数组末尾。
2. 与其父节点比较，如果违反堆性质，则交换元素位置。
3. 重复步骤 2，直到达到根节点或堆性质得到满足。

def insert(heap, element):
    """
    插入一个元素到二叉堆中。

    Args:
        heap (list): 二叉堆。
        element: 要插入的元素。
    """
    heap.append(element)
    i = len(heap) - 1
    while i > 0:
        parent = (i - 1) // 2
        if heap[i] < heap[parent]:
            heap[i], heap[parent] = heap[parent], heap[i]
        i = parent

**删除：**

1. 将根节点替换为数组最后一个元素。
2. 将数组最后一个元素删除。
3. 与其较小的子节点比较，如果违反堆性质，则交换元素位置。
4. 重复步骤 3，直到达到叶子节点或堆性质得到满足。

def delete(heap):
    """
    从二叉堆中删除根节点。

    Args:
        heap (list): 二叉堆。
    """
    if not heap:
        return

    heap[0] = heap[-1]
    heap.pop()
    i = 0
    while i < len(heap):
        left = 2 * i + 1
        right = 2 * i + 2
        if left < len(heap) and heap[left] < heap[i]:
            heap[i], heap[left] = heap[left], heap[i]
            i = left
        elif right < len(heap) and heap[right] < heap[i]:
            heap[i], heap[right] = heap[right], heap[i]
            i = right
        else:
            break

### 2.2 二叉堆的应用

#### 2.2.1 排序算法

二叉堆可以用于实现堆排序算法。堆排序是一种非递归的排序算法，时间复杂度为 O(n log n)。

**步骤：**

1. 将输入数组构建成一个最大堆。
2. 从堆中删除根节点（最大元素），并将其放置在数组末尾。
3. 将剩余的堆重新调整为最大堆。
4. 重复步骤 2 和 3，直到堆为空。

#### 2.2.2 优先队列

二叉堆可以用于实现优先队列数据结构。优先队列是一种支持以下操作的数据结构：

* `inse