算法与数据结构：从基础到高级，掌握100个必知算法和数据结构

# 1. 算法与数据结构概述

算法是解决特定问题的步骤序列，而数据结构是组织和存储数据的有效方式。算法和数据结构是计算机科学的基础，它们在软件开发、数据分析和人工智能等领域有着广泛的应用。

算法的效率由其时间复杂度和空间复杂度衡量。时间复杂度描述算法执行所需的时间，而空间复杂度描述算法执行所需的空间。算法设计范式，如贪心算法、分治算法和动态规划，提供了解决常见问题的有效方法。

# 2. 算法基础

### 2.1 算法的时间复杂度分析

#### 2.1.1 大O表示法

大O表示法是一种用于描述算法时间复杂度的渐近上界。它表示随着输入规模趋于无穷大时，算法运行时间相对于输入规模的增长速度。大O表示法使用以下符号：

O(f(n))

其中：

* `n` 是输入规模
* `f(n)` 是算法运行时间相对于 `n` 的增长率

例如，如果一个算法的时间复杂度为 O(n^2)，则表示算法的运行时间随着输入规模的平方而增长。

#### 2.1.2 常用时间复杂度类别

以下是常见的算法时间复杂度类别：

| 类别 | 表示法 | 增长率 |
|---|---|---|
| 常数 | O(1) | 不随输入规模增长 |
| 线性 | O(n) | 与输入规模成正比 |
| 平方 | O(n^2) | 与输入规模的平方成正比 |
| 立方 | O(n^3) | 与输入规模的立方成正比 |
| 对数 | O(log n) | 与输入规模的对数成正比 |
| 指数 | O(2^n) | 与输入规模的指数成正比 |

### 2.2 算法的空间复杂度分析

#### 2.2.1 空间复杂度度量

算法的空间复杂度度量算法在运行过程中所占用的内存空间。它表示算法在运行时所需的辅助存储空间，不包括输入和输出数据所占用的空间。

#### 2.2.2 常见空间复杂度类别

以下是常见的算法空间复杂度类别：

| 类别 | 表示法 | 占用空间 |
|---|---|---|
| 常数 | O(1) | 不随输入规模增长 |
| 线性 | O(n) | 与输入规模成正比 |
| 平方 | O(n^2) | 与输入规模的平方成正比 |
| 立方 | O(n^3) | 与输入规模的立方成正比 |
| 对数 | O(log n) | 与输入规模的对数成正比 |

### 2.3 算法设计范式

算法设计范式是指导算法设计的通用方法。以下是一些常见的算法设计范式：

#### 2.3.1 贪心算法

贪心算法是一种逐个做出局部最优选择，最终得到全局最优解的算法。它适用于具有以下特征的问题：

* 局部最优解可以有效地计算
* 局部最优解可以组合成全局最优解

#### 2.3.2 分治算法

分治算法是一种将问题分解成更小的子问题，递归地解决子问题，然后合并子问题的解以得到原始问题的解的算法。它适用于具有以下特征的问题：

* 问题可以分解成更小的子问题
* 子问题可以独立解决
* 子问题的解可以合并成原始问题的解

#### 2.3.3 动态规划

动态规划是一种通过将问题分解成重叠子问题，并存储子问题的解来避免重复计算的算法。它适用于具有以下特征的问题：

* 问题可以分解成重叠子问题
* 子问题的解可以存储和重用
* 子问题的解可以组合成原始问题的解

# 3. 数据结构基础

### 3.1 数组和链表

#### 3.1.1 数组的特性和应用

数组是一种线性数据结构，其中元素按顺序存储在连续的内存位置中。每个元素都有一个唯一的索引，可以用来访问它。数组具有以下特性：

- **快速访问：**由于元素存储在连续的内存中，因此可以通过索引快速访问任何元素。
- **插入和删除效率低：**在数组中间插入或删除元素需要移动所有后续元素，这可能会很慢，尤其是对于大型数组。
- **固定大小：**数组的大小在创建时确定，并且不能动态更改。

数组通常用于存储大量同类型的数据，例如数字、字符串或对象。它们特别适用于需要快速随机访问元素的情况。

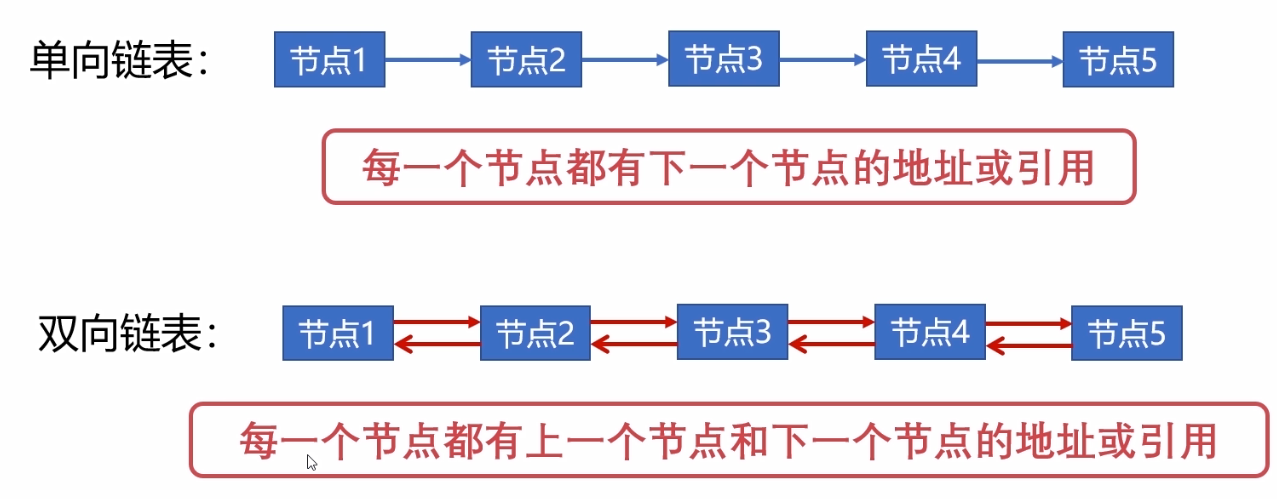
#### 3.1.2 链表的特性和应用

链表是一种线性数据结构，其中元素存储在分散的内存位置中。每个元素包含一个数据项和指向下一个元素的指针。链表具有以下特性：

- **动态大小：**链表可以动态增长或缩小，以适应存储的数据量。
- **插入和删除效率高：**在链表中插入或删除元素只需要更新指针，而不需要移动其他元素。
- **顺序访问慢：**访问链表中的元素需要从头开始遍历整个链表，这可能会很慢，尤其是对于大型链表。

链表通常用于存储不规则大小或需要频繁插入和删除元素的数据。它们特别适用于需要顺序访问元素的情况。

### 3.2 栈和队列

#### 3.2.1 栈的特性和应用

栈是一种线性数据结构，遵循后进先出 (LIFO) 原则。元素按顺序添加到栈的顶部，并且只能从顶部删除。栈具有以下特性：

- **后进先出：**后添加到栈中的元素将首先被删除。
- **快速插入和删除：**在栈中插