【数据结构选型秘籍】：在Codeforces中如何精准选择数据结构

# 1. 数据结构的基本概念与在算法竞赛中的重要性

数据结构是算法竞赛中不可或缺的一部分，它不仅是编写有效算法的基础，而且能够帮助我们更好地理解问题并设计出更优的解决方案。在这一章中，我们将介绍数据结构的基本概念，并探讨它在算法竞赛中扮演的关键角色。

## 1.1 数据结构的定义

数据结构是计算机存储、组织数据的方式，它能够帮助我们高效地执行数据操作（如访问、搜索、插入和删除）。在算法竞赛中，它的重要性不言而喻，因为它直接影响到我们解决问题的效率。

## 1.2 数据结构的重要性

在算法竞赛中，一个优秀的数据结构能够为问题解决提供清晰的思路和高效的执行路径。掌握多种数据结构，可以让我们在面对不同类型的题目时，有更多选择，从而达到优化时间和空间复杂度的目的。

## 1.3 如何学习数据结构

学习数据结构不仅需要记忆其定义和操作方法，更重要的是要理解其背后的原理，以及在不同问题中的应用场景。通过实际编写代码来实现各种数据结构，并在算法练习中尝试应用，能够加深我们对其理解和应用能力。

以上内容简要介绍了数据结构的基本概念以及它在算法竞赛中的重要性，为后续章节中详细介绍不同数据结构和应用场景奠定了基础。

# 2. 线性数据结构及其应用

## 2.1 线性数据结构概述

### 数组与链表的对比分析

线性数据结构是最基本的数据结构之一，包括数组(Array)和链表(LinkedList)。它们是构建更复杂数据结构的基石，因此理解它们的原理和性能特点是关键。

数组是一种存储固定大小的相同类型元素的数据结构。数组允许通过索引快速访问元素，其时间复杂度为O(1)，但在添加或删除元素时可能需要移动大量元素，时间复杂度为O(n)。而链表由一系列节点组成，每个节点包含数据和指向下一个节点的引用。链表允许动态大小，插入和删除操作相对高效，但访问元素需要遍历整个列表，时间复杂度为O(n)。

在实际应用中，选择数组还是链表取决于具体需求。例如，如果需要频繁访问元素，数组可能是更好的选择；如果应用场景中需要频繁地插入或删除元素，链表可能更加合适。

### 栈与队列的原理及实现

栈(Stack)和队列(Queue)是两种特殊的线性数据结构，它们都有一系列操作，但各自的行为却大不相同。

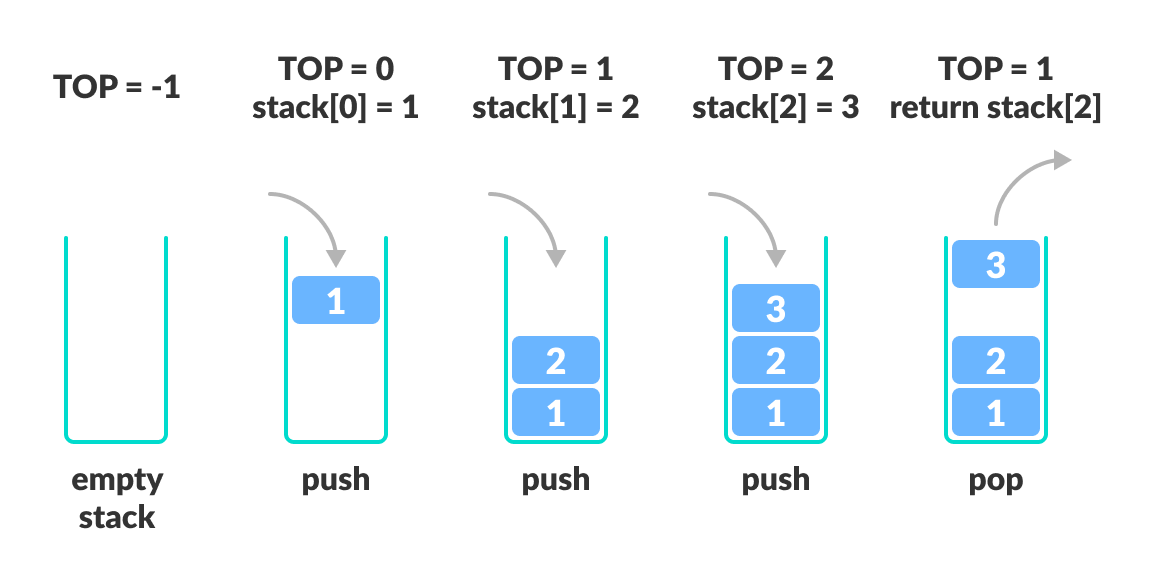
栈是一种后进先出（LIFO）的数据结构，支持两种基本操作：压栈（push）和弹栈（pop）。栈允许在栈顶进行添加和移除元素操作，因此最后一个进入栈的数据元素将是第一个被弹出的。栈的实现可以使用数组也可以使用链表。例如，使用数组实现的栈可以这样定义：

class Stack:
    def __init__(self):
        self.items = []

    def is_empty(self):
        return len(self.items) == 0

    def push(self, item):
        self.items.append(item)

    def pop(self):
        if not self.is_empty():
            return self.items.pop()
        return None

队列是一种先进先出（FIFO）的数据结构，主要操作有入队（enqueue）和出队（dequeue）。队列允许在队尾添加元素，并从队头移除元素。队列也可以用数组或链表实现。以下是使用链表实现的一个简单队列：

class Node:
    def __init__(self, value):
        self.value = value
        self.next = None

class Queue:
    def __init__(self):
        self.front = None
        self.rear = None

    def is_empty(self):
        return self.front is None

    def enqueue(self, item):
        new_node = Node(item)
        if self.rear is None:
            self.front = self.rear = new_node
        else:
            self.rear.next = new_node
            self.rear = new_node

    def dequeue(self):
        if self.is_empty():
            return None
        removed = self.front.value
        self.front = self.front.next
        if self.front is None:
            self.rear = None
        return removed

栈和队列在算法和编程中有广泛的应用，如用于算法中的函数调用栈、深度优先搜索(DFS)、广度优先搜索(BFS)等。

## 2.2 动态数组与字符串处理

### 动态数组的扩展机制

动态数组是一种动态调整大小的数组，例如Python中的`list`类型，允许在运行时根据需要扩展数组容量。动态数组的扩展机制通常涉及重新分配内存并复制现有元素到新的内存空间。大多数现代语言的动态数组通过加倍策略来优化性能。

例如，当动态数组达到当前容量限制时，它会扩展到原来的两倍容量，这确保了摊销后的插入操作的时间复杂度接近O(1)。Python的列表实现使用了加倍策略，且当收缩时也会减少容量。

# Python列表实现示例
my_list = [1, 2, 3]
my_list.append(4)  # 在末尾添加元素，如果需要则扩展数组

### 字符串匹配与处理技巧

字符串匹配是处理文本数据的基础操作。例如，寻找一个子串在一个字符串中出现的所有位置，或反转一个字符串等。字符串处理的算法复杂度可以从线性时间复杂度（如KMP算法）到二次时间复杂度（如朴素字符串匹配）不等。

字符串反转的简单实现，例如在Python中，可以使用以下方式：

def reverse_string(s):
    return s[::-1]  # 利用Python的切片操作实现字符串反转

处理字符串时常用的数据结构包括前缀树（Trie）、后缀树、动态规划等。例如，后缀数组和后缀树可以用于高效的字符串搜索和匹配。

## 2.3 栈和队列的实际应用

### 深度优先搜索(DFS)与栈的结合

深度优先搜索(DFS)是一种用于遍历或搜索树或图的算法。DFS使用栈来保存将要访问的节点的列表。

DFS的典型实现使用递归方法，但也可以使用栈实现非递归版本。在非递归版本中，访问一个节点后，将其所有未访问的邻接节点推入栈中。例如，下面是一个使用栈实现的DFS遍历图的算法：

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    stack = [start]
    while stack:
        vertex = stack.pop()
        if vertex not in visited:
            print(vertex)  # 处理节点
            visited.add(vertex)