BP神经网络预测局部最优问题：深入分析与彻底解决

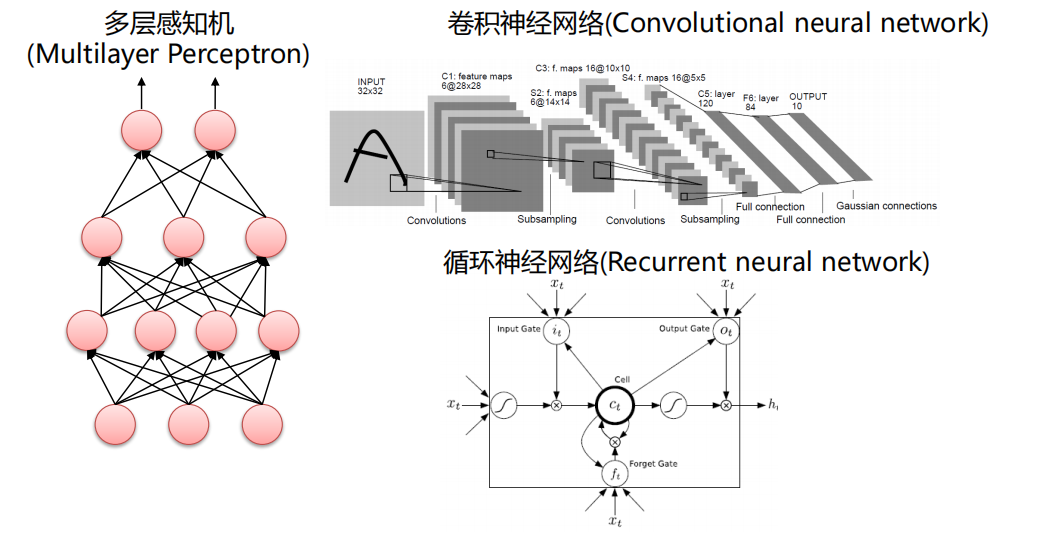
# 1. BP神经网络基本原理**

**1.1 BP神经网络概述**

BP神经网络（反向传播神经网络）是一种多层前馈神经网络，它通过反向传播算法来学习和调整网络权重，以最小化目标函数。BP神经网络由输入层、隐含层和输出层组成，其中隐含层可以有多层。

**1.2 BP神经网络的学习算法**

BP神经网络的学习算法包括以下步骤：

* **前向传播：**将输入数据通过网络层层传递，得到输出。
* **计算误差：**计算输出与目标之间的误差。
* **反向传播：**将误差反向传播到网络中，计算每个权重的梯度。
* **更新权重：**根据梯度和学习率更新网络权重。

# 2. BP神经网络预测局部最优问题

### 2.1 局部最优问题概述

**局部最优问题**是指在优化过程中，算法陷入局部最优解，无法找到全局最优解。局部最优解是一个局部范围内最优的解，但不是整个搜索空间中的最优解。

在BP神经网络预测中，局部最优问题表现为预测误差无法进一步降低，尽管网络已经经过多次训练迭代。这可能是由于网络陷入了一个局部最优解，该解不是全局最优解。

### 2.2 BP神经网络预测中的局部最优问题

BP神经网络预测中的局部最优问题主要由以下因素引起：

- **非凸损失函数：**BP神经网络预测中常用的损失函数，如均方误差和交叉熵，通常是非凸的。这使得优化过程可能陷入局部最优解。
- **高维参数空间：**BP神经网络通常具有大量参数，这增加了搜索局部最优解的可能性。
- **过拟合：**当网络过度拟合训练数据时，可能会陷入局部最优解，该解在训练数据上表现良好，但在新数据上表现不佳。

### 2.3 局部最优问题的解决策略

解决BP神经网络预测中的局部最优问题，可以采用以下策略：

- **动量法：**动量法通过引入动量项来加速优化过程，并防止算法陷入局部最优解。
- **自适应学习率：**自适应学习率算法根据训练过程中梯度的变化动态调整学习率，从而避免算法陷入局部最优解。
- **正则化：**正则化通过向损失函数添加正则化项来防止过拟合，从而减少局部最优解的可能性。
- **权重衰减：**权重衰减是一种正则化技术，通过对网络权重施加惩罚来防止过拟合，从而减少局部最优解的可能性。

# 3. 局部最优问题的解决策略

### 3.1 动量法

**原理：**

动量法通过引入动量项，在更新权重时考虑了前一次迭代的梯度方向，从而使权重更新更加平滑，减少震荡，有利于跳出局部最优。

**公式：**

v_t = β * v_{t-1} + (1 - β) * ∇L(w_{t-1})
w_t = w_{t-1} - α * v_t

其中：

* `v_t` 为动量项
* `β` 为动量系数，一般取值在 0.5 到 0.9 之间
* `α` 为学习率
* `∇L(w_{t-1})` 为损失函数对权重 `w_{t-1}` 的梯度

**参数说明：**

* `β`：控制动量项对当前梯度的平滑程度，值越大，平滑效果越明显。
* `α`：控制权重更新的步长，值越大，更新越快。

**代码块：**

import numpy as np

def momentum_update(w, grad, v, beta, alpha):
  """
  动量法更新权重

  Args:
    w: 当前权重
    grad: 梯度
    v: 动量项
    beta: 动量系数
    alpha: 学习率

  Returns:
    更新后的权重
  """

  v = beta * v + (1 - beta) * grad
  w = w - alpha * v
  return w

**逻辑分析：**

该代码实现了动量法更新权重的过程。首先计算动量项 `v`，然后根据动量项和学习率更新权重 `w`。

### 3.2 自适应学习率

**原理：**

自适应学习率通过动态调整学习率，在不同训练阶段使用不同的学习率。在训练初期，使用较大的学习率加速收敛；在训练后期，使用较小的学习率精细调整权重，避免过拟合。

**公式：**

α_t = α_0 / (1 + α_0 * ∑_{i=1}^t ||∇L(w_i)||^2)

其中：

* `α_t` 为第 `t` 次迭代的学习率
* `α_0` 为初始学习率
* `∇L(w_i)` 为第 `i` 次迭代的梯度

**参数说明：**

* `α_0`：初始学习率，控制学习率调整的幅度。
* `∑_{i=1}^t ||∇L(w_i)||^2`：梯度平方和，反映了训练过程的平滑程度。

**代码块：**

im