BP神经网络预测损失函数：选择与优化，提升模型准确度

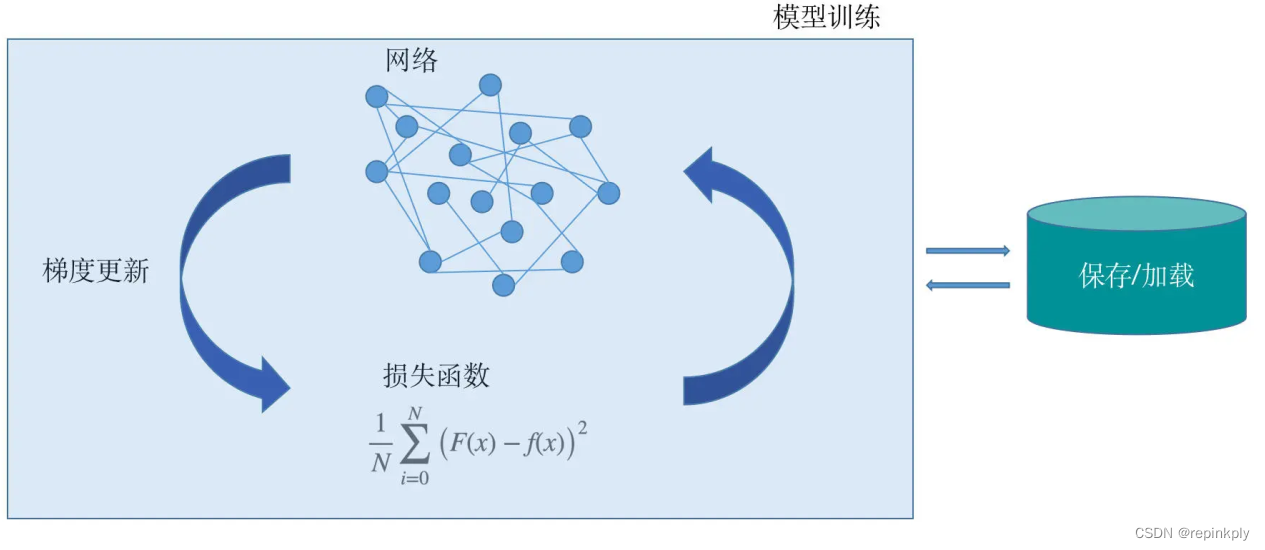
# 1. BP神经网络简介

BP神经网络（反向传播神经网络）是一种多层前馈神经网络，以其强大的非线性拟合能力而闻名。它由输入层、隐含层和输出层组成，其中隐含层可以有多个。BP神经网络通过反向传播算法训练，该算法通过计算输出层和目标值之间的误差，并将其反向传播到网络中，从而调整网络权重和偏置。

# 2. BP神经网络的损失函数

### 2.1 损失函数的类型

损失函数衡量神经网络预测值与真实值之间的差异，是神经网络训练过程中优化目标。常见的损失函数类型包括：

#### 2.1.1 平方误差损失函数

平方误差损失函数计算预测值与真实值之间的平方差，公式如下：

L(y, y_hat) = 1/2 * ||y - y_hat||^2

其中：

* `y` 为真实值
* `y_hat` 为预测值

平方误差损失函数简单易懂，但对异常值敏感，容易导致梯度爆炸。

#### 2.1.2 交叉熵损失函数

交叉熵损失函数衡量预测概率分布与真实概率分布之间的差异，公式如下：

L(y, y_hat) = -y * log(y_hat) - (1 - y) * log(1 - y_hat)

其中：

* `y` 为真实标签（0 或 1）
* `y_hat` 为预测概率

交叉熵损失函数对异常值不敏感，适用于二分类问题。

### 2.2 损失函数的选择

#### 2.2.1 不同损失函数的优缺点

| 损失函数 | 优点 | 缺点 |
|---|---|---|
| 平方误差损失函数 | 简单易懂 | 对异常值敏感 |
| 交叉熵损失函数 | 对异常值不敏感 | 适用于二分类问题 |

#### 2.2.2 损失函数的选择原则

损失函数的选择应考虑以下原则：

* **任务类型：**不同任务类型（如回归、分类）需要不同的损失函数。
* **数据分布：**损失函数应与数据分布相匹配，避免对异常值过于敏感。
* **模型复杂度：**复杂模型可能需要更鲁棒的损失函数，以防止梯度爆炸或消失。

# 3. BP神经网络的损失函数优化

### 3.1 梯度下降法

#### 3.1.1 梯度下降法的原理

梯度下降法是一种迭代优化算法，用于最小化损失函数。其基本思想是沿着损失函数梯度的负方向更新模型参数，使得损失函数不断减小。

#### 3.1.2 梯度下降法的算法

梯度下降法的算法如下：

# 初始化模型参数
w = w0

# 迭代优化
while not converged:
    # 计算损失函数的梯度
    g = ∇L(w)

    # 更新模型参数