拟合函数误差分析：评估模型准确性的3个关键指标

# 1. 拟合函数误差分析概述

拟合函数误差分析是评估机器学习模型性能的关键步骤。它涉及量化模型预测与真实值之间的差异，以了解模型的准确性和泛化能力。误差分析有助于识别模型的不足之处，指导模型改进策略，并为模型选择和部署提供信息。

在拟合函数误差分析中，通常使用各种指标来评估模型的性能。这些指标包括均方误差（MSE）、平均绝对误差（MAE）和根均方误差（RMSE）。每个指标都有其优点和缺点，在不同的场景下适用。通过分析这些指标，我们可以深入了解模型的预测能力，并为模型的优化和部署做出明智的决策。

# 2. 拟合函数误差评估指标

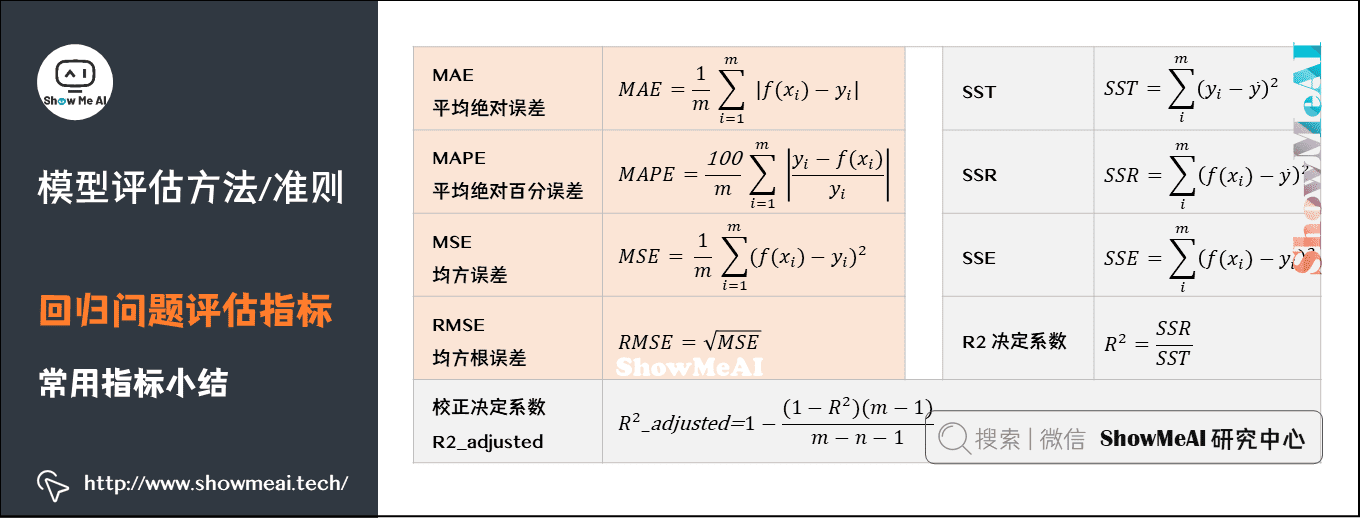
拟合函数误差评估指标是衡量拟合函数性能的重要工具，用于量化模型预测与真实值之间的差异。常用的误差评估指标包括均方误差（MSE）、平均绝对误差（MAE）和根均方误差（RMSE）。

### 2.1 均方误差（MSE）

**2.1.1 MSE的定义和计算**

均方误差（MSE）是预测值与真实值之间平方差的平均值，计算公式为：

MSE = (1/n) * Σ(y_i - y_hat_i)^2

其中：

* n 为样本数量
* y_i 为真实值
* y_hat_i 为预测值

**2.1.2 MSE的优缺点**

* **优点：**
* 对异常值敏感，能放大较大误差的影响
* 具有良好的数学性质，易于计算和优化
* **缺点：**
* 由于平方运算，MSE的值可能较大，难以直观理解
* 对异常值敏感，容易受到极端值的影响

### 2.2 平均绝对误差（MAE）

**2.2.1 MAE的定义和计算**

平均绝对误差（MAE）是预测值与真实值之间绝对差的平均值，计算公式为：

MAE = (1/n) * Σ|y_i - y_hat_i|

其中：

* n 为样本数量
* y_i 为真实值
* y_hat_i 为预测值

**2.2.2 MAE的优缺点**

* **优点：**
* 对异常值不敏感，能反映模型的整体预测精度
* 具有良好的可解释性，易于理解
* **缺点：**
* 对异常值不敏感，不能放大较大误差的影响
* 没有良好的数学性质，难以用于模型优化

### 2.3 根均方误差（RMSE）

**2.3.1 RMSE的定义和计算**

根均方误差（RMSE）是均方误差的平方根，计算公式为：

RMSE = √(MSE) = √((1/n) * Σ(y_i - y_hat_i)^2)

其中：

* n 为样本数量
* y_i 为真实值
* y_hat_i 为预测值

**2.3.2 RMSE的优缺点**

* **优点：**
* 兼具MSE和MAE的优点，既对异常值敏感，又能放大较大误差的影响
* 具有良好的可解释性，易于理解
* **缺点：**
* 由于平方根运算，RMSE的值可能较大，难以直观理解
* 对异常值敏感，容易受到极端值的影响

### 2.4 误差评估指标的选择

选择合适的误差评估指标需要考虑以下因素：

* **模型类型：**不同类型的模型对异常值和极端值有不同的敏感性。
* **数据分布：**数据分布是否对称、是否有异常值或极端值。
* **应用场景：**误差指标的解释性、可比性和对模型优化的影响。

一般来说，对于对异常值敏感的模型或数据分布不对称的情况，建议使用MAE。对于对异常值不敏感的模型或数据分布对称的情况，建议使用MSE或RMSE。

# 3.1 数据预处理和特征工程

#### 3.1.1 数据清洗和转换

数据预处理是拟合函数误差分析的关键步骤，它涉及到将原始数据转换为适合建模和分析的形式。数据清洗过程包括：

- **缺失值处理：**处理缺失值的方法包括删除缺失值、填充缺失值（如均值、中位数或众数）或使用插值技术。
- **异常值处理：**识别和处理异常值，异常值是指与数据集中的其他数据点明显不同的数据点。异常值可以删除或转换。
- **数据类型转换：**将数据转换为适当的数据类型，例如将字符串转换为数字或将日期转换为时间戳。
- **数据标准化和归一化：**对数据进行标准化或归一化，以确保不同特征具有相同的尺度。

#### 3.1.2 特征选择和降维

特征选择和降维技术用于从原始数据集中选择最相关