Python高级数据结构指南：B树、堆和优先队列详解

# 1. Python高级数据结构概述

在现代编程实践中，数据结构的合理选择和应用对于提高程序性能至关重要。Python作为一门广泛应用于数据分析、机器学习、网络开发等领域的高级语言，其内置的数据结构——列表、元组、字典和集合——为开发者提供了强大的数据处理能力。然而，在面对更为复杂和特定需求的情况下，这些基础数据结构有时无法满足性能和效率上的要求。因此，深入理解并熟练应用更高级的数据结构，如B树、堆、优先队列等，对于IT专业人员来说显得尤为重要。

本章将为读者概述Python中高级数据结构的概念和用途，为后续章节中对特定数据结构深入探讨打下基础。我们会从这些结构的特点入手，介绍它们在实际应用中的优势，以及它们如何帮助解决编程中的实际问题。通过这一章，读者应能对高级数据结构有一个初步的认识，为学习更复杂的内容做好铺垫。

# 2. B树的理论与实现

## 2.1 B树基础理论
### 2.1.1 B树的定义和特性
B树，是一种自平衡的树数据结构，它能够保持数据有序，允许搜索、顺序访问、插入和删除在对数时间内完成。B树特别适合读写相对较大的数据块的系统，例如磁盘存储或其他直接访问存储设备。

B树的关键特性包括：

- **节点大小**：B树的节点大小通常由系统页面大小决定，这使得B树特别适用于磁盘存储，每个节点的读取和写入操作对应一个磁盘页。
- **排序顺序**：B树的所有值都是按键排序的，允许有效的范围查询。
- **分支因子**：节点的分支因子（即子节点数）在最小和最大值之间变化，这取决于树的阶数（m）。一个m阶的B树，其节点至少包含[t-1]个键，其中t为树的最小度数。

### 2.1.2 B树的应用场景分析
B树的这些特性使其在多个实际应用场景中变得非常有用：

- **数据库系统**：由于B树能够高效地进行数据的插入、删除和查找操作，它被广泛用于数据库索引，尤其是那些需要处理大量数据的系统。
- **文件系统**：现代文件系统中，B树用于组织数据块的位置和管理空间，这允许文件系统高效地执行文件查找、读取和写入操作。
- **数据仓库**：数据仓库中的数据通常具有高度的层次性，B树能够高效地处理这些数据并支持复杂的查询。

## 2.2 B树的算法原理
### 2.2.1 插入操作的算法步骤
B树的插入算法确保树保持平衡，以下是插入操作的基本步骤：

1. **查找插入位置**：从根节点开始，根据键值比较向下查找直到叶子节点，找到应该插入新键值的节点位置。
2. **节点插入**：若该节点的键值数未达到最大值，则直接插入；若已满，则需进行节点分裂。
3. **分裂节点**：如果插入导致节点溢出（键值数超过最大值），则需要将节点分裂为两个节点，中间键值上移至父节点。
4. **调整树结构**：如果父节点的键值数也达到最大，继续向上分裂，直到根节点。

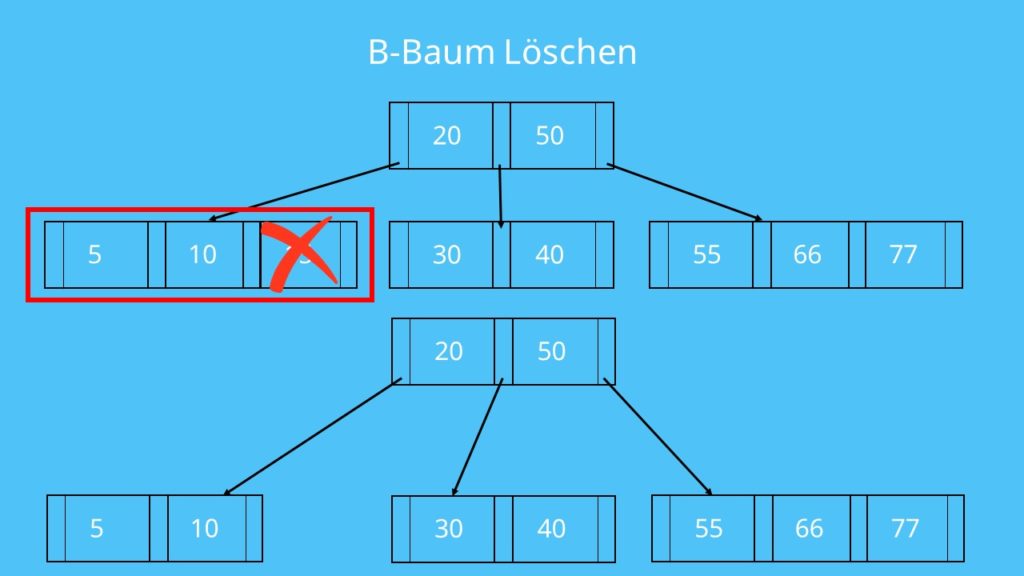
### 2.2.2 删除操作的算法步骤
B树的删除操作稍微复杂，主要步骤如下：

1. **查找删除位置**：从根节点开始，搜索要删除的键值所在的叶子节点。
2. **删除键值**：如果键值所在节点的键值数超过最小值，则直接删除；否则，需要从兄弟节点借键值或合并节点。
3. **借取和合并**：如果需要从兄弟节点借键值，将父节点的一个键值下移至当前节点，并将相应的兄弟节点中的键值上移。若无法借取，则需要与一个兄弟节点合并。
4. **调整树结构**：如果合并导致父节点的键值数减少，可能需要向上继续执行合并操作。

## 2.3 B树的Python实现
### 2.3.1 B树节点的设计
在实现B树之前，我们首先定义一个B树节点类，它包含键值列表和子节点列表：

class BTreeNode:
    def __init__(self, leaf=False):
        self.leaf = leaf  # 节点是叶子节点标志
        self.keys = []  # 存储键值的数组
        self.child = []  # 子节点列表
        self.n = 0  # 当前节点的键值数

### 2.3.2 B树的构建与操作实践
以下是一个简单的B树实现，包括插入和删除操作的示例：

class BTree:
    def __init__(self, t):
        self.root = BTreeNode(True)
        self.t = t  # 最小度数

    def insert(self, k):
        # 插入键值k的逻辑
        pass

    def delete(self, k):
        # 删除键值k的逻辑
        pass

    # 其他辅助函数，例如节点分裂、合并、调整等
    # ...

### 2.3.3 B树构建与操作代码逻辑解读
- **插入函数**：在`insert`函数中，首先调用`insert_non_full`函数将键值插入非满节点，若需要节点分裂，则递归调用自身。
- **删除函数**：`delete`函数首先找到要删除的键值所在的叶子节点，若存在，则删除；若不存在，则寻找替代节点，必要时执行节点合并操作。
- **辅助函数**：为处理节点分裂和合并等复杂情况，需编写一系列辅助函数。例如，`split_child`用于分裂子节点，`merge_child`用于合并子节点。

**注意：**在实际应用中，B树的实现可能需要考虑磁盘读写优化、持久化以及并发控制等复杂问题。上述代码为简化版本，主要用于演示算法逻辑。

# 3. 堆结构的理论与实践

## 3.1 堆的理论基础

### 3.1.1 堆的概念和性质

堆（Heap）是一种特殊的完全二叉树，通常利用数组来实现。在堆中，父节点的值总是不大于或不小于其子节点的值，这称为堆的性质。堆的这种特性使得它在实现优先队列等数据结构时非常有用，尤其是当我们需要快速获取最大或最小元素时。

堆的两种主要类型是最小堆（Min-Heap）和最大堆（Max-Heap）。在最小堆中，父节点的值小于或等于其子节点的值；而在最大堆中，父节点的值大于或等于其子节点的值。这些性质为实现高效的优先队列操作提供了基础。

堆的一个重要性质是堆的高（height）与堆中元素的个数（n）之间的关系。堆的高度可以通过对数公式 \( h = \lceil \log_2(n + 1) \rceil - 1 \) 来计算。这意味着在堆中添加或删除元素时，树的高度变化仅限于最坏情况下的对数级别。

### 3.1.2 堆与优先队列的关系

堆结构是优先队列（Priority Queue）最常用的内部实现方式。优先队列允许用户插入元素，并通过优先级规则来快速检索和删除最高优先级的元素。堆结构能够高效地支持这些操作，因为它们可以保证在 O(1) 时间内获取最大或最小元素，以及在 O(log n) 时间内完成插入和删除操作。

在堆实现的优先队列中，元素的优先级由其在堆中的位置决定，而堆的结构保证了最高优先级（最大或最小）的元素始终位于根节点。这使得在很多需要优先级排序的场景中，比如任务调度、事件驱动编程等，堆结构成为一种理想的数据结构。

## 3.2 堆的操作算法

### 3.2.1 堆的调整算法

堆调整算法是维持堆性质的关键，对于一个已经部分构建的堆，调整算法可以帮助我们在添加或删除元素后恢复其堆性质。堆的调整通常有两种形式：上滤（Percolate Up）和下滤（Percolate Down）。

上滤算法用于插入操作，当一个新元素被添加到堆中时，它首先被放置到堆的底部（数组的末尾）。之后，算法比较这个新元素与其父节点的值，如果新元素的值比父节点的值小（对于最小堆）或大（对于最大堆），则它们交换位置，这个过程一直持续到新元素到达堆的顶部或者不再需要交换为止。

下滤算法用于删除操作，当需要删除堆中的最小（或最大）元素时，它通常被替换为堆的最后一个元素，然后被“沉”到合适的位置。在下滤过程中，新位于根位置的元素与其子节点比较，如果需要，与较小（或较大）的子节点交换位置，继续下滤直到该元素的子树满足堆性质为止。

### 3.2.2 堆的插入与删除操作

堆的插入和删除操作是通过上述的堆调整算法实现的。插入操作通过上滤实现，而删除操作则通过下滤实现。这两者都是堆数据结构实现优先队列的基础。

插入操作：向堆中添加一个新元素，首先将其放在数组的末尾，然后执行上滤操作，以维护堆的性质。

删除操作：从堆中删除并返回最小（或最大）元素。这通常意味着移除根节点并将最后一个元素放到根的位置，接着执行下滤操作。

这些操作的时间复杂度在最坏情况下均为 O(log n)，其中 n 是堆中元素的数量。堆的这种高效性能特别适合处理需要频繁添加或删除操作的场景。

## 3.3 堆的Python实现

### 3.3.1 最小堆和最大堆的实现

Python 中没有内置的堆结构，但可以利用 `heapq` 模块提供的接口来实现最小堆