Python栈与队列解析：掌握数据流动的艺术

# 1. Python中栈与队列的概念和应用

在编程和数据结构的世界中，栈（Stack）和队列（Queue）是两种基本而重要的数据结构。本章将介绍栈与队列的基本概念，并探索它们在Python编程中的应用。

## 1.1 栈与队列的基础
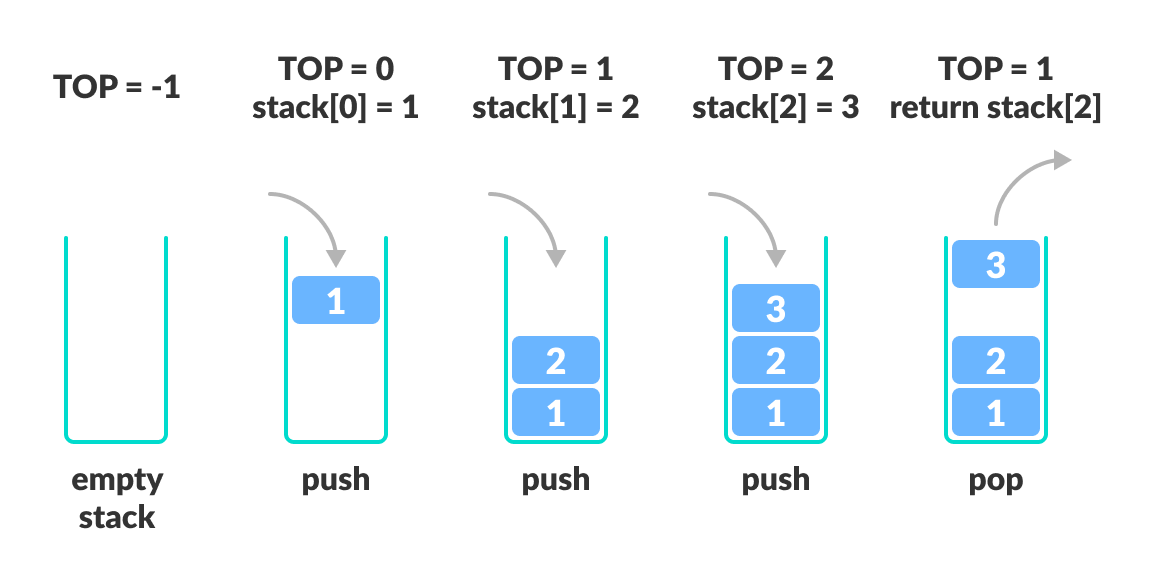
栈是一种后进先出（LIFO）的数据结构，它允许操作的集合只限于顶部元素，从而支持两种主要操作：推送（push）和弹出（pop）。而队列是一种先进先出（FIFO）的数据结构，支持在队列尾部添加元素（入队），以及在队列头部移除元素（出队）。这两种数据结构在各种编程问题中扮演着关键角色，尤其是在处理需要特定顺序操作的场景。

## 1.2 栈与队列的应用场景
栈与队列的应用广泛且多样。栈常用于解决需要逆序处理数据的问题，例如表达式求值、括号匹配以及回溯算法。队列则在任务调度、事件处理等需要按顺序执行的场景中非常有用，广度优先搜索和缓存策略是队列应用的典型例子。

## 1.3 栈与队列的Python实现概述
在Python中，可以通过内置的数据类型如列表（list）来实现栈与队列。列表提供了添加和移除元素的方法，能够便捷地模拟栈和队列的行为。此外，Python标准库中的`collections.deque`可以用来创建高效的队列实现。

本章为理解后续章节中栈与队列的具体实现和应用打下了基础，接下来的章节将逐步深入探讨栈与队列在Python中的实现细节和应用实例。

# 2. 栈在Python中的实现和应用

栈是一种遵循后进先出（LIFO, Last In First Out）原则的抽象数据类型，允许我们执行两种操作：压栈（push）将元素添加到栈顶，弹栈（pop）从栈顶移除元素。Python中并没有内置的栈实现，但我们可以通过列表（list）这一内置的数据结构来模拟栈的行为。这一章节，我们将深入探索栈的理论基础，并通过Python实践案例来展示栈的多功能性。

### 2.1 栈的基本理论和数据结构

#### 2.1.1 栈的定义和特性

栈是一个集合，其中的数据元素遵循后进先出（LIFO）的原则。在栈中，最后一个被添加到集合中的元素将是第一个被移除的。这种特性让栈非常适合解决逆序相关的问题，例如，当我们需要反向遍历一个序列时，可以使用栈来存储元素并在后续进行反向弹出。

#### 2.1.2 栈的操作和实现方法

在Python中，我们可以使用列表的append()和pop()方法来模拟栈的行为。append()方法可以将元素添加到列表的末尾，等同于栈中的压栈操作。pop()方法默认移除列表的最后一个元素，对应于栈的弹栈操作。此外，我们还可以使用列表的index()方法和insert()方法来实现非标准的栈操作，例如查找并删除栈顶元素。

class Stack:
    def __init__(self):
        self.items = []

    def is_empty(self):
        return len(self.items) == 0

    def push(self, item):
        self.items.append(item)

    def pop(self):
        if not self.is_empty():
            return self.items.pop()
        return None

    def peek(self):
        if not self.is_empty():
            return self.items[-1]
        return None

    def size(self):
        return len(self.items)

上面的代码定义了一个简单的栈类，我们可以通过其方法来操作栈：

- `is_empty()` 检查栈是否为空。
- `push(item)` 将元素压入栈顶。
- `pop()` 弹出栈顶元素。
- `peek()` 查看栈顶元素而不移除它。
- `size()` 返回栈的大小。

### 2.2 栈在算法中的应用

#### 2.2.1 栈的递归算法应用

递归算法通常通过将问题分解为更小的子问题来解决，然后将这些子问题的解合并起来得到最终的答案。在递归过程中，函数调用自身，它将创建一个函数调用栈。栈中每一项都是一个函数调用的上下文，包括局部变量和返回地址等信息。

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n-1)

在上面的阶乘函数中，每次递归调用都创建了一个新的栈帧，存储了局部变量和返回地址。

#### 2.2.2 栈在表达式求值中的应用

栈的一个典型应用是表达式求值。例如，使用栈来计算后缀表达式（逆波兰表示法）的值：

def evaluate_postfix(expression):
    stack = []
    for token in expression.split():
        if token.isdigit():
            stack.append(int(token))
        else:
            right = stack.pop()
            left = stack.pop()
            if token == '+':
                stack.append(left + right)
            elif token == '-':
                stack.append(left - right)
            elif token == '*':
                stack.append(left * right)
            elif token == '/':
                stack.append(left / right)
    return stack.pop()

#### 2.2.3 栈在括号匹配问题中的应用

括号匹配是栈的另一个常见应用。通过使用栈，我们可以快速检查字符串中的括号是否正确匹配：

def is_parentheses_balanced(expression):
    stack = []
    open_parens = "([{"
    match = dict(zip(")]}", "([{"))
    for char in expression:
        if char in open_parens:
            stack.append(char)
        elif char in ")]}":
            if stack == [] or match[char] != stack.pop():
                return False
    return stack == []

### 2.3 栈的Python实践案例

#### 2.3.1 使用栈实现浏览器的后退功能

浏览器的后退功能可以使用栈来实现，因为后退操作就是返回到上一个访问过的页面。每次点击一个新的链接时，将当前页面压入栈中。点击后退按钮时，弹出栈顶元素，也就是上一个访问的页面。

class BrowserHistory:
    def __init__(self):
        self.history = []

    def visit(self, url):
        self.history.append(url)

    def back(self):
        if len(self.history) > 1:
            self.history.pop()  # 返回上一个URL，但不删除它
        return self.history[-1] if self.history else None

#### 2.3.2 使用栈解决汉诺塔问题

汉诺塔问题是一个经典的递归问题，可以使用栈来模拟递归过程。问题的目标是将一系列不同大小的盘子从一个塔移动到另一个塔，每次只能移动一个盘子，并且在移动过程中大盘子不能放在小盘子上面。

def hanoi(n, source, target, auxiliary):
    if n > 0:
        # 将 n-1 个盘子从源塔移动到辅助塔
        ha