MATLAB神经网络算法：预测模型的终极武器

# 1. MATLAB神经网络算法概述**

MATLAB神经网络算法是利用MATLAB平台实现的神经网络算法。神经网络是一种受人脑启发的机器学习模型，它能够从数据中学习复杂的关系并做出预测。

MATLAB神经网络算法具有以下特点：

* **易用性：**MATLAB提供了直观的工具箱和函数，使神经网络的创建、训练和评估变得容易。
* **强大的功能：**MATLAB神经网络工具箱支持各种神经网络架构，包括前馈网络、递归网络和卷积神经网络。
* **可扩展性：**MATLAB神经网络算法可以扩展到大型数据集和复杂问题，使其适用于广泛的应用。

# 2.1 人工神经元的模型

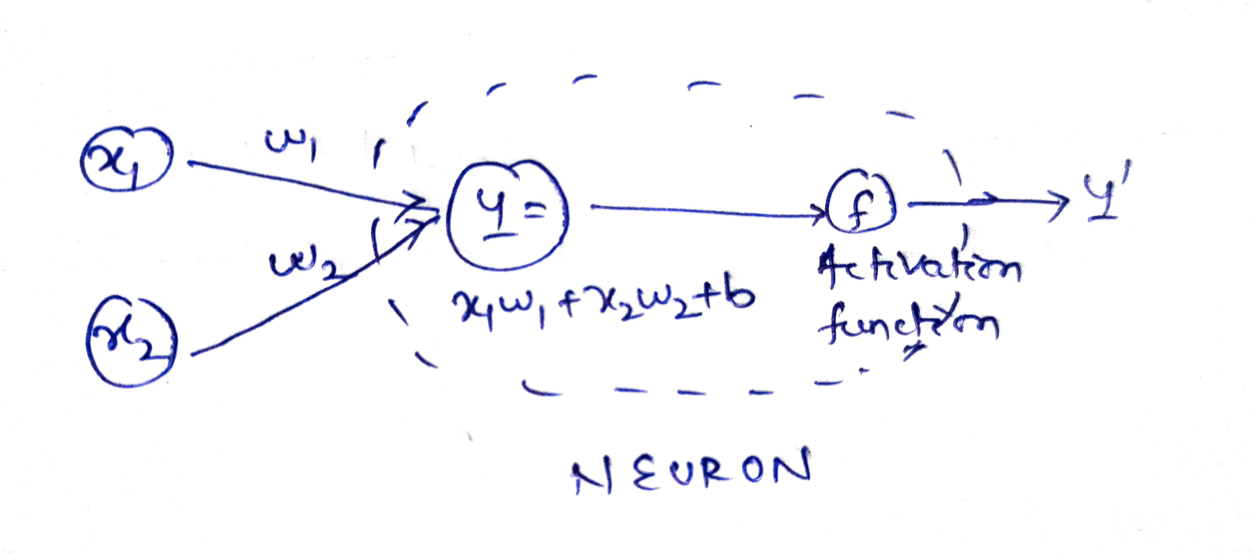
人工神经元是神经网络的基本单元，它模拟了生物神经元的功能。它接收输入信号，将其处理并产生输出信号。人工神经元的模型通常由以下几个部分组成：

**1. 输入层**

输入层接收来自外部环境或其他神经元的输入信号。这些信号可以是连续值或离散值，并且可以有多个输入。

**2. 权重**

每个输入信号都与一个权重相关联。权重决定了该输入信号对神经元输出的影响。权重可以是正值或负值，正值表示输入信号对输出有正向影响，负值表示输入信号对输出有负向影响。

**3. 偏置**

偏置是一个常数，它被添加到输入信号的加权和中。偏置允许神经元在没有输入信号的情况下产生输出。

**4. 激活函数**

激活函数是非线性函数，它将输入信号的加权和转换为输出信号。激活函数有多种类型，最常见的激活函数包括 sigmoid 函数、tanh 函数和 ReLU 函数。

**5. 输出层**

输出层产生神经元的最终输出信号。输出信号可以是连续值或离散值，并且可以有多个输出。

**人工神经元的数学模型**

人工神经元的数学模型可以表示为：

y = f(w1 * x1 + w2 * x2 + ... + wn * xn + b)

其中：

* y 是神经元的输出信号
* x1, x2, ..., xn 是输入信号
* w1, w2, ..., wn 是权重
* b 是偏置
* f 是激活函数

**代码块：**

import numpy as np

# 定义输入信号
x = np.array([1, 2, 3])

# 定义权重
w = np.array([0.5, 0.3, 0.2])

# 定义偏置
b = 0.1

# 计算加权和
z = np.dot(x, w) + b

# 定义激活函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# 计算输出信号
y = sigmoid(z)

print(y)  # 输出：0.8807970779778823

**逻辑分析：**

这段代码演示了人工神经元的数学模型。它首先定义了输入信号、权重和偏置。然后，它计算加权和并使用 sigmoid 函数作为激活函数。最后，它打印输出信号。

**参数说明：**

* `x`：输入信号，是一个 numpy 数组。
* `w`：权重，是一个 numpy 数组。
* `b`：偏置，是一个浮点数。
* `z`：加权和，是一个浮点数。
* `sigmoid`：sigmoid 激活函数，是一个 Python 函数。
* `y`：输出信号，是一个浮点数。

# 3. MATLAB神经网络工具箱

### 3.1 神经网络工具箱的简介

MATLAB神经网络工具箱是一个功能强大的环境，用于设计、训练和部署神经网络。它提供了一系列函数和工具，可以简化神经网络开发过程，并使研究人员和从业者能够快速有效地构建和评估神经网络模型。

### 3.2 神经网络的创建和训练

**神经网络的创建**

MATLAB神经网络工具箱提供了多种创建神经网络的方法。最简单的方法是使用`newff`函数，该函数根据指定的神经网络类型、层数和节点数创建前馈神经网络。对于更复杂的神经网络，可以使用`newrb`、`newpnn`和`newgrnn`等函数创建径向基、概率神经网络和广义回归神经网络。

% 创建一个具有3层（输入层、隐藏层、输出层）的前馈神经网络，其中隐藏层有10个节点
net = newff([0 1; 0 1], [10 1], {'logsig', 'purelin'});

**神经网络的训练**

神经网络的训练过程涉及调整网络权重和偏差，以最小化训练数据集上的误差。MATLAB神经网络工具箱提供了多种训练算法，包括反向传播、Levenberg-Marquardt和共轭梯度法。

% 使用反向传播算法训练神经网络
net = train(net, inputs, targets);

### 3.3 神经网络的评估和优化

**神经网络的评估**

训练后，需要评估神经网络的性能。MATLAB神经网络工具箱提供了多种评估指标，包括均方误差、分类准确率和回归相关系数。

% 计算神经网络在测试数据集上的均方误差
mse = mean((net(inputs_test) - targets_test).^2);

**神经网络的优化**

为了提高神经网络的性能，可以进行优化。MATLAB神经网络工具箱提供了多种优化技术，包括正则化、早期停止和权重衰减。

% 使用正则化优化神经网络
net = train(net, inputs, targets, 'useRegulazation', 'on');

**表格：MATLAB神经网络工具箱中的常用函数**

| 函数 | 用途 |
|---|---|
| `newff` | 创建前馈神经网络 |
| `newrb` | 创建径向基神经网络 |
| `newpnn` | 创建概率神经网络 |
| `newgrnn` | 创建广义回归神经网络 |
| `train` | 训练神经网络 |
| `mse` | 计算均方误差 |
| `trainlm` | 使用Levenberg-Marquardt算法训练神经网络 |
| `traingd` | 使用共轭梯度法训练神经网络 |

**流程图：MATLAB神经网络工具箱中神经网络开发流程**

[流程图]

mermaid
graph LR
subgraph 创建神经网络
    A[创建前馈神经网络] --> B[创建径向基神经网络]
    B --> C[创建概率神经网络]
    C --> D[创建广义回归神经网络]
end
subgraph 训练神经网络
    D --> E[使用反向传播算法]
    D --> F[使用Levenberg-Marquardt算法]
    D --> G[使用共轭梯度法]
end
subgraph 评估和优化神经网络
    E --> H[计算均方误差]
    F --> H
    G --> H
    H --> I[使用正则化]
    H --> J[使用早期停止]
    H --> K[使用权重衰减]
end

# 4. MATLAB神经网络算法实践**

**4.1 回归问题的神经网络模型**

**4.1.1 数据预处理和模型构建**

回归问题的神经网络模型旨在预测连续值的目标变量。在构建模型之前，需要对数据进行预处理，包括：

- **数据归一化：**将数据缩放到 [0, 1] 范围，以提高训练效率。
- **特征缩放：**将特征缩放至均值为 0、标准差为 1，以减少特征之间的差异。

数据预处理完成后，可以使用 `fitnet` 函数创建神经网络模型。该函数接受以下参数：

net = fitnet(hiddenLayerSize, trainFcn, perfFcn)

其中：

- `hiddenLayerSize`：隐藏层的神经元数量。
- `trainFcn`：训练算法，例如 `trainlm`（Levenberg-Marquardt 算法）。
- `perfFcn`：性能函数，例如 `mse`（均方误差）。

**4.1.2 模型训练和评估**

模型创建后，可以使用 `train` 函数进行训练。该函数接受以下参数：

net = train(net, inputs, targets)

其中：

- `net`：神经网络模型。
- `inputs`：训练数据输入。
- `targets`：训练数据目标。

训练完成后，可以使用 `mse` 函数评估模型的性能。该函数计算均方误差，即预测值与实际值之间的平均平方差。

**4.2 分类问题的神经网络模型**

**4.2.1 数据预处理和模型构建**

分类问题的神经网络模型旨在预测离散值的目标变量。数据预处理包括：

- **独热编码：**将类别变量转换为二进制向量。
- **特征缩放：**与回归问题类似。

可以使用 `patternnet` 函数创建分类神经网络模型。该函数接受以下参数：

net = patternnet(hiddenLayerSize, trainFcn, perfFcn)

参数与回归问题中的 `fitnet` 函数类似。

**4.2.2 模型训练和评估**

模型创建后，可以使用 `train` 函数进行训练。该函数接受以下参数：

net = train(net, inputs, targets)

其中：

- `net`：神经网络模型。
- `inputs`：训练数据输入。
- `targets`：训练数据目标（独热编码）。

训练完成后，可以使用 `classificationAccuracy` 函数评估模型的性能。该函数计算分类准确率，即正确预测的样本数量与总样本数量之比。

# 5. 神经网络算法的应用

神经网络算法在各种领域都有广泛的应用，包括金融预测、医疗诊断和图像识别。

### 5.1 金融预测

神经网络算法可以用于预测金融市场中的趋势和模式。通过分析历史数据，神经网络可以学习识别影响金融市场表现的复杂关系。这使它们能够预测股票价格、汇率和商品价格等金融指标的未来值。

### 5.2 医疗诊断

神经网络算法在医疗诊断中发挥着越来越重要的作用。它们可以分析患者的医疗记录、实验室结果和影像数据，以识别疾病和预测疾病进展。这有助于医生做出更准确的诊断，并制定更有效的治疗计划。

### 5.3 图像识别

神经网络算法在图像识别领域取得了显著的成功。它们可以识别图像中的物体、面部和场景。这使它们适用于各种应用，例如面部识别、图像分类和自动驾驶。

**代码示例：使用 MATLAB 神经网络工具箱进行图像识别**

% 加载图像数据
data = load('image_data.mat');

% 创建神经网络
net = feedforwardnet([100, 50]);

% 训练神经网络
net = train(net, data.input, data.output);

% 评估神经网络
performance = net(data.input, data.output);

% 显示结果
figure;
plot(performance);
title('神经网络图像识别性能');

**逻辑分析：**

* `load` 函数加载图像数据。
* `feedforwardnet` 函数创建一个前馈神经网络，具有 100 个隐藏层神经元和 50 个输出层神经元。
* `train` 函数使用反向传播算法训练神经网络。
* `net` 函数使用训练后的神经网络对新数据进行预测。
* `performance` 函数计算神经网络的性能，例如准确率和损失函数。
* `plot` 函数绘制神经网络的性能图。

# 6.1 深度学习的兴起

随着计算能力的不断提升和海量数据的涌现，深度学习近年来取得了长足的发展。深度学习是一种神经网络算法，它具有多层隐藏层，可以学习复杂的数据模式和特征。

深度学习模型通常由卷积层、池化层、全连接层等模块组成。卷积层可以提取数据的局部特征，池化层可以降低数据的维度，全连接层可以将提取的特征映射到最终的输出。

深度学习算法在图像识别、自然语言处理、语音识别等领域取得了突破性的进展。例如，谷歌的 AlphaGo 围棋程序就是基于深度学习算法构建的，它能够击败世界顶尖的围棋选手。

### 6.1.1 深度学习模型的优势

深度学习模型具有以下优势：

- **强大的特征学习能力：**深度学习模型可以从数据中自动学习特征，而无需人工干预。
- **高精度：**深度学习模型在许多任务上可以达到甚至超过人类专家的精度。
- **泛化能力强：**深度学习模型可以很好地泛化到新的数据，即使这些数据与训练数据不同。

### 6.1.2 深度学习模型的挑战

深度学习模型也面临着一些挑战：

- **计算量大：**深度学习模型的训练需要大量的计算资源。
- **数据需求量大：**深度学习模型需要大量的数据才能训练出良好的性能。
- **易过拟合：**深度学习模型容易过拟合训练数据，导致在测试数据上的性能较差。