马尔科夫链在图算法中的应用与求解方法

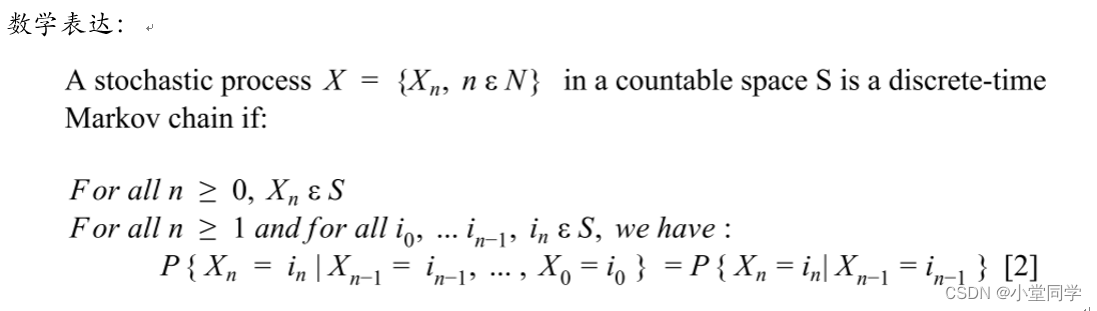
# 1. 马尔科夫链的基本原理和性质

马尔科夫链是一种随机过程，其中每个状态的未来演变仅取决于其当前状态，与过去的状态无关。这一性质称为马尔科夫性质。

马尔科夫链可以用一个转移矩阵来表示，该矩阵包含从一个状态转移到另一个状态的概率。转移矩阵的元素满足以下性质：

- 行和为 1：每一行之和都为 1，表示从一个状态转移到所有其他状态的概率总和为 1。
- 非负性：转移矩阵中的所有元素都为非负，表示从一个状态转移到另一个状态的概率不能为负。

# 2. 马尔科夫链在图算法中的应用

马尔科夫链是一种随机过程，它描述了一个系统在不同状态之间转移的概率。在图算法中，马尔科夫链可以用来解决各种问题，包括随机游走、图聚类和图生成。

### 2.1 马尔科夫链在随机游走中的应用

#### 2.1.1 随机游走的定义和性质

随机游走是一种在图中随机移动的算法。在每次移动中，算法从当前节点随机选择一个相邻节点并移动到该节点。随机游走的性质包括：

- **马尔可夫性：**随机游走是马尔科夫链，因为下一个节点的选择仅取决于当前节点，与之前访问的节点无关。
- **遍历性：**如果图是连通的，随机游走最终将遍历所有节点。
- **平稳性：**在长期运行后，随机游走将达到稳态分布，其中每个节点被访问的概率与该节点的度数成正比。

#### 2.1.2 马尔科夫链在随机游走中的建模

我们可以使用马尔科夫链来对随机游走建模。马尔科夫链的状态是图中的节点，转移概率是节点之间转移的概率。

import numpy as np

# 创建转移概率矩阵
P = np.array([[0.2, 0.3, 0.5],
              [0.4, 0.2, 0.4],
              [0.3, 0.5, 0.2]])

# 初始化状态分布
state = np.array([1, 0, 0])

# 运行随机游走
for i in range(100):
    # 根据当前状态选择下一个状态
    next_state = np.random.choice(3, p=P[state])
    # 更新状态
    state = next_state

在上面的代码中，转移概率矩阵 `P` 表示从一个节点转移到另一个节点的概率。状态 `state` 表示当前节点。每次迭代，我们根据当前状态从转移概率矩阵中选择下一个状态，并更新 `state`。

### 2.2 马尔科夫链在图聚类中的应用

#### 2.2.1 图聚类的概念和方法

图聚类是一种将图中的节点划分为组或簇的过程。图聚类的方法包括：

- **基于连通性的聚类：**将连通的节点聚类在一起。
- **基于相似性的聚类：**将相似节点聚类在一起。
- **基于马尔科夫链的聚类：**使用马尔科夫链来确定节点之间的相似性并进行聚类。

#### 2.2.2 马尔科夫链在图聚类中的算法

基于马尔科夫链的图聚类算法包括：

- **谱聚类：**使用马尔科夫链的转移概率矩阵来构造图的拉普拉斯矩阵，然后对拉普拉斯矩阵进行谱分解。
- **随机游走聚类：**使用随机游走来确定节点之间的相似性，然后使用聚类算法（如 k-means）将节点聚类在一起。

### 2.3 马尔科夫链在图生成中的应用

#### 2.3.1 图生成的模型和方法

图生成是一种创建具有特定属性的图的过程。图生成的方法包括：

- **随机图生成：**生成具有随机连接的图。
- **基于马尔科夫链的图生成：**使用马尔科夫链来生成具有特定拓扑结构的图。
- **基于深度学习的图生成：**使用深度学习模型来生成具有复杂结构的图。

#### 2.3.2 马尔科夫链在图生成中的算法

基于马尔科夫链的图生成算法包括：

- **随机游走图生成：**使用随机游走来生成具有特定度分布的图。
- **马尔科夫链蒙特卡罗图生成：**使用马尔科夫链蒙特卡罗方法来生