拓扑维护问题：解决动态图变化下的拓扑排序

# 1. 拓扑排序基础**

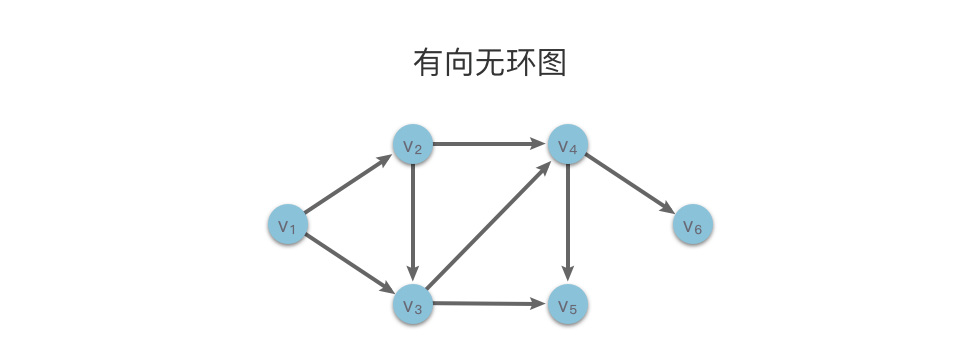
拓扑排序是一种算法，用于对有向无环图（DAG）中的顶点进行排序，使得对于图中任意两条边 (u, v)，如果 u 在排序中排在 v 之前，则 v 不会指向 u。拓扑排序在软件包依赖管理、任务调度和数据分析等领域有着广泛的应用。

# 2. 动态图拓扑排序算法

### 2.1 Kahn算法

#### 2.1.1 算法原理

Kahn算法是一种拓扑排序算法，适用于有向无环图（DAG）。算法的基本思想是：

1. 初始化一个空队列，用于存储拓扑排序后的结果。
2. 对于图中的每个顶点，计算其入度（即指向该顶点的边的数量）。
3. 将入度为0的顶点加入队列。
4. 循环执行以下步骤，直到队列为空：
- 从队列中取出一个顶点。
- 将该顶点加入拓扑排序结果中。
- 对于该顶点指向的所有顶点，将它们的入度减1。
- 如果某个顶点的入度变为0，将其加入队列。

#### 2.1.2 算法步骤

def kahn_topological_sort(graph):
    """
    Kahn算法进行拓扑排序

    :param graph: 有向无环图，用邻接表表示
    :return: 拓扑排序结果
    """
    # 初始化入度表
    in_degrees = [0] * len(graph)
    for node in graph:
        for neighbor in graph[node]:
            in_degrees[neighbor] += 1

    # 初始化队列
    queue = []
    for node in graph:
        if in_degrees[node] == 0:
            queue.append(node)

    # 拓扑排序结果
    result = []

    # 循环处理队列
    while queue:
        # 取出队列中的第一个顶点
        node = queue.pop(0)

        # 将该顶点加入拓扑排序结果
        result.append(node)

        # 更新入度表
        for neighbor in graph[node]:
            in_degrees[neighbor] -= 1
            if in_degrees[neighbor] == 0:
                queue.append(neighbor)

    return result

**代码逻辑逐行解读：**

1. `in_degrees = [0] * len(graph)`：初始化入度表，长度为图中顶点的数量，每个元素初始化为0。
2. `for node in graph:`：遍历图中的每个顶点。
3. `for neighbor in graph[node]:`：遍历该顶点指向的所有顶点。
4. `in_degrees[neighbor] += 1`：更新指向顶点的入度。
5. `queue = []`：初始化队列。
6. `for node in graph:`：遍历图中的每个顶点。
7. `if in_degrees[node] == 0:`：如果顶点的入度为0，则将其加入队列。
8. `result = []`：初始化拓扑排序结果。
9. `while queue:`：循环处理队列，直到队列为空。
10. `node = queue.pop(0)`：取出队列中的第一个顶点。
11. `result.append(node)`：将该顶点加入拓扑排序结果。
12. `for neighbor in graph[node]:`：遍历该顶点指向的所有顶点。
13. `in_degrees[neighbor] -= 1`：更新指向顶点的入度。
14. `if in_degrees[neighbor] == 0:`：如果指向顶点的入度为0，则将其加入队列。
15. `return result`：返回拓扑排序结果。

### 2.2 DFS算法

#### 2.2.1 算法原理

DFS算法（深度优先搜索）也可以用于进行拓扑排序。算法的基本思想是：

1. 从图中的任意一个顶点开始进行DFS。
2. 在DFS过程中，将访问过的顶点标记为已访问。
3. 当访问一个顶点时，如果其所有指向的顶点都已访问，则将该顶点加入拓扑排序结果中。

#### 2.2.2 算法步骤

def dfs_topolo