主题模型深度解析：LDA算法优化与应用实战

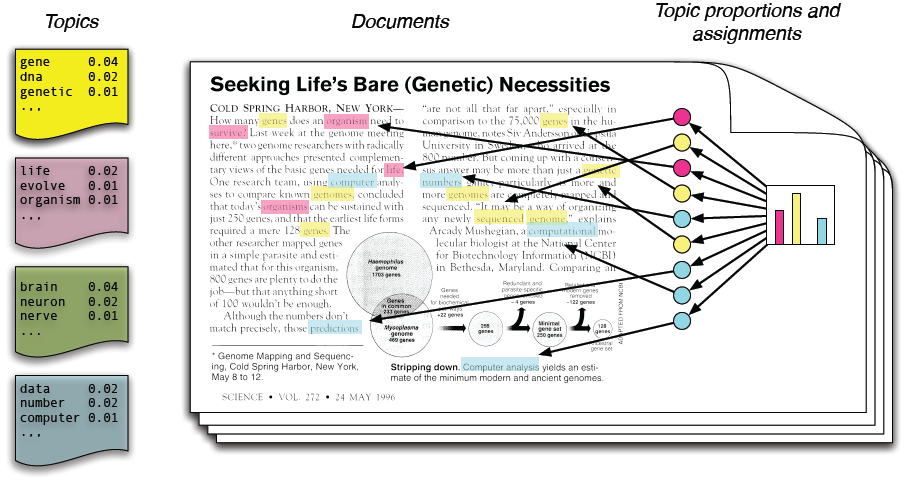
# 1. 主题模型与LDA算法概述

主题模型是自然语言处理和文本挖掘领域中用于发现大量文档集合中隐含主题的技术。LDA（Latent Dirichlet Allocation，潜在狄利克雷分配）算法是其中最具代表性的无监督学习模型之一，它通过统计手段将文档集合中的词义关联起来，形成可以解释的“主题”。LDA模型不仅能揭示文档的隐含结构，还能用于文本分类、信息检索、推荐系统等众多应用领域。通过利用LDA，我们可以更有效地组织、探索和理解大规模文档数据集。在本章中，我们将探讨LDA算法的基本原理和其在现实世界应用的概览。

# 2. LDA算法的数学原理与实现

### 2.1 LDA算法的理论基础

#### 2.1.1 概率主题模型的概念

概率主题模型是一种用于发现文档集合中隐藏的“主题”的统计模型。每个主题被定义为一个潜在的、可以产生一系列词的概率分布。文档被视为主题的混合，而每个主题则通过一系列词的概率分布来表示。这样的模型使我们能够用概率的视角来分析文本数据，并识别出文档中潜在的主题结构。

#### 2.1.2 LDA模型的贝叶斯推断框架

LDA（Latent Dirichlet Allocation）是一种典型的概率主题模型，由Blei、Ng和Jordan于2003年提出。在LDA模型中，每个文档被看作是主题的一个概率分布，而每个主题则是词的一个概率分布。该模型的参数通常通过贝叶斯推断来估计，需要对文档集进行多次迭代，逐步逼近文档和词汇的潜在主题分布。

### 2.2 LDA算法的统计推断过程

#### 2.2.1 Gibbs采样技术

Gibbs采样是一种基于马尔可夫链蒙特卡洛（MCMC）方法的统计推断技术，用于解决多变量概率分布的估计问题。在LDA中，Gibbs采样通过迭代地重新分配每个词的主题标签，直到达到收敛状态。每次迭代中，给定其他词的主题分配，一个词的主题标签是从条件分布中随机选择的。Gibbs采样在文档主题分布和词汇主题分布的估计中非常有效。

import numpy as np
from sklearn.datasets import make_multilabel_classification
from scipy.special import digamma, gammaln
from numpy.random import choice, gamma

def gibbs_sampling_step(topic_word_counts, doc_topic_counts, vocab_size, num_topics, alpha, beta):
    """
    One iteration of Gibbs sampling for LDA model.
    """
    for doc_index in range(len(doc_topic_counts)):
        for word_index in range(len(doc_topic_counts[doc_index])):
            # Remove the current topic for the word
            current_topic = doc_topic_counts[doc_index][word_index]
            topic_word_counts[current_topic][doc_topic_counts[doc_index][word_index]] -= 1
            # Calculate probabilities for all topics
            probabilities = []
            for topic in range(num_topics):
                p = (doc_topic_counts[doc_index][topic] + alpha) * \
                    (topic_word_counts[topic][doc_topic_counts[doc_index][word_index]] + beta) / \
                    (topic_word_counts[topic] + beta * vocab_size)
                probabilities.append(p)
            probabilities = probabilities / np.sum(probabilities)

            # Choose new topic based on probabilities
            new_topic = np.random.multinomial(1, probabilities).argmax()
            doc_topic_counts[doc_index][word_index] = new_topic
            # Add the new topic for the word
            topic_word_counts[new_topic][doc_topic_counts[doc_index][word_index]] += 1

#### 2.2.2 变分贝叶斯方法

变分贝叶斯（Variational Bayes）方法是另一种在LDA模型中常用的推断技术。它通过寻找一个简单的分布来近似复杂的后验分布，这个过程称为变分推断。变分推断通常涉及最大化一个证据下界（ELBO），这是一个衡量模型拟合度和复杂度的指标。变分方法相比Gibbs采样而言，计算更为高效，并能更好地控制模型复杂度。

### 2.3 LDA算法的Python实现

#### 2.3.1 使用gensim库实现LDA

Python中实现LDA算法的库有很多，其中gensim库因其简洁和效率而受到青睐。以下是使用gensim实现LDA的基本代码示例：

from gensim import corpora, models

# 构建词典和语料库
dictionary = corpora.Dictionary(document_list)
corpus = [dictionary.doc2bow(doc) for doc in document_list]

# 使用gensim训练LDA模型
lda_model = models.LdaModel(corpus, num_topics=10, id2word=dictionary, passes=15)

# 打印主题
topics = lda_model.print_topics(num_words=4)
for topic in topics:
    print(topic)

#### 2.3.2 代码解读与参数调优

在使用gensim实现LDA时，需要对多个参数进行调整以优化模型性能。例如，`num_topics`参数用于指定模型中主题的数量；`passes`参数表示训练数据通过算法的次数，它影响模型训练的时间和结果质量。此外，`alpha`和`beta`参数分别控制文档-主题分布和主题-词分布的平滑程度。合适的参数选择需要结合具体的数据集和问题进行调整。通过多次实验和使用诸如困惑度（perplexity）这样的评估指标来指导参数的选择。

以上内容仅仅是对LDA算法数学原理与实现的初步介绍，我们会在后续章节中进行深入的探讨和实战演练。

# 3. LDA算法的优化策略

## 3.1 算法效率的优化

### 3.1.1 并行计算与分布式处理

LDA算法在处理大规模数据集时，计算量是巨大的。传统的单机处理方式，在时间和资源上都可能显得力不从心。因此，采用并行计算和分布式处理成为了优化LDA算法效率的重要手段。

并行计算通过在多核或多节点上同时执行计算任务，能够显著提高算法处理速度。在LDA算法中，可以通过将文档集合分割成多个子集，并行地在这些子集上进行模型训练和参数更新。在Python中，可以使用多进程（multiprocessing）或者并行计算库如Dask、Spark等实现这一点。

分布式处理通常意味着在不同的机器上执行计算任务，这些机器之间通过网络进行通信。像Apache Spark这样的分布式计算框架提供了高级API，可以简化大规模数据处理。LDA算法的参数更新可以映射为map-reduce操作，即在所有节点上独立计算局部参数（map），然后汇总这些参数以更新全局模型（reduce）。

在具体实施时，需要注意数据的局部性原理以减少网络传输开销，并且要合理设计算法以避免频繁的全局同步，这在分布式系统中可能是性能瓶颈。

### 3.1.2 优化算法收敛速度

LDA算法的收敛速度直接影响模型训练的效率，加快收敛速度可以缩短模型训练的时间。一种常用的方法是初始化方法的改进，通过合理的初始参数设置可以避免算法收敛到局部最优解。

另外，采用更高效的参数更新策略也是一个常见的优化手段。例如，通过增加更频繁的参数更新或者采用在线学习方法，可以使得模型更快地适应数据变化，从而提高收敛速度。

在代码实现上，可以引入自适应的学习率调整机制，如AdaGrad或Adam优化算法，它们可以根据历史梯度信息调整每个参数的学习率，从而加速收敛。

# 示例代码：使用Adam优化器的参数更新
from keras.optimizers import Adam

# 定义Adam优化器，设置合适的初始学习率
adam = Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0)

# 在模型训练时应用优化器
***pile(optimizer=adam, loss='categorical_crossentropy', metrics=['accuracy'])

在上述代码中，`Adam`优化器被应用于模型的编译阶段，通过调整学习率（`lr`）、一阶矩估计系数（`beta_1`）和二阶矩估计系数（`beta_2`）等参数来优化学习过程。

## 3.2 算法性能的提升

### 3.2.1 模型过拟合的处理

LDA作为一种生成模型，和许多机器学习算法一样，容易遇到过拟合的问题，尤其是当主题数目设置过多或者文档数量较少时。处理过拟合的主要方法包括但不限于增加训练数据量、引入正则化技术以及对模型结构进行简化。

增加数据量是最直接的方法，它能够提供更丰富的信息以防止模型过度依赖于训练集中的噪声。

正则化技术在LDA中的应用主要是通过向模型引入惩罚项（如L1或L2正则项）来限制模型复杂度，防止模型过度拟合。

模型简化意味着减少模型中的自由度，比如通过合并一些稀疏的主题，减少主题数目，或者限制模型的超参数。

# 示例代码：在使用gensim库实现LDA时添加正则化项
from gensim.models.ldamodel import LdaModel

# 训练带有正则化的LDA模型
lda_model = LdaModel(corpus=corpus, id2word=id2word, num_topics=10,
                     alpha='auto', eta='auto', minimum_probability=0.01,
                     minimum_phi_value=0.01, per_word_topics=F