MATLAB对角矩阵的运算：加、减、乘、除的深入探讨

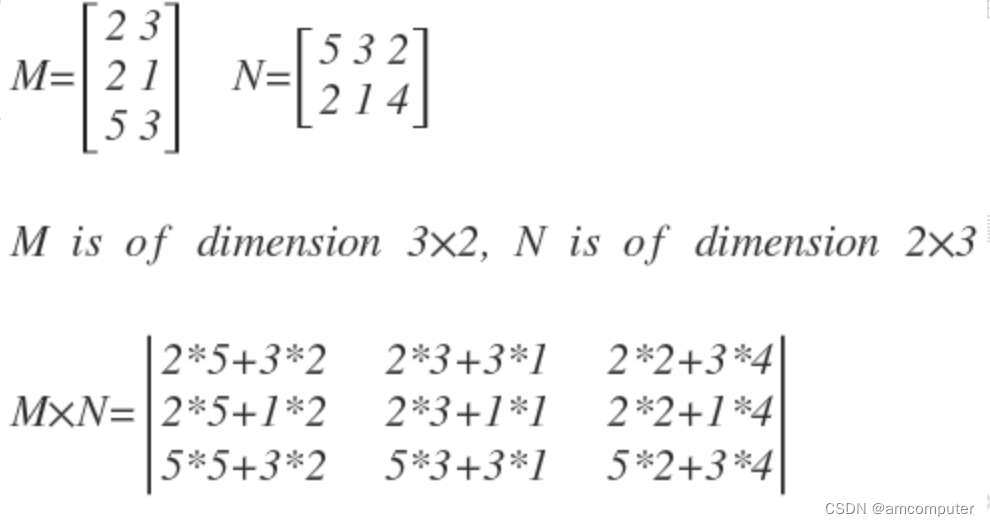
# 1. 对角矩阵的定义和性质**

对角矩阵是一种特殊的方阵，其主对角线以外的所有元素均为零。它具有以下性质：

* **对角元素相等：**主对角线上的所有元素都相等。
* **行列式：**行列式等于主对角线元素的乘积。
* **逆矩阵：**如果主对角线元素均不为零，则逆矩阵存在，且逆矩阵的主对角线元素为原矩阵主对角线元素的倒数。
* **特征值：**特征值等于主对角线上的元素。
* **特征向量：**特征向量为单位向量，其元素为对角线元素的单位向量。

# 2. 对角矩阵的加法和减法**

### 2.1 加法运算

#### 2.1.1 矩阵加法的基本规则

矩阵加法是一种二元运算，它将两个具有相同维度的矩阵相加，得到一个新的矩阵。矩阵加法的基本规则如下：

A + B = C

其中，A、B 和 C 是具有相同维度的矩阵。矩阵 C 的元素 c_ij 等于矩阵 A 的元素 a_ij 和矩阵 B 的元素 b_ij 的和，即：

c_ij = a_ij + b_ij

#### 2.1.2 对角矩阵加法的特殊性

对角矩阵是一种特殊类型的矩阵，其对角线上的元素非零，而其他元素均为零。对于对角矩阵，加法运算具有以下特殊性：

* **对角线上的元素相加：**对角矩阵 A 和 B 相加后，得到的矩阵 C 的对角线上的元素等于矩阵 A 和 B 对角线上的元素之和。
* **非对角线上的元素保持为零：**由于对角矩阵中非对角线上的元素均为零，因此加法运算后，矩阵 C 中的非对角线上的元素仍为零。

### 2.2 减法运算

#### 2.2.1 矩阵减法的基本规则

矩阵减法是一种二元运算，它将一个矩阵从另一个矩阵中减去，得到一个新的矩阵。矩阵减法的基本规则如下：

A - B = C

其中，A、B 和 C 是具有相同维度的矩阵。矩阵 C 的元素 c_ij 等于矩阵 A 的元素 a_ij 和矩阵 B 的元素 b_ij 的差，即：

c_ij = a_ij - b_ij

#### 2.2.2 对角矩阵减法的特殊性

对于对角矩阵，减法运算具有以下特殊性：

* **对角线上的元素相减：**对角矩阵 A 和 B 相减后，得到的矩阵 C 的对角线上的元素等于矩阵 A 和 B 对角线上的元素之差。
* **非对角线上的元素保持为零：**由于对角矩阵中非对角线上的元素均为零，因此减法运算后，矩阵 C 中的非对角线上的元素仍为零。

**示例：**

考虑以下两个对角矩阵：

A = [2 0 0; 0 3 0; 0 0 4]
B = [1 0 0; 0 2 0; 0 0 3]

**加法运算：**

A + B = [2 + 1 0 0; 0 + 2 0; 0 + 0 4] = [3 0 0; 0 5 0; 0 0 7]

**减法运算：**

A - B = [2 - 1 0 0; 0 - 2 0; 0 - 0 4] = [1 0 0; 0 1 0; 0 0 4]

从示例中可以看出，对于对角矩阵，加法和减法运算遵循矩阵加法和减法的基本规则，同时具有对角线上的元素相加或相减的特殊性。

# 3. 对角矩阵的乘法

### 3.1 数乘运算

#### 3.1.1 数乘运算的基本规则

数乘运算，也称为标量乘法，是将一个标量（数字）与一个矩阵相乘。对于对角矩阵，数乘运算遵循以下基本规则：

- 标量乘以对角矩阵后，得到一个新的对角矩阵。
- 新的对角矩阵中每个元素等于原对角矩阵中对应元素乘以标量。

#### 3.1.2 对角矩阵数乘的特殊性

对于对角矩阵，数乘运算具有以下特殊性：

- 对角矩阵数乘运算的结果仍然是一个对角矩阵。