【递归终止条件的重要性】：避免无限递归，确保算法稳定性

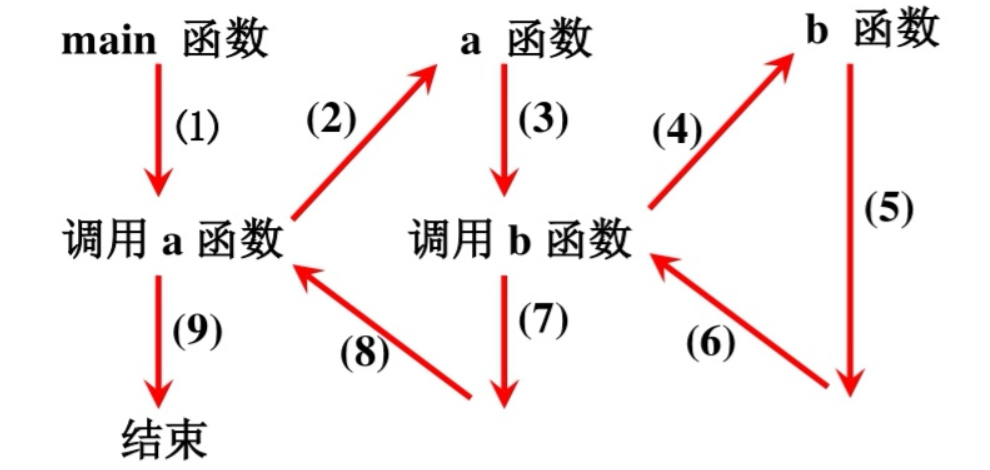
# 1. 递归终止条件概述

递归是计算机科学中的一个重要概念，它通过函数自我调用来解决问题，实现程序的优雅分解。递归算法依赖于终止条件来停止自我调用的无限循环，防止内存溢出并确保程序的正确执行。理解并正确设置递归终止条件对于编写可靠且高效的递归函数至关重要。本章我们将探讨递归终止条件的定义、必要性及其在递归算法中的作用。

# 2. 递归算法的理论基础

## 2.1 递归的概念与结构
### 2.1.1 递归定义与数学基础
递归是计算机科学中一种重要的思想，它允许函数调用自身来解决问题。在数学上，递归关系可以用来定义序列，比如自然数序列、斐波那契数列等。一个递归定义通常包含两个部分：基准情况（base case）和递归情况（recursive case）。

基准情况是递归的最小实例，它可以直接求解，不需要进一步的递归调用。递归情况则是函数调用自身来解决问题的一个更小实例。递归定义的序列通常遵循如下形式：

\[ a_n = f(a_{n-1}, a_{n-2}, ..., a_{n-k}) \]

其中，\(a_n\)是序列的第n项，\(f\)是递归函数，而\(k\)是固定值，表示从前面的几个项来计算当前项。

### 2.1.2 递归算法的工作原理
递归算法通过不断分解问题，将其简化为更小的问题，直到达到基准情况，然后逐级返回，最终解决整个问题。每一个递归调用都增加了调用栈（call stack）的深度，每一个函数调用都需要被记住，以便函数返回时可以继续执行。

例如，考虑计算阶乘的递归函数：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

这里，基准情况是`n == 0`，此时返回值是`1`。递归情况则是当前的`n`乘以`n-1`的阶乘。

## 2.2 递归算法的设计原则
### 2.2.1 确定递归基准情况
设计递归算法时，确定合适的基准情况至关重要。基准情况需要满足以下条件：

- 它必须是一个简单的、明确的问题，可以立即解决。
- 它应当避免无限递归，即不能依赖于自身的进一步递归调用来解决。

### 2.2.2 确保递归逻辑的正确性
递归逻辑需要确保每次递归调用都在朝着基准情况前进。这意味着：

- 递归的每一步都应该简化问题，使问题规模减小。
- 每个递归调用都应该是可解的，不会造成死循环或超时。

## 2.3 递归与迭代的比较
### 2.3.1 递归与迭代的优缺点分析
递归和迭代都是解决问题的常见方法，但它们在实现和性能上有明显的区别：

**递归：**
- **优点：**代码通常更简洁、易读，逻辑清晰。递归在处理自然语言和数据结构（如树和图）时具有优势。
- **缺点：**每次递归调用都会消耗额外的内存（调用栈），可能导致栈溢出。递归方法通常比迭代方法慢。

**迭代：**
- **优点：**通常更快，更节省内存，因为不需要额外的栈空间。
- **缺点：**可能需要更复杂的循环控制逻辑，代码的可读性和可维护性相对较低。

### 2.3.2 如何选择合适的算法实现方式
选择递归还是迭代取决于具体问题的性质和性能要求：

- 如果问题具有自然的递归结构，或者递归可以使代码更简洁，那么递归可能是更好的选择。
- 如果性能是关键考虑因素，特别是当递归深度较大时，迭代可能更合适。
- 在一些情况下，可以将递归算法改写为迭代算法，例如使用尾递归优化技术，减少内存消耗。

递归和迭代各有其适用场景，开发者需要根据具体问题来选择最合适的实现方式。在下一章，我们将探讨递归终止条件的实践应用，包括编写递归函数、错误处理以及优化方法。

# 3. 递归终止条件的实践

## 3.1 编写带有终止条件的递归函数

### 3.1.1 基本示例：计算阶乘

递归是解决可分解为相似子问题的算法设计中不可或缺的工具。考虑计算阶乘的函数，这是一个很自然的递归场景。阶乘 `n!` 表示所有小于或等于 `n` 的正整数的乘积。

下面是一个使用递归计算阶乘的简单示例：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)

print(factorial(5))  # 输出: 120

#### 参数说明和代码逻辑分析

在上述代码中，`factorial` 函数首先检查终止条件 `if n == 0`。这是递归中的基本情况，用于停止递归调用，防止无限循环。一旦 `n` 为0，函数返回1，这是阶乘的数学定义。否则，函数调用自身 `factorial(n - 1)` 并将结果乘以 `n`。

### 3.1.2 进阶示例：二叉树遍历

递归在树结构中的应用非常广泛。以二叉树的中序遍历为例，该过程遵循“左-根-右”的顺序。

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def inorderTraversal(root):
    if root:
        inorderTraversal(root.left)
        print(root.val, end=" ")
        inorderTraversal(root.right)

# 构建示例二叉树:
#     1
#    / \
#   2   3
#  / \
# 4   5

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

inorderTraversal(root)  # 输出: 4 2 5 1 3

#### 递归逻辑的逐行解读分析

在上述 `inorderTraversal` 函数中，每次递归调用都会首先检查当前节点 `root` 是否存在。如果不存在，则返回上一层调用。如果存在，按照中序遍历的顺序，递归遍历左子树，访问根节点，然后递归遍历右子树。函数使用一个简单的打印语句来输出节点值，实际应用中这里可以是任何对节点值的操作。

## 3.2 递归终止条件的错误处理

### 3.2.1 错误的终止条件导致的问题

当递归函数中的终止条件设置不正确时，可能会导致无限递归，最终引发栈溢出错误（Stack Overflow）。这是因为每次递归调用都会占用一定的栈空间，如果递归没有终止条件或条件设置不当，那么递归会无限进行下去，直到耗尽所有的栈空间。

例如，如果将计算阶乘的终止条件写为 `if n > 0`，那么 `n` 永远不会为0，导致无限递归。以下是错误示例：

def incorrect_factorial(n):
    if n > 0:  # 错误的终止条件
        return n * incorrect_factorial(n - 1)
    # 没有处理 n == 0 的情况

# 这将导致无限递归错误
print(incorrect_factorial(5))

### 3.2.2 调试与预防无限递归的技巧

为了预防无限递归，程序设计中应严格检查终止条件是否合理，并且完整覆盖所有可能的情况。通常，可以使用打印语句来追踪递归调用的过程，确定调用栈的每一步操作是否正确。

一个更为系统化的调试方法是使用递归树的方法。递归树可以可视化地展现递归调用的流程，辅助开发者发现和修正错误。

例如，构建一个递归树来展示错误的阶乘函数的递归过程：

graph TD;
    A(incorrect_factorial(5)) -->|n > 0| B(incorrect_factorial(4))
    B -->|n > 0| C(incorrect_factorial(3))
    C -->|n > 0| D(incorrect_factorial(2))
    D -->|n > 0| E(incorrect_factorial(1))
    E -->|n > 0| F(incorrect_factorial(0))