【递归在排序算法中的角色】：快速排序与归并排序中的递归应用

# 1. 排序算法概述与递归基础

排序算法作为计算机科学的核心组成部分，其重要性不言而喻。它们是算法课程和数据结构教学中不可或缺的部分，是理解复杂数据操作的基本工具。在众多排序方法中，递归排序算法因其逻辑的简洁性和效率的优越性而广泛应用。递归是一种方法，它允许函数调用自身来解决问题的子集，这使得复杂问题能够简化为更小、更易管理的实例。

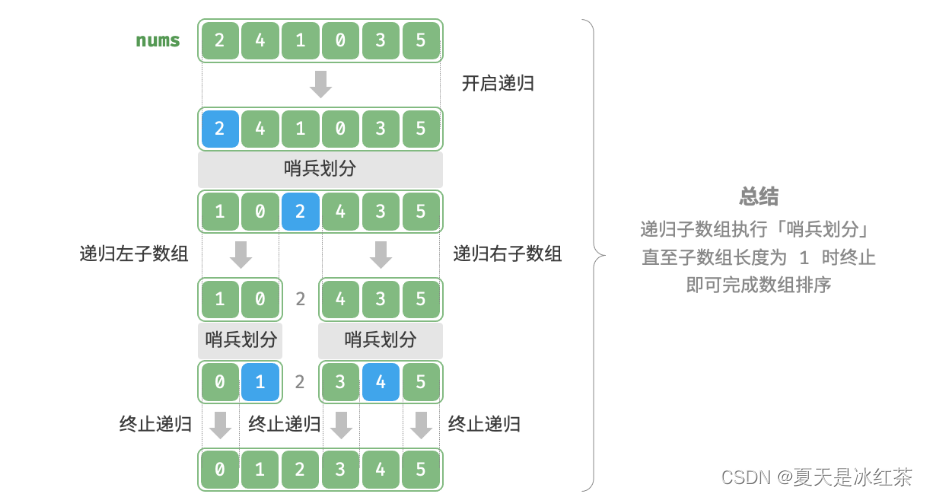
递归方法的一个经典例子是递归排序算法。递归排序算法通常利用分而治之（Divide and Conquer）的策略，将数据集分割成更小的部分，递归地解决这些子问题，最后再合并结果。排序算法中，快速排序（Quick Sort）和归并排序（Merge Sort）是最著名的两种递归排序算法。

在本章中，我们将探讨排序算法的基础知识，理解递归概念，并分析递归如何在各种排序算法中应用。我们会从排序算法的基础开始，逐步深入到递归的定义、工作原理及其与迭代方法的对比，为深入理解后续章节中的排序算法和递归实现打下坚实的基础。

# 2. ```
# 第二章：递归理论及在排序中的应用
递归是计算机科学中一个重要的概念，它指的是一个函数直接或间接地调用自身来解决问题的方法。在排序算法中，递归提供了一种强大的工具来简化问题的解决过程，尤其是在那些具有分治思想的算法中。本章将从递归的基本概念入手，深入分析其在排序算法中的应用及优势。

## 2.1 递归概念解析

### 2.1.1 递归定义与工作原理
递归函数是能够调用自身的函数。它通常包含两个基本部分：基本情况（base case）和递归情况（recursive case）。基本情况是指递归的结束条件，当满足这个条件时，递归不再继续，从而避免无限循环。递归情况则是指函数调用自身的操作，通常伴随着问题规模的缩小。

递归工作原理可以通过一个经典的例子来说明——计算阶乘。计算n的阶乘（记作n!）可以定义为n*(n-1)!，当n为0时，0!定义为1，这时递归停止。用代码表示如下：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

# 调用函数
print(factorial(5))  # 输出为 120

### 2.1.2 递归与迭代的对比分析
递归与迭代是解决循环问题的两种主要方法。迭代通过循环结构重复执行代码块直到满足条件，而递归则是通过函数自身的多次调用来达到循环的效果。在某些情况下，递归能够提供更清晰和简洁的解决方案，尤其是在问题能够自然地分解为更小的子问题时。

然而，递归也有其缺点，比如在深度递归时可能导致栈溢出。迭代通常在空间效率上优于递归，因为迭代不需要额外的函数调用栈空间。从代码可读性上看，递归形式往往更符合人类的直觉思维。

## 2.2 递归在排序算法中的角色

### 2.2.1 排序算法对递归的需求
在分治策略的排序算法中，如快速排序和归并排序，递归是必不可少的。这些算法将问题分解为子问题，并且这些子问题在结构上是相同的，只是规模更小。递归恰好能够自然地表达这种自上而下或自下而上的分解过程。

### 2.2.2 递归在排序算法设计中的优势
递归的设计优势在于它能够简化复杂问题的求解过程。对于排序算法，递归能够将复杂的问题分解成更小的、更容易解决的子问题，并且能够将不同子问题的解决方案合并起来形成最终结果。递归通过减少代码的重复和增强问题的模块化，使得代码更加清晰易懂。

递归的另一个优势是它有助于算法的理论分析。分治算法的递归特性使得其时间复杂度分析能够使用递归树模型来描述，从而得到简洁的数学表达式。此外，递归结构也便于算法的优化，比如通过减少不必要的递归调用来提高效率。

在下一章节中，我们将具体探讨快速排序算法，这是一类特别依赖递归的排序算法，并且我们将详细剖析其递归实现的过程和优化方法。

# 3. 快速排序算法详解与递归实现

## 3.1 快速排序算法原理

### 3.1.1 快速排序的基本步骤

快速排序是一种高效的排序算法，它采用了分治策略对数据集进行排序。基本步骤如下：

1. **选择基准值**：从数组中选择一个元素作为基准值（pivot），通常选择第一个元素、最后一个元素、中间元素或者随机一个元素。
2. **分区操作**：重新排列数组，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆放在基准后面。这个操作称为分区（partitioning）。
3. **递归排序**：递归地将小于基准值元素的子数组和大于基准值元素的子数组排序。

快速排序的这个过程可以用以下伪代码表示：

QUICKSORT(A, low, high)
if low < high then
pivot := PARTITION(A, low, high)
QUICKSORT(A, low, pivot-1)
QUICKSORT(A, pivot+1, high)

在分区操作中，一个常用的分区函数是`Lomuto`分区方案，或者更高效的是`Hoare`分区方案。本文将着重使用`Lomuto`分区方案进行讨论。

### 3.1.2 快速排序的优化策略

快速排序尽管高效，但在实际应用中仍有很多优化策略可以采用：

- **选择更好的基准值**：使用随机选择基准值可以避免在已排序或接近排序的数组上执行最差情况。
- **尾递归优化**：在递归调用中避免不必要的栈开销。
- **三数取中**：取基准值时，可取当前区间的中间三个值的中间值作为基准值。
- **小数组切换到插入排序**：对于小数组，使用插入排序往往更高效。

## 3.2 快速排序的递归实现

### 3.2.1 递归分治法在快速排序中的应用

快速排序的递归实现正是分治法的最佳实践。下面是快速排序算法的递归实现伪代码：

PARTITION(A, low, high)
pivot := A[high]
i := low
for j := low to high-1
if A[j] < pivot then
swap A[i] with A[j]
i := i + 1