LS-DYNA隐式求解:材料模型的智慧选择与应用
发布时间: 2024-12-29 14:02:49 阅读量: 19 订阅数: 26 


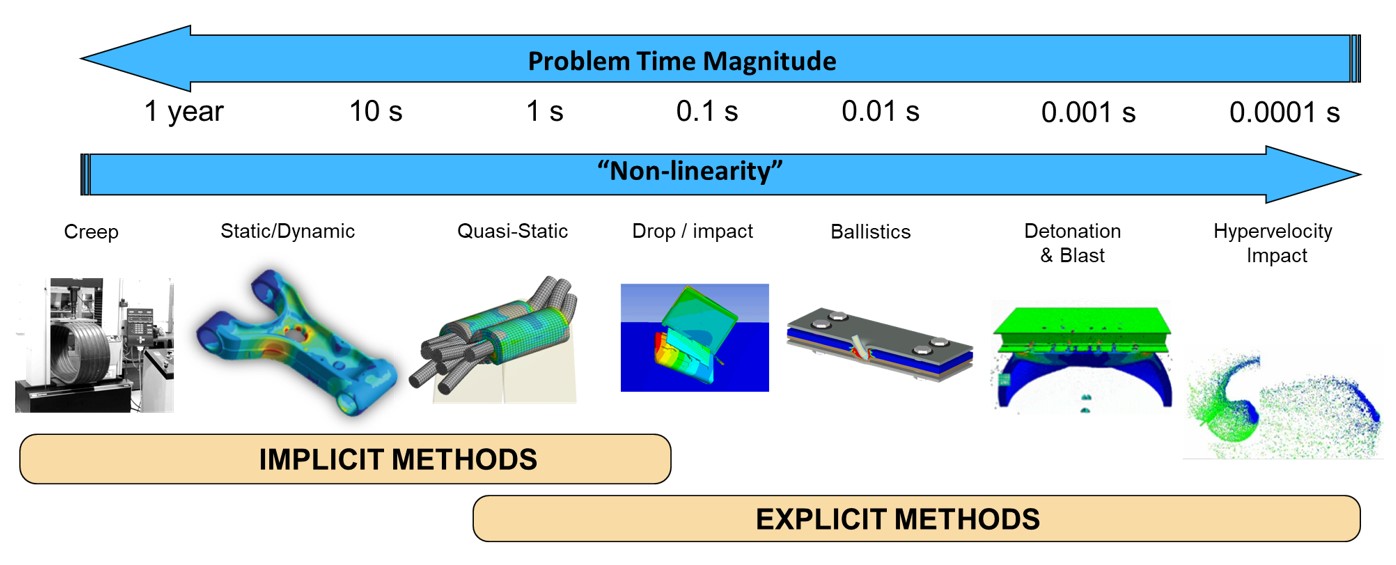
LS-DYNA显示—隐式求解步骤
# 摘要
本文全面阐述了LS-DYNA隐式求解框架下材料模型的基础知识、分类、参数确定以及在实际应用中的表现和优化。首先,介绍了隐式求解的基本理论及其与材料模型的关系,强调了材料模型在提高求解精度和稳定性方面的作用。然后,详细讨论了材料模型的分类及其特点,以及如何通过实验数据和数值模拟确定模型参数。文章进一步通过应用实例,说明了材料模型在隐式求解中处理非线性问题和模拟材料失效时的应用,并提出了针对常见问题的解决方案。优化材料模型以提升求解精度是第四章的重点,其中涵盖了敏感度分析、校准、验证以及多尺度建模技术。最后,展望了材料模型未来的发展趋势,包括智能化、自动化和新型材料模型的开发方向,同时分析了当前面临的挑战与机遇。
# 关键字
LS-DYNA隐式求解;材料模型;参数确定;敏感度分析;多尺度建模;智能化材料模型
参考资源链接:[LS-DYNA隐式求解步骤详解](https://wenku.csdn.net/doc/2jr8n8am8v?spm=1055.2635.3001.10343)
# 1. LS-DYNA隐式求解的基础理解
在现代工程仿真中,隐式求解方法扮演了重要的角色,特别是在涉及到复杂物理现象和长期静态或准静态结构分析的情况下。隐式方法以其稳定性和对大型非线性问题的处理能力而闻名。了解LS-DYNA隐式求解的基础概念对于提高工程设计的质量和预测性能至关重要。本章将简要介绍隐式求解的基本原理,并探讨其在结构分析中的应用。
## 1.1 隐式求解方法概述
隐式求解是数值计算中的一种技术,用于解决线性或非线性的常微分方程或偏微分方程。在有限元分析(FEA)中,隐式求解通过迭代方法来预测结构在受力状态下的响应。隐式算法通常采用牛顿-拉夫森方法或修正的牛顿方法进行迭代,以达到平衡状态。
## 1.2 隐式求解与显式求解的区别
与隐式求解不同,显式求解方法更适合于瞬态动力学分析,如碰撞、爆炸和冲击波传播问题。显式求解使用时间步长,并在每个时间步长内求解运动方程,而隐式求解则直接求解整个时间范围内的方程组。这两种方法各有优缺点,并适用于不同的工程问题。
## 1.3 隐式求解在工程仿真中的应用
隐式求解在工程仿真中的应用包括但不限于汽车碰撞模拟、金属成型、结构稳定性分析等。通过这种求解方法,工程师能够预测和分析结构在各种静态或缓慢变化负载下的表现,从而优化产品设计和性能。在本章的后续部分,我们将探讨隐式求解的更多细节及其在材料模型中的应用。
# 2. 材料模型的定义与重要性
### 材料模型在有限元分析中的角色
有限元分析(FEA)是现代工程设计和产品开发的重要工具,其中材料模型扮演着至关重要的角色。通过材料模型,工程师可以在计算机上模拟材料在不同环境和负载条件下的行为。这使得在实际制造或测试之前,可以预测产品或结构的性能和可靠性。例如,在设计汽车时,通过有限元分析可以评估在撞击时车身各部分的变形情况和材料的反应,从而在没有物理原型的情况下优化设计。
### 不同材料模型的特点和适用领域
在有限元分析中,存在多种材料模型以适应不同类型的材料和应用需求。例如,对于金属材料,塑性模型和弹性模型是常见的选择,因为它们能够描述材料在超过屈服点后的永久变形行为。而复合材料模型则用于模拟纤维增强复合材料,它们可以考虑纤维方向的各向异性特性。对于生物医学应用,粘弹性模型用来描述软组织如皮肤或心脏瓣膜的动态响应。
## 材料模型的分类详解
### 弹性材料模型
弹性材料模型基于胡克定律,假设材料在加载和卸载过程中变形是完全可逆的,不存在永久变形。简单来说,一旦外部载荷去除,材料将恢复到其原始形状。这种模型适用于描述金属在弹性范围内的行为,如钢和铝等。弹性模型往往用于初步设计阶段,因为它计算效率较高,易于实现。
### 塑性材料模型
塑性材料模型则考虑了材料变形中的永久形变。当应力超过材料的屈服极限时,塑性模型能够模拟材料在卸载后不完全恢复原状的现象。这在金属加工和金属成型模拟中尤其重要,例如冷轧钢板的制造过程。塑性模型的复杂性通常高于弹性模型,因为需要考虑如硬化法则、屈服准则等更多的行为描述。
### 粘弹性与复合材料模型
粘弹性材料模型结合了弹性和粘性的特性,常用于模拟聚合物等具有时间依赖性的材料。例如,在汽车内饰设计中,用此模型来评估材料在长期负荷作用下的性能退化。复合材料模型则考虑到材料的各向异性,这类模型特别适用于航空和汽车工业中用到的先进复合材料。复合材料模型对于准确预测材料在复杂负载作用下的应力分布至关重要。
## 材料模型参数的确定方法
### 实验数据获取和参数拟合
确定材料模型参数的第一步通常是通过实验获取必要的材料特性数据。这些数据可能包括应力-应变曲线、蠕变测试结果、疲劳寿命等。获得这些数据后,可以采用各种数值拟合技术,如最小二乘法,来确定材料模型的最佳参数。参数拟合过程需要确保模型预测与实验数据之间误差最小化。
### 数值模拟中的材料参数验证
在参数确定后,需要在数值模拟环境中验证这些参数。这涉及在特定的有限元软件中实现模型,并进行一系列模拟,然后将模拟结果与实验结果进行比较。如果发现偏差,可能需要重新调整参数,直到模拟结
0
0





