【LS-DYNA隐式求解深度剖析】:接触问题的定义与处理
发布时间: 2024-12-29 14:08:47 阅读量: 17 订阅数: 12 


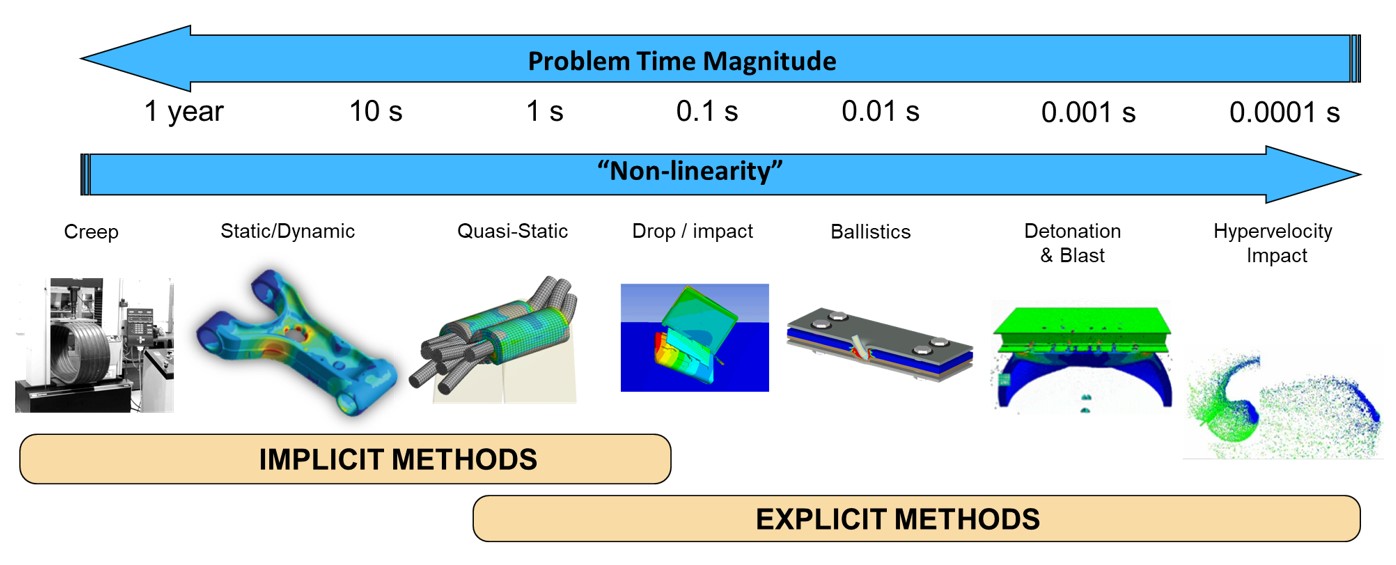
LS-DYNA显示—隐式求解步骤
# 摘要
LS-DYNA作为一款先进的有限元分析软件,其隐式求解器在处理接触问题时具有独特的优势。本文首先概述了LS-DYNA隐式求解的基本原理,随后深入探讨了接触问题的理论基础,包括定义、分类、力学行为、理论模型及其数值稳定性。第三章着重介绍了LS-DYNA隐式求解中接触功能的集成、参数设置以及收敛性问题的处理。第四章探讨了复杂接触问题的高级处理技巧,包括建模策略、高级算法应用和后处理分析。第五章通过案例分析,展现了接触问题在工程应用中的模拟步骤、问题诊断及优化策略。最后,本文总结了接触问题处理的关键点,并对未来的研究方向和接触问题的发展前景进行了展望。
# 关键字
LS-DYNA;隐式求解;接触问题;数值稳定性;高级算法;案例分析;后处理分析
参考资源链接:[LS-DYNA隐式求解步骤详解](https://wenku.csdn.net/doc/2jr8n8am8v?spm=1055.2635.3001.10343)
# 1. LS-DYNA隐式求解概览
## 1.1 隐式求解的基本概念
LS-DYNA作为一个强大的有限元分析软件,它支持显式和隐式两种求解方法。隐式求解,又称为静态求解,主要适用于求解静态和准静态问题。与显式求解相比,隐式求解更适合于分析在达到平衡状态前需要经过长时间过程的复杂结构问题。
## 1.2 隐式求解的特点和应用
隐式求解算法的核心是基于牛顿-拉夫森迭代方法,其特点在于能够高效求解具有高度非线性特征的问题,且对时间步长的敏感性较低。在实际工程中,这种求解方法被广泛应用于结构静力学、热传导、多物理场耦合等领域的模拟分析。
## 1.3 隐式求解的求解流程
隐式求解流程通常包括建立数学模型、网格划分、定义边界条件和材料属性、选择适当的求解器并设定求解参数,最后进行迭代求解直至满足收敛条件。在LS-DYNA中,进行隐式求解前,需要特别注意模型的建模质量和参数选择,这些因素对于求解过程和结果的准确性至关重要。
隐式求解方法在工程应用中需要根据问题特性选择合适的求解器,进行精细的模型设置,并严格控制计算精度以获取正确的分析结果。下一章节将详细探讨接触问题在有限元分析中的角色及其理论基础。
# 2. 接触问题理论基础
在有限元分析(FEA)中,接触问题是一个极其复杂且关键的研究领域。当物体相互作用时,接触面的力学行为会直接影响整个结构的响应。因此,理解和处理接触问题对于确保仿真结果的精确性至关重要。在本章中,我们将深入探讨接触问题的基础理论,为后续章节中LS-DYNA隐式求解器中的具体应用打下坚实的基础。
## 2.1 接触问题在有限元分析中的角色
### 2.1.1 接触问题的定义和分类
接触问题在有限元分析中定义为两个或多个刚性或柔软体之间的边界相互作用。这种相互作用不仅包括了物体表面之间的直接接触,还涉及由接触引起的力的传递。在实际问题中,接触可能发生在多种情形,如刚体之间的碰撞、弹性体之间的压缩或滑动等。
接触问题主要分为两类:面-面接触和点-面接触。面-面接触涉及到物体的两个相对较大的表面之间的相互作用,而点-面接触则涉及到更小尺寸的区域,例如在尖锐物体与平面之间的接触。为了简化问题并提高计算效率,工程实践中常将复杂的接触问题转化为更易处理的类型。
### 2.1.2 接触界面的力学行为
接触界面的力学行为非常复杂,涉及接触面的粘附、滑移、摩擦以及可能的材料损伤。在理想情况下,接触界面不允许物体相互穿透,必须满足不可穿透条件。同时,接触表面可能施加法向力和切向力,法向力处理了物体的压缩和分离行为,而切向力则与摩擦系数相关,反映了接触面间的滑动行为。
## 2.2 接触算法的理论模型
### 2.2.1 接触面的识别技术
接触面的识别技术是有限元分析中的一项关键技术。它涉及到如何高效地确定在任意时刻,哪些元素和节点处于接触状态。典型的识别技术包括基于节点的算法和基于面的算法。节点-面算法是通过检测一个体的节点是否进入了另一体的面来确定接触,而面-面算法则是基于两个体的接触面之间的穿透深度来判断。
### 2.2.2 接触力的计算方法
接触力的计算方法多种多样,其中包括拉格朗日乘子法、罚函数法以及增强拉格朗日乘子法等。罚函数法是一种常用的接触力计算方法,通过施加一个足够大的“罚”参数来防止物体间的穿透,并计算由此产生的接触力。这种方法简洁但对罚参数的选择非常敏感,选择不当可能会导致数值不稳定性。
### 2.2.3 接触刚度的确定
接触刚度是影响接触计算精度的关键因素。它反映了接触面之间抵抗穿透的能力。理论上,接触刚度越大,计算结果越准确。但在实际计算中,过高的接触刚度可能会引起数值问题,如“锁定效应”,即材料的过度刚化。因此,确定一个适中的接触刚度对于保证计算精度和稳定性至关重要。
## 2.3 接触问题的数值稳定性
### 2.3.1 时间步长的影响
在动态接触问题中,时间步长的选择对于数值稳定性和求解精度至关重要。一般来说,时间步长越小,计算结果越精确,但同时计算成本也会越高。时间步长的选择需要平衡这两个因素。通常,时间步长应小于由材料的最大声速决定的稳定性限制。
### 2.3.2 摩擦模型对稳定性的影响
摩擦模型的选择对于接触问题的数值稳定性也有很大影响。对于干燥接触,采用简单的库伦摩擦模型就足够了。而在需要更精确地描述接触面间相对滑动行为时,可以采用更复杂的摩擦模型,如粘滑摩擦模型。然而,更复杂的摩擦模型也会引入更多的计算复杂度,可能影响到整体的数值稳定性。
为了深入理解这些概念,我们可以举一个简化的二维接触问题的例子。例如,考虑一个滑块沿着一个固定表面的运动,其中滑块和表面之间有摩擦力的作用。通过使用有限元软件,比如ANSYS或ABAQUS进行模拟,我们可以观察到不同接触算法和参数设置下,滑块的加速度和摩擦力的变化情况。
```mermaid
graph TD
A[开始接触分析] --> B[确定接触面]
B --> C[选择接触算法]
C --> D[计算接触力]
D --> E[调整接触刚度]
E --> F[选择时间步长]
F --> G[选定摩擦模型]
G --> H[运行有限元分析]
H --> I[结果分析与验证]
```
在上述流程图中,我们可以看到接触分析的一系列步骤,从接触面的确定到摩擦模型的选择,再到最终的分析结果验证,每一步都是保证仿真结果准确性的重要环节。通过理解这些步骤,工程师可以更加精确地模拟真实世界中的接触问题,为产品的设计和优化提供有力的支持。
通过本章的介绍,我们对接触问题的基础理论有了初步了解。在下一章中,我们将深入探讨在LS-DYNA隐式求解器中如何具体设置和处理接触问题。
# 3. LS-DYNA隐式求解中的接触处理
## 3.1 LS-DYNA隐式求解器接触功能概览
### 3.1.1 接触模块的集成和应用
LS-DYNA作为一款先进的有限元分析软件,其隐式求解器中的接触模块是模拟复杂动态过程中的关键组件。接触模块的集成允许用
0
0





