LS-DYNA隐式求解:非线性问题,策略先行
发布时间: 2024-12-29 14:12:34 阅读量: 44 订阅数: 26 


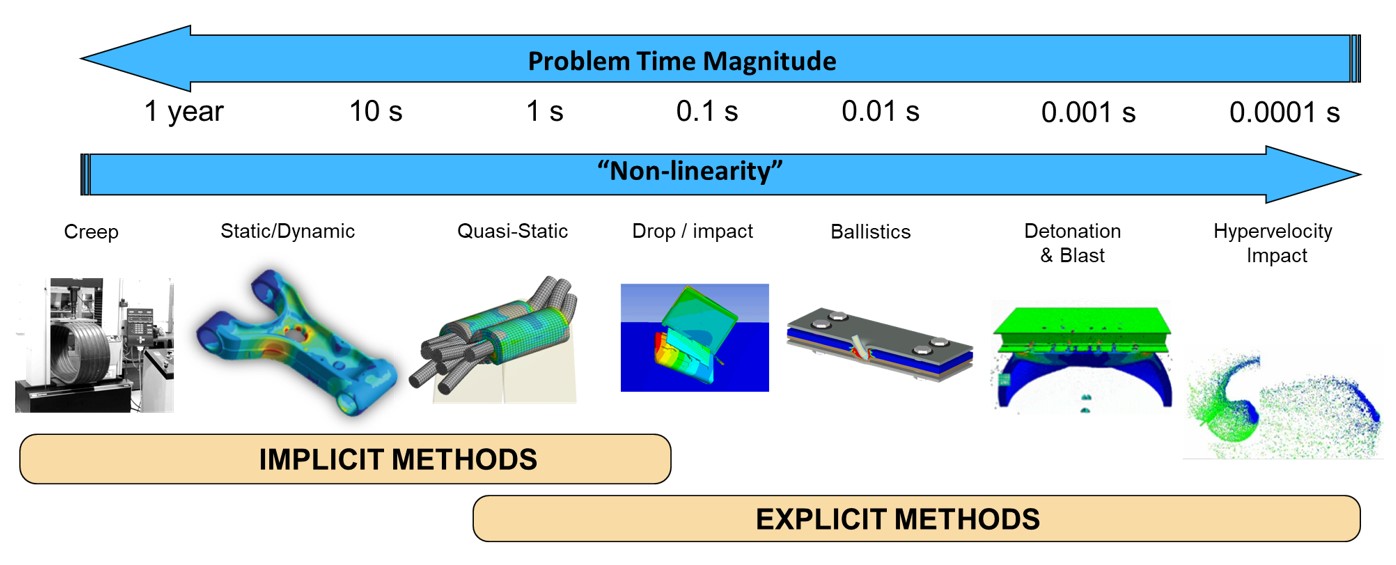
LS-DYNA显示—隐式求解步骤
# 摘要
LS-DYNA是一款广泛应用于非线性动态分析的仿真软件,其隐式求解器在处理静态和稳态问题时展现出独特的优点。本文从隐式求解的理论基础出发,详细介绍了隐式求解与显式求解的主要区别及其适用场景。文中深入探讨了非线性问题的理论分析和数值求解方法,包括牛顿-拉夫森迭代方法和线性方程组的求解技术。随后,本文分享了在实际操作中模型准备、材料参数设定、载荷与边界条件施加等实践技巧,并探讨了求解策略的选择和调整。最后,通过工程案例分析以及非线性求解策略的综合应用,本文提出了有效的策略优化方法,并对求解过程中的问题诊断与解决方案进行了探讨,旨在为使用LS-DYNA进行隐式求解的研究者和工程师提供全面的参考。
# 关键字
LS-DYNA;隐式求解;非线性问题;数值方法;策略优化;案例分析
参考资源链接:[LS-DYNA隐式求解步骤详解](https://wenku.csdn.net/doc/2jr8n8am8v?spm=1055.2635.3001.10343)
# 1. LS-DYNA隐式求解概述
## 1.1 LS-DYNA隐式求解简介
LS-DYNA隐式求解是一种数值分析方法,广泛应用于工程领域中复杂结构的静态和稳态动力学问题的仿真。隐式求解以其较高的稳定性、准确性和对复杂材料模型的良好适应性,成为结构分析中不可或缺的一部分。本文将对隐式求解的基础知识和应用实践进行深入探讨,帮助读者掌握其核心原理与操作技巧。
## 1.2 隐式求解的应用前景
随着计算技术的发展,隐式求解方法在各个领域,如汽车碰撞安全、航空结构设计、生物医学工程等,都有其特定的使用场景。它的优势在于处理复杂载荷、多材料接触、大变形等问题时,能够提供更为精确的模拟结果。通过理解隐式求解的原理和优化技巧,工程师和技术人员能够更有效地解决实际工程问题,提高产品的设计质量和安全性。
通过接下来的章节,我们将详细介绍隐式求解的理论基础和实践技巧,并结合案例分析,深入讨论其在非线性问题求解中的应用。
# 2. 隐式求解的理论基础
在上一章节中,我们对LS-DYNA隐式求解进行了宏观层面的介绍。本章节,我们将深入探究隐式求解的理论基础,为实际操作提供坚实的理论支撑。
## 2.1 隐式求解与显式求解的区别
### 2.1.1 求解器类型的基本对比
隐式求解器和显式求解器是两种不同的数值求解器,在解决问题的类型、稳定性、计算速度等方面各有特点。为了更好地理解隐式求解,我们首先对比两种求解器的基本差异。
隐式求解器通过牛顿-拉夫森迭代法或者修正的牛顿法进行求解,而显式求解器通常采用中心差分法。在稳定性方面,隐式求解器通常能够处理更广范围的稳定时间步长,特别是对于刚度较大的系统,而显式求解器则需要非常小的时间步长,但计算速度快,适合求解如碰撞和爆炸等快速动态问题。在收敛性上,隐式求解器在处理非线性问题时具有更好的收敛性,但计算成本相对较高。
### 2.1.2 隐式求解的适用场景
了解了求解器类型的基本对比之后,我们需要明确隐式求解适合应用于哪些具体场景。通常,隐式求解适用于如下情况:
- 求解结构静力学问题
- 求解低速动力学问题,例如缓慢的加载过程
- 需要考虑材料非线性和几何非线性的情况
- 涉及接触和摩擦的复杂相互作用
- 需要精确计算静态位移、应力以及局部化变形
## 2.2 非线性问题的理论分析
### 2.2.1 非线性问题的数学描述
非线性问题在数学上通常表现为方程中未知数的高次项或非线性项,导致方程的解呈现出比线性问题更复杂的特性。一个典型的非线性问题的数学描述如下:
$$ F(u) = K(u)u - f(u) = 0 $$
其中,$F(u)$表示非线性方程,$K(u)$是随着解的变化而变化的刚度矩阵,$f(u)$是载荷向量。非线性问题的解析解通常是不可得的,因此需要依赖数值方法进行求解。
### 2.2.2 材料非线性与几何非线性的处理
处理材料非线性通常涉及到复杂的材料模型,包括塑性、蠕变、断裂等行为的描述,这些都是影响结构响应的重要因素。在LS-DYNA中,可以通过定义本构关系和相应的材料参数来描述材料非线性。
几何非线性通常涉及到结构的大变形问题,例如拉伸、弯曲等,会导致结构刚度发生变化,从而影响结构的响应。LS-DYNA中的隐式求解器可以考虑几何非线性的影响,通过更新几何配置来更准确地捕捉结构响应。
## 2.3 数值求解方法的介绍
### 2.3.1 牛顿-拉夫森迭代方法
牛顿-拉夫森迭代方法是隐式求解中常用的一种数值求解方法,它通过构建泰勒级数展开式并进行线性化处理来逐步逼近真实解。在每一步迭代中,牛顿法都需要求解线性方程组:
$$ K(u^{(i)})\Delta u^{(i)} = -F(u^{(i)}) $$
其中,$K(u^{(i)})$表示在第$i$次迭代时的切线刚度矩阵,$\Delta u^{(i)}$表示第$i$次迭代的增量解,$F(u^{(i)})$为残差向量。
### 2.3.2 线性方程组的求解技术
求解上述线性方程组是隐式求解中的关键步骤之一,常用的求解技术包括直接法和迭代法。直接法如LU分解、Cholesky分解等,能够一次性求得精确解,适用于问题规模较小的情况。而迭代法则如共轭梯度法、雅可比法等,适合大规模问题,尤其是在稀疏矩阵求
0
0





