【LS-DYNA隐式求解精度提升】：模拟优化的专家技巧


# 摘要
LS-DYNA作为一个广泛使用的非线性有限元分析软件，在复杂系统仿真中扮演着重要角色。本文首先概述了LS-DYNA隐式求解方法的基础理论及其与显式求解的区别，接着深入探讨了提升隐式求解精度的实践技巧，包括模型简化、网格质量控制、精确的材料模型和本构关系设置以及边界条件和接触定义的优化。文章还介绍了一系列高级调试技术，包括日志文件分析、求解器参数调优和结果验证。通过案例研究，展示了在复杂系统隐式分析中的具体应用，最后对未来LS-DYNA隐式求解技术的发展趋势进行了展望，包括最新算法的介绍、与其他仿真软件的比较以及为用户提供的专家建议。

# 关键字
LS-DYNA；隐式求解；模型简化；网格质量；材料本构；参数调优

参考资源链接：[LS-DYNA隐式求解步骤详解](https://wenku.csdn.net/doc/2jr8n8am8v?spm=1055.2635.3001.10343)
# 1. LS-DYNA隐式求解概述

## 1.1 引言
LS-DYNA作为一款先进的有限元分析软件，广泛应用于汽车、航空航天、生物力学和消费电子等行业。它的隐式求解器提供了一种高效而精确的数值仿真解决方案，特别是在处理高度非线性问题和静态分析方面。隐式求解器对于复杂的动力学响应和结构稳定性分析尤其重要，其应用范围从简单的静态分析到高度复杂的动态问题。

## 1.2 隐式求解的优势
隐式求解器相较于传统的显式求解器，能够处理更加复杂和精细的网格模型，适用于稳定时间步长的长时程分析。其稳定性好，精度高，能够有效避免显式求解中可能遇到的临界时间步长限制问题。特别在解决如金属成型、接触和摩擦等非线性问题上，隐式求解器显示出了其独特的优势。

## 1.3 应用场景分析
隐式求解主要应用于以下几个典型场景：
- 结构分析：如汽车碰撞安全性评估、航空结构件的设计验证等。
- 接触问题：如齿轮啮合、装配过程模拟、多体系统的动态分析等。
- 稳态分析：如热应力分析、材料成型过程中的流体-结构相互作用等。

以上内容仅为第一章的内容概述，为读者提供了一个关于LS-DYNA隐式求解基础概念和重要性的入门介绍。后续章节将深入探讨其理论基础、求解精度提升、调试技巧、实际案例研究及未来的发展趋势。

# 2. 理论基础与隐式求解原理

### 2.1 隐式动态分析的理论背景

隐式动态分析是一种用于模拟结构动态响应的数值方法，它在工程领域中占有重要地位。为了深入理解隐式求解器的工作原理，我们首先需要探讨动力学分析的基本方程。

#### 2.1.1 动力学分析的基本方程

在结构动力学中，常见的基本方程是牛顿第二定律，表达为：

F = m * a

其中F代表力，m代表质量，而a是加速度。在连续介质力学中，这个关系被推广到任意微元体上，形成控制方程。这些方程通常是偏微分方程，描述了材料的运动和变形状态。在离散化过程中，连续系统被划分为有限的元素，并在节点处施加相应的载荷。

在隐式求解中，主要考虑的是在给定的时刻，如何求解结构响应。相对于显式求解器，它使用迭代的方法求解当前时刻的响应，并依赖于之前的状态来预测未来的动态行为。这使得隐式求解器在处理非线性问题，如塑性变形和接触问题时更加稳定。

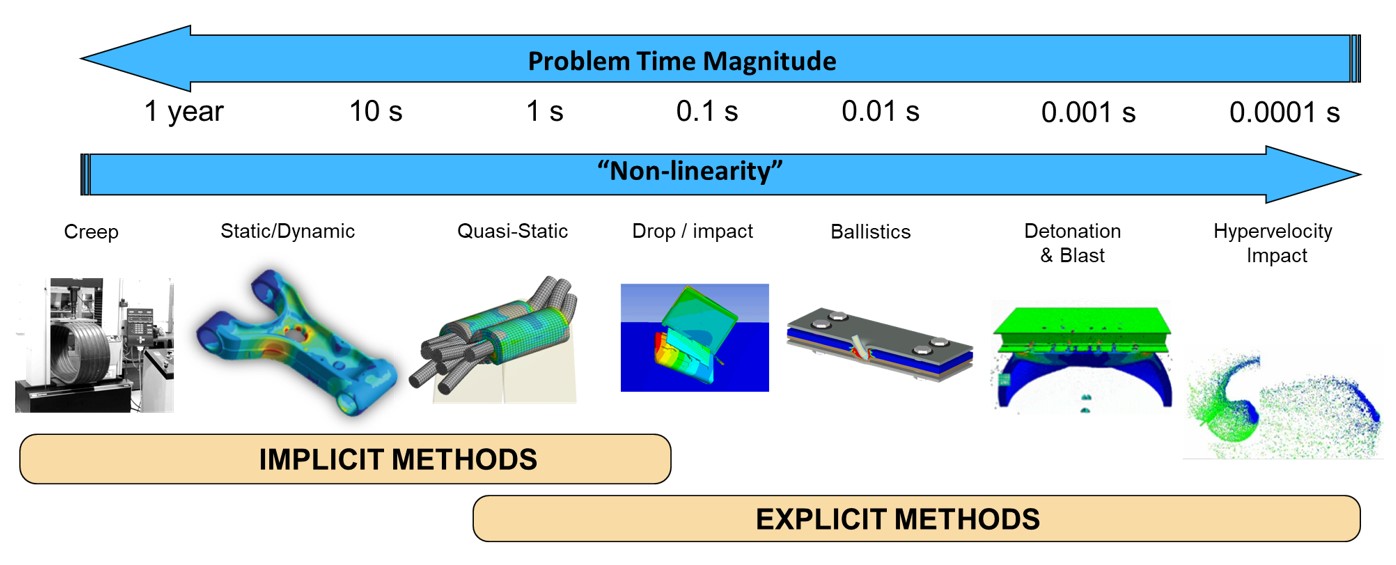
#### 2.1.2 隐式算法与显式算法的区别

隐式算法与显式算法在动力学求解中具有根本的不同。显式算法是时间向前的推进方式，每一步计算的结果只依赖于上一步的状态，因此稳定性较差，但它在处理冲击和爆炸等问题时具有优势。隐式算法则是通过迭代求解系统方程，在每一步计算时考虑系统当前和未来状态的关系。

在隐式求解器中，通常使用牛顿-拉夫森迭代法来求解非线性方程。这种方法通过求解线性化方程组来逐步逼近精确解，对非线性系统的求解提供了良好的稳定性和高精度。

### 2.2 隐式求解器的工作机制

了解了基本的理论背景之后，我们将探讨隐式求解器的工作机制。隐式求解器的核心在于时间积分方案和求解器收敛性的关键因素。

#### 2.2.1 时间积分方案

时间积分方案是隐式求解器的核心组成部分。它负责将时间连续的动态方程离散化为时间步长上的离散值。常见的隐式时间积分方法包括Newmark方法、Wilson-θ方法和HHT-α方法。

以Newmark方法为例，它将位移和速度以线性或非线性方式与时间积分联系起来。该方法的关键在于选择合适的时间步长，确保数值解的稳定性和准确性。时间步长太大可能会导致结果不稳定，太小则会增加计算成本。

#### 2.2.2 求解器收敛性的关键因素

隐式求解器的收敛性与其算法的实现细节紧密相关。为了提高求解器的收敛性，通常需要考虑以下几个关键因素：

- 合适的初始猜测值：一个好的初始猜测值可以加速迭代过程，并提高收敛速度。
- 正确的迭代策略：选择合适的迭代方法（例如直接法或预处理共轭梯度法）可以有效降低迭代次数。
- 参数设置：例如在Newmark方法中，需要适当地设置参数如积分常数、质量矩阵等，这些都会影响求解器的稳定性和收敛性。

此外，材料的非线性行为、复杂的边界条件、接触问题等都是影响隐式求解器收敛性的因素。

### 2.3 精度控制与误差分析

在使用隐式求解器进行动态分析时，需要关注模拟结果的精度控制以及可能产生的误差分析。

#### 2.3.1 时间步长与空间离散化的影响

时间步长的选择直接影响到求解过程的精度和稳定性。较短的时间步长可以提供更高的时间精度，但会增加计算成本。在实际应用中，时间步长的选择需要平衡精度和效率。

空间离散化指的是在结构模型上创建网格，并对每个单元进行求解。网格的质量（如单元形状、大小一致性）直接影响模拟结果的精度。过度细化的网格会增加计算量，而过于粗糙的网格则可能导致结果误差。

#### 2.3.2 结果误差的来源和类型

结果误差主要包括数值误差、模型误差和测量误差。数值误差通常来自于时间积分的近似处理，模型误差可能来源于材料参数和本构模型的不准确设定。测量误差涉及实验数据的准确性，可能影响模型参数的校准。

为了控制这些误差，需要进行细致的网格划分，合理选择材料模型和本构参数，以及谨慎地施加边界条件和载荷。此外，对结果进行敏感性分析和验证，也是确保精度的重要手段。

为了确保精度，可以采用误差控制指标，例如能量守恒定律，来校验模型是否正确反映了物理现象。通过对比实验数据和模拟结果，可以评估模型的适用性和结果的准确性。

以上内容详细介绍了隐式求解的基础理论以及求解过程中的关键因素和误差分析，为之后章节中关于提升求解精度的实践技巧和高级调试技术提供了坚实的理论基础。接下来，我们将深入探讨如何应用这些理论知识来优化LS-DYNA隐式求解的精度。

# 3. 提升LS-DYNA隐式求解精度的实践技巧

## 3.1 模型简化与网格质量控制

### 3.1.1 网格划分的最佳实践

在LS-DYNA中进行隐式求解时，网格质量直接影响求解的精度与效率。模型的网格划分应当考虑几何特征、材料属性以及载荷条件，以确保网格划分能够有效模拟问题的物理行为。

高质量的网格划分应该遵循以下最佳实践：

1. **均匀性**：网格在空间分布上应尽可能均匀，避免出现过大的尺寸变化，这有助于减少数值误差。
2. **形状**：优先使用高质量的元素形状，如四边形和平面三