探索MATLAB傅里叶变换的高级应用：频谱分析和图像重建

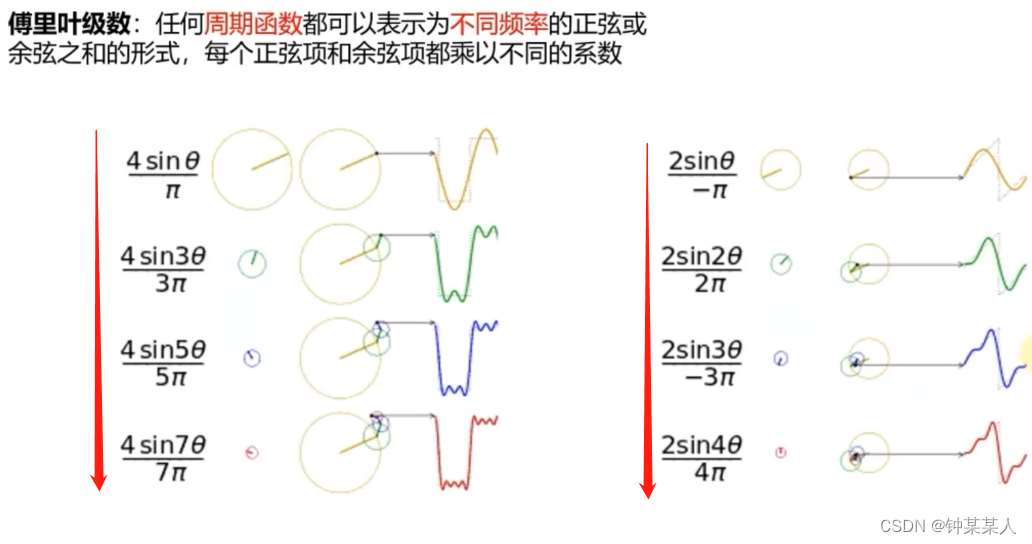
# 1. MATLAB傅里叶变换概述

傅里叶变换是一种数学工具，用于将时域信号分解为其频率分量。它在信号处理、图像处理和量子力学等领域有着广泛的应用。

在MATLAB中，傅里叶变换可以通过`fft`函数实现。该函数接收一个时域信号作为输入，并返回一个包含频率分量的复数数组。复数数组的实部和虚部分别表示幅度和相位。

傅里叶变换的逆变换是逆傅里叶变换，可以通过`ifft`函数实现。逆傅里叶变换将频率分量重新合成回时域信号。

# 2. 傅里叶变换在频谱分析中的应用

### 2.1 频谱分析的基本原理

#### 2.1.1 傅里叶变换的定义和性质

傅里叶变换是一种数学工具，可以将时域信号分解为其频率分量。它将一个函数从时域变换到频域，揭示了信号中不同频率分量的幅度和相位信息。

傅里叶变换的定义如下：

X(f) = ∫_{-\infty}^{\infty} x(t) e^(-i2πft) dt

其中：

* `x(t)` 是时域信号
* `X(f)` 是频域信号
* `f` 是频率
* `i` 是虚数单位

傅里叶变换具有以下性质：

* **线性性：**傅里叶变换是一个线性算子，即对时域信号进行线性操作，其傅里叶变换也进行相应的线性操作。
* **时移不变性：**时域信号的时移不会改变其傅里叶变换，只会引起相位偏移。
* **卷积定理：**时域信号的卷积运算对应于频域信号的乘法运算。

#### 2.1.2 频谱图的解读

频谱图是傅里叶变换的结果，它显示了信号在不同频率下的幅度和相位信息。

* **幅度谱：**表示信号中不同频率分量的幅度，反映了信号的能量分布。
* **相位谱：**表示信号中不同频率分量的相位，反映了信号的时序关系。

通过分析频谱图，我们可以识别信号中的特征频率、谐波分量和噪声成分，从而获得信号的频域特性。

### 2.2 傅里叶变换在信号处理中的应用

#### 2.2.1 噪声滤波

傅里叶变换可以用于从信号中滤除噪声。噪声通常具有宽带分布，而信号通常具有特定频率范围。通过在频域中选择性地滤除噪声频率，我们可以保留信号的有效成分。

#### 2.2.2 特征提取

傅里叶变换还可以用于从信号中提取特征。信号的特征频率可以反映信号的类型、状态或故障模式。通过分析频谱图，我们可以识别和提取这些特征频率，从而实现信号的分类、识别和诊断。

% 信号生成
t = 0:0.01:1;
x = sin(2*pi*10*t) + sin(2*pi*30*t) + randn(size(t));

% 傅里叶变换
X = fft(x);

% 幅度谱
magnitude_spectrum = abs(X);

% 相位谱
phase_spectrum = angle(X);

% 绘制频谱图
figure;
subplot(2,1,1);
plot(magnitude_spectrum);
title('幅度谱');
subplot(2,1,2);
plot(phase_spectrum);
title('相位谱');

**代码逻辑分析：**

* `fft` 函数执行傅里叶变换，将时域信号 `x` 转换为频域信号 `X`。
* `abs` 函数计算复数 `X` 的幅度，得到幅度谱 `magnitude_spectrum`。
* `angle` 函数计算复数 `X` 的相位，得到相位谱 `phase_spectrum`。
* 绘制幅度谱和相位谱，显示信号的频域特性。

# 3.1 图像重建的基本原理

#### 3.1.1 图像傅里叶变换

图像傅里叶变换将图像从空间域转换为频域。在频域中，图像的各个频率分量以复数的形式表示。图像傅里叶变换的公式如下：

F(u, v) = ∫∫f(x, y)e^(-j2π(ux + vy))dxdy

其中：

* `f(x, y)` 是空间域中的图像
* `F(u, v)` 是频域中的图像
* `u` 和 `v` 是频域中的频率变量

#### 3.1.2 图像逆傅里叶变换

图像逆傅里叶变换将图像从频域转换回空间域。图像逆傅里叶变换的公式如下：