递归算法的艺术：掌握递归技巧，解决复杂问题

# 1. 递归算法的理论基础

递归是一种算法设计技术，它允许函数调用自身。理解递归算法需要掌握以下理论基础：

* **递归函数的结构：**递归函数通常由两个部分组成：基线条件和递归调用。基线条件指定函数何时停止递归，而递归调用指定函数如何调用自身。
* **递归函数的终止条件：**基线条件至关重要，因为它确保递归不会无限进行。基线条件通常检查特定输入条件，如果满足，则函数停止递归。
* **递归函数的调用方式：**递归函数可以以直接递归（函数直接调用自身）或间接递归（函数通过其他函数调用自身）的方式调用。

# 2. 递归算法的编程技巧

### 2.1 递归函数的设计和实现

#### 2.1.1 递归函数的结构和调用方式

递归函数是一种以自身为调用目标的函数，其结构通常包含以下两部分：

- **基线条件：** 递归函数的终止条件，当满足基线条件时，函数直接返回结果，不再进行递归调用。
- **递归调用：** 函数自身调用自身，并传递必要的参数，以解决规模更小的问题。

递归函数的调用方式如下：

def recursive_function(parameter):
    # 基线条件
    if condition:
        return result

    # 递归调用
    return recursive_function(parameter_modified)

#### 2.1.2 递归函数的终止条件

递归函数的终止条件至关重要，它确保函数不会陷入无限递归。终止条件通常是基于问题规模的递减，例如：

- **数组长度：** 对于处理数组的递归函数，终止条件可以是数组长度为 0。
- **树的深度：** 对于处理树的递归函数，终止条件可以是树的深度达到某个阈值。
- **数值范围：** 对于处理数值的递归函数，终止条件可以是数值达到某个边界值。

### 2.2 递归算法的性能分析

#### 2.2.1 时间复杂度和空间复杂度

递归算法的性能分析主要关注时间复杂度和空间复杂度。

- **时间复杂度：** 递归算法的时间复杂度取决于递归调用的次数和每次调用的时间开销。
- **空间复杂度：** 递归算法的空间复杂度取决于递归调用的深度和每次调用所需的空间。

#### 2.2.2 递归深度和栈空间

递归调用的深度会影响栈空间的消耗。栈空间是计算机内存中用于存储函数调用信息和局部变量的区域。递归调用过多会导致栈空间溢出，从而引发运行时错误。

例如，以下递归函数计算阶乘：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)

该函数的递归深度为 `n`，空间复杂度为 `O(n)`。如果 `n` 较大，则可能会导致栈空间溢出。

# 3. 递归算法的实践应用

### 3.1 分治算法

#### 3.1.1 分治算法的原理和步骤

分治算法是一种将问题分解为较小规模的子问题，再分别解决子问题，最后合并子问题的解来得到原问题的解的算法。其基本步骤如下：

1. **分解：**将原问题分解为几个规模较小的子问题。
2. **求解：**递归地求解每个子问题。
3. **合并：**将子问题的解合并起来，得到原问题的解。

#### 3.1.2 分治算法的经典应用

分治算法有许多经典应用，例如：

- **归并排序：**将数组分解为两个子数组，递归地排序子数组，再合并两个有序子数组。
- **快速排序：**选择一个基准元素，将数组划分为两个子数组，递归地排序子数组，再合并两个有序子数组。
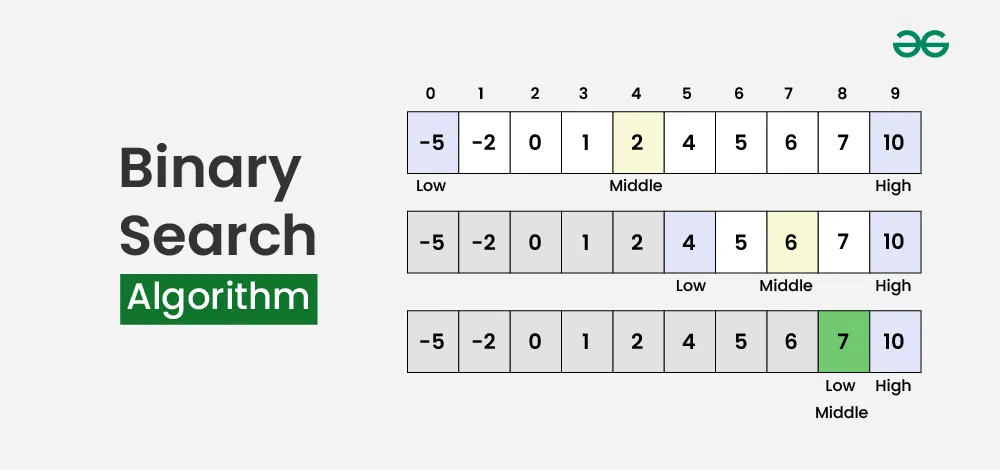
- **二分查找：**将有序数组分解为两个子数组，递归地在子数组中查找目标元素，直到找到或确定目标元素不存在。

### 3.2 回溯算法

#### 3.2.1 回溯算法的原理和步骤

回溯算法是一种通过尝试所有可能的解来解决问题的算法。其基本步骤如下：

1. **尝试：**从当前状态出发，尝试一个可能的解。
2. **递归：**如果尝试的解是可行的，则递归地探索该解的子问题。
3. **回溯：**如果尝试的解不可行，则回溯到上一个状态，尝试另一个可能的解。

#### 3.2.2 回溯算法的经典应用

回溯算法有许多经典应用，例如：

- **走迷宫：**从迷宫的入口开始，尝试所有可能的路径，直到找到出口或确定迷宫无解。
- **八皇后问题：**在8x8棋盘上放置8个皇后，使得它们互不攻击。
- **旅行商问题：**给定一组城市和两城市之间的距离，找到一条访问所有城市并返回起点的最短路径。

### 3.3 动态规划算法

#### 3.3.1 动态规划算法的原理和步骤

动态规划算法是一种通过将问题分解为重叠子问题，并保存子问题的解来解决问题的算法。其基本步骤如下：

1. **分解：**将原问题分解为若干个重叠子问题。
2. **存储：**保存子问题的解，以避免重复计算。
3. **求解：**从最小的子问题开始，递归地求解子问题，并利用存储的子问题的解来求解更大的子问题