PID控制器在不同行业的应用大全：探索工业自动化控制的广阔天地，助你拓展业务版图

# 1. PID控制器的基础理论**

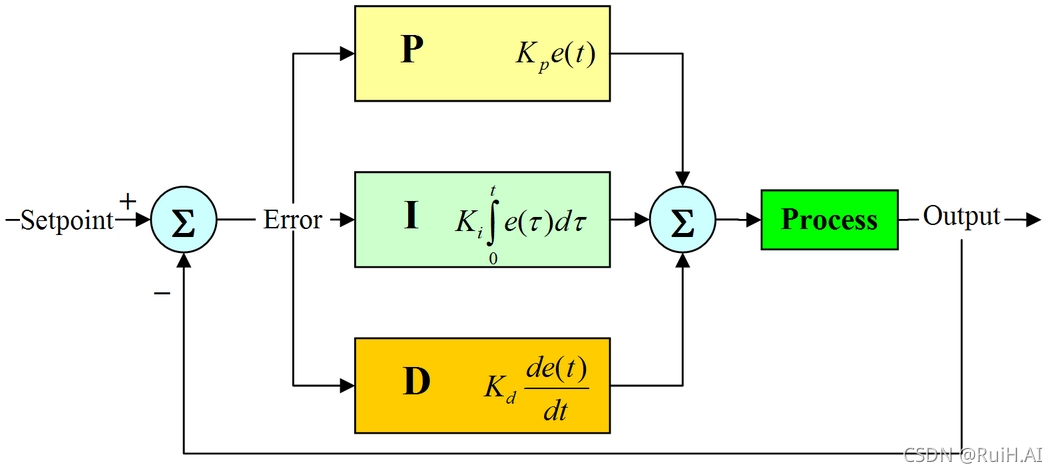
PID控制器是一种广泛应用于工业自动化领域的反馈控制系统。其基本原理是通过测量被控对象的输出值与期望值之间的偏差，并根据偏差的大小和变化率来调整控制器的输出，从而使被控对象的输出值尽可能接近期望值。

PID控制器由三个基本参数组成：比例参数（P）、积分参数（I）和微分参数（D）。比例参数决定了控制器的输出与偏差成正比的大小，积分参数决定了控制器输出与偏差积分成正比的大小，微分参数决定了控制器输出与偏差变化率成正比的大小。通过调整这三个参数，可以使控制器具有不同的控制特性，以适应不同的被控对象。

# 2.1 PID控制器参数的整定方法

### 2.1.1 Ziegler-Nichols方法

Ziegler-Nichols方法是一种经典的PID控制器参数整定方法，适用于具有单时间常数的系统。该方法基于系统阶跃响应的特性，通过测量系统对阶跃输入的响应，可以快速确定PID控制器的比例增益（Kp）、积分时间（Ti）和微分时间（Td）。

**步骤：**

1. 将系统置于开环状态，即断开控制器与执行器的连接。
2. 向系统施加一个阶跃输入。
3. 记录系统输出的响应曲线。
4. 测量响应曲线的以下参数：
- 延迟时间（td）：输出开始响应的时间。
- 上升时间（tr）：输出达到稳态值的63.2%所需的时间。
- 峰值时间（tp）：输出达到峰值的时间。
- 超调量（Mp）：输出峰值与稳态值的差值，以稳态值为基准。

**参数计算公式：**

| 参数 | 公式 |
|---|---|
| Kp | 0.6 * Kcu |
| Ti | 2 * P |
| Td | 0.5 * P |

其中：

- Kcu：临界增益，即系统在开环状态下出现持续振荡时的增益。
- P：系统的时间常数，可通过tr或tp计算得到。

**代码示例：**

import numpy as np
import matplotlib.pyplot as plt

# 系统阶跃响应
def step_response(t, K, tau):
    y = K * (1 - np.exp(-t / tau))
    return y

# Ziegler-Nichols参数整定
def ziegler_nichols(t, y):
    # 测量响应参数
    td = t[np.argmax(y)]
    tr = t[np.where(y >= 0.632 * y[-1])[0][0]]
    tp = t[np.argmax(y)]
    Mp = (np.max(y) - y[-1]) / y[-1]

    # 计算参数
    Kcu = K / Mp
    P = tr / np.log(1 - Mp)
    Kp = 0.6 * Kcu
    Ti = 2 * P
    Td = 0.5 * P

    return Kp, Ti, Td

# 测试
t = np.linspace(0, 10, 100)
K = 1
tau = 1
y = step_response(t, K, tau)
Kp, Ti, Td = ziegler_nichols(t, y)

# 输出参数
print("Kp:", Kp)
print("Ti:", Ti)
print("Td:", Td)

# 绘制响应曲线
plt.plot(t, y)
plt.xlabel("Time (s)")
plt.ylabel("Output")
plt.show()

### 2.1.2 Cohen-Coon方法

Cohen-Coon方法是一种基于系统传递函数的PID控制器参数整定方法。该方法适用于具有任意阶数的系统，但需要知道系统的传递函数。

**步骤：**

1. 获得系统的传递函数。
2. 根据传递函数的极点和零点，计算以下参数：
- 惯性时间（τ）：极点绝对值的倒数。
- 时延时间（θ）：零点绝对值的倒数。
- 稳态增益（K）：传递函数在零频率处的增益。

**参数计算公式：**

| 参数 | 公式 |
|---|---|
| Kp | Kc * (0.33 * τ + 0.5 * θ) |
| Ti | 2 * τ |
| Td | 0.5 * τ |

其中：

- Kc：临界增益，可通过传递函数的幅值频率响应曲线确定。

**代码示例：**

import sympy
import numpy as np
import matplotlib.pyplot as plt

# 系统传递函数
s = sympy.Symbol("s")
G = K / (s * (s + 1) * (s + 2))

# Cohen-Coon参数整定
tau = 1
theta = 0
Kc = 1
Kp = Kc * (0.33 * tau + 0.5 * theta)
Ti = 2 * tau
Td = 0.5 * tau

# 输出参数
print("Kp:", Kp)
print("Ti:", Ti)
print("Td:", Td)

# 绘制幅值频率响应曲线
w = np.logspace(-2, 2, 100)
mag, phase = sympy.freqresp(G, w)
plt.loglog(w, mag)
plt.xlabel("Frequency (rad/s)")
plt.ylabel("Magnitude (dB)")
plt.show()

### 2.1.3 IMC方法

IMC（Internal Model Control）方法是一种基于模型的PID控制器参数整定方法。该方法需要建立系统的数学模型，并将其作为控制器内部模型。

**步骤：**

1. 建立系统的数学模型。
2. 将模型与控制器内部模型进行匹配。
3. 根据模型参数，计算PID控制器的参数。

**参数计算公式：**

| 参数 | 公式 |
|---|---|
| Kp | K * (1 + τ / Ti) |
| Ti | τ / (2 * ζ) |
| Td | τ / (4 * ζ) |

其中：

- K：模型的稳态增益。
- τ：模型的时间常数。
- ζ：模型的阻尼比。

**代码示例：**

import numpy as np
import sympy
import matplotlib.pyplot as plt

# 系统模型
s = sympy.Symbol("s")
G = K / (s * (s + 1) * (s + 2))

# IMC参数整定
tau = 1
zeta = 0.5
K = 1
Kp = K * (1 + tau / Ti)
Ti = tau / (2 * zeta)
Td = tau / (4 * zeta)

# 输出参数
print("Kp:", Kp)
print("Ti:", Ti)
print("Td:", Td)

# 绘制系统响应
t = np.linspace(0, 10, 100)
y = sympy.impulse_response(G, t)
plt.plot(t, y)
plt.xlabel("Time (s)")
plt.ylabel("Output")
plt.show()

# 3. PID控制器的进阶应用**

### 3.1 PID控制器的非线性补偿方法

#### 3.1.1 反馈线性化

**原理：**

反馈线性化是一种非线性控制方法，通过引入非线性反馈来将非线性系统线性化。具体来说，它通过构造一个非线性反馈器，将非线性系统变换为一个线性系统，从而可以使用线性的PID控制器进行控制。

**实现：**

import numpy as np

def feedback_linearization(plant, u_nl):
    """
    反馈线性化函数

    参数：
        plant: 非线性系统模型
        u_nl: 非线性控制输入

    返回：
        u_lin: 线性控制输入
    """

    # 计算非线性反馈器
    f_nl = plant.f(x, u_nl)
    g_nl = plant.g(x, u_nl)
    h_nl = plant.h(x, u_nl)

    # 构造线性控制输入
    u_lin = np.linalg.inv(g_nl) * (u_nl - f_nl - h_nl * x)

    return u_lin

**代码逻辑分析：**

* `plant.f(