PID控制器参数整定秘籍：探索优化控制性能的奥秘，让你的系统运行更顺畅

# 1. PID控制理论基础

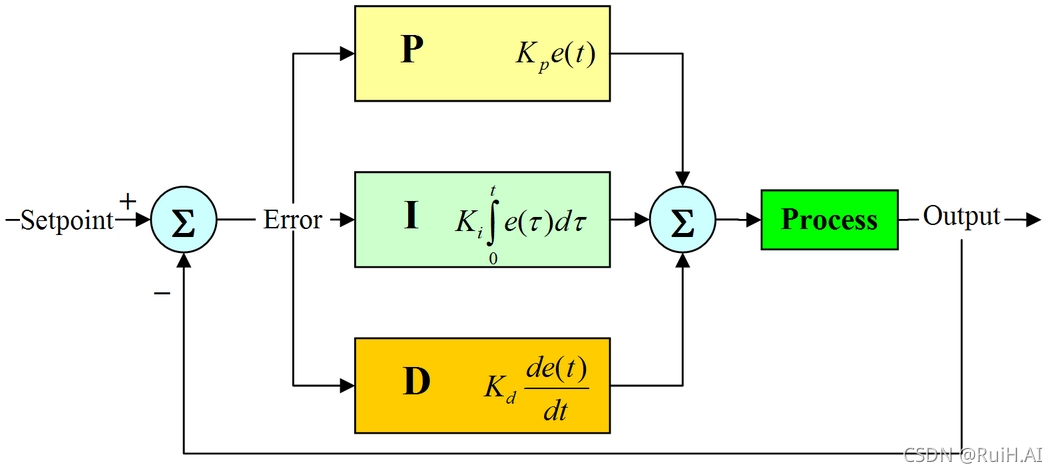
PID（比例-积分-微分）控制是一种广泛应用于工业控制领域的反馈控制算法。其基本原理是通过测量被控变量与设定值之间的偏差，并根据偏差的大小和变化率，计算出适当的控制量，以使被控变量尽可能接近设定值。

PID控制算法的数学表达式为：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

- `u(t)` 为控制量
- `e(t)` 为偏差，即设定值与被控变量之差
- `Kp` 为比例增益
- `Ki` 为积分增益
- `Kd` 为微分增益

# 2. PID控制器参数整定方法

### 2.1 Ziegler-Nichols方法

Ziegler-Nichols方法是一种经典的PID参数整定方法，它基于系统的阶跃响应或频率响应特性来确定PID控制器的参数。

#### 2.1.1 阶跃响应法

**原理：**

1. 向系统施加一个阶跃输入。
2. 记录系统的输出响应。
3. 根据输出响应的特性确定PID参数。

**步骤：**

1. 将PID控制器设置为纯比例控制（I=0，D=0）。
2. 逐渐增加比例增益（Kp）直到系统出现持续振荡。
3. 记录振荡的周期（Tu）和振幅（Au）。
4. 根据Tu和Au计算PID参数：
- Kp = 0.45 * (Tu / Au)
- Ti = 0.85 * Tu
- Td = 0.12 * Tu

**代码块：**

import control

# 定义系统传递函数
G = control.TransferFunction([1], [1, 2, 1])

# 施加阶跃输入
t = np.linspace(0, 10, 100)
u = np.zeros(len(t))
u[0] = 1

# 模拟系统响应
y, t, x = control.forced_response(G, u, t)

# 计算Tu和Au
Tu = np.max(t[np.where(y > 0.5)[0]]) - np.min(t[np.where(y > 0.5)[0]])
Au = np.max(y) - np.min(y)

# 计算PID参数
Kp = 0.45 * (Tu / Au)
Ti = 0.85 * Tu
Td = 0.12 * Tu

print("PID参数：")
print("Kp =", Kp)
print("Ti =", Ti)
print("Td =", Td)

**逻辑分析：**

* `forced_response()`函数模拟了系统对阶跃输入的响应。
* `np.where(y > 0.5)[0]`返回了输出信号y大于0.5的索引。
* `np.max()`和`np.min()`函数分别计算了振荡的周期和振幅。
* 根据Ziegler-Nichols公式计算了PID参数。

#### 2.1.2 频率响应法

**原理：**

1. 向系统施加一个正弦输入。
2. 记录系统的幅频响应。
3. 根据幅频响应的特性确定PID参数。

**步骤：**

1. 将PID控制器设置为纯比例控制（I=0，D=0）。
2. 逐渐增加比例增益（Kp）直到系统出现-3dB的幅值衰减。
3. 记录此时对应的频率（ωc）。
4. 根据ωc计算PID参数：
- Kp = 0.6 * Kc
- Ti = 2 * π / ωc
- Td = 0.5 * Ti

**代码块：**

import control

# 定义系统传递函数
G = control.TransferFunction([1], [1, 2, 1])

# 施加正弦输入
t = np.linspace(0, 10, 100)
u = np.sin(2 * np.pi * 0.5 * t)

# 模拟系统响应
y, t, x = control.forced_response(G, u, t)

# 计算幅频响应
mag, phase, omega = control.bode_plot(G, w=np.logspace(-1, 2, 100))

# 计算-3dB频率
omega_c = omega[np.where(mag < -3)[0][0]]

# 计算PID参数
Kp = 0.6 * Kc
Ti = 2 * np.pi / omega_c
Td = 0.5 * Ti

print("PID参数：")
print("Kp =", Kp)
print("Ti =", Ti)
print("Td =", Td)

**逻辑分析：**

* `bode_plot()`函数计算了系统的幅频响应。
* `np.where(mag < -3)[0][0]`返回了幅值衰减-3dB的频率索引。
* 根据Ziegler-Nichols公式计算了PID参数。

# 3.1 实验数据采集

#### 3.1.1 过程变量测量

过程变量测量是参数优化实践中的关键步骤。它涉及测量和记录受控变量（PV）随时间变化的值。PV是需要控制的系统输出，例如温度、压力或流量。

**测量方法：**

* **传感器：**使用温度传感器、压力传感器或流量计等传感器直接测量PV。
* **数据采集系统：**使用数据采集系统（DAQ）或可编程逻辑控制器（PLC）记录传感器输出。

#### 3.1.2 控制变量调整

控制变量（MV）是用来控制PV的输入变量，例如加热器功率、阀门开度或泵速。在实验数据采集期间，需要调整MV以激发系统响应并收集PV数据。

**调整方法：**

* **阶跃响应：**突然改变MV，观察PV的响应。
* **正弦波响应：**以正弦波形式改变MV，分析PV的频率响应。
* **随机扰动：**随机改变MV，观察PV的动态行为。

### 3.2 参数整定工具

#### 3.2.1 MATLAB PID工具箱

MATLAB PID工具箱是一个功能强大的工具，用于PID控制器的设计、仿真和分析。它提供了各种方法来整定PID参数，包括：

* **Ziegler-Nichols方法：**使用阶跃响应或频率响应数据自动计算PID参数。
* **Cohen-Coon方法：**根据过程反应曲线或时间常数估计PID参数。
* **IMC方法：**基于内部模型控制原理计算PID参数。

#### 3.2.2 Simulink PID模块

Simulink PID模块是一个Simulink库，用于设计和仿真PID控制器。它提供了可配置的PID参数，允许用户调整参数并观察其对系统响应的影响。

### 3.3 参数优化算法

#### 3.3.1 粒子群优化

粒子群优化（PSO）是一种基于群体的优化算法，灵感来自鸟群或鱼群的行为。它通过迭代更新粒子位置来搜索最优解。

**算法流程：**

1. 初始化粒子群，每个粒子代表一组PID参数。
2. 计算每个粒子的适应度函数，该函数衡量PID参数的性能。
3. 更新每个粒子的速度和位置，基于当前位置、最佳位置和全局最佳位置。
4. 重复步骤2-3，直到达到停止条件。

#### 3.3.2 遗传算法

遗传算法（GA）是一种基于进化的优化算法，模拟生物进化过程。它通过选择、交叉和突变操作来搜索最优解。

**算法流程：**

1. 初始化种群，每个个体代表一组PID参数。
2. 计算每个个体的适应度函数。
3. 选择适应度较高的个体进行交叉和突变。
4. 生成新的种群，包含交叉和突变后的个体。
5. 重复步骤2-4，直到达到停止条件。

# 4. PID控制器高级应用

### 4.1 自整定PID控制器

#### 4.1.1 自适应控制原理

自适应控制是一种能够自动调整自身参数以适应系统变化的控制方法。自整定PID控制器是一种自适应控制算法，它能够根据被控对象的特性自动调整PID参数，从而实现更好的控制效果。

自适应控制原理主要基于以下几个方面：

- **参数识别：**通过在线测量被控对象的响应，识别出其参数的变化。
- **参数调整：**根据参数识别结果，调整PID参数以匹配被控对象的变化。
- **稳定性分析：**实时监控控制系统的稳定性，并根据需要调整参数以确保稳定性。

#### 4.1.2 自整定算法

常用的自整定算法包括：

- **基于模型的自整定算法：**建立被控对象的数学模型，并根据模型参数的变化调整PID参数。
- **基于增益调度算法：**根据被控对象的工作条件（如温度、压力等）调整PID参数。
- **基于模糊逻辑算法：**利用模糊逻辑规则库来调整PID参数，实现自整定。

### 4.2 模糊PID控制器

#### 4.2.1 模糊逻辑控制简介

模糊逻辑控制是一种基于模糊集合论的控制方法。它将被控对象的输入和输出变量划分为模糊集合，并利用模糊规则库来进行控制。

模糊集合是一种不精确的集合，其元素具有隶属度。隶属度表示元素属于该集合的程度，取值范围为[0, 1]。

模糊规则库是一组模糊规则，每个规则由一个条件部分和一个动作部分组成。条件部分描述了输入变量的模糊集合，动作部分描述了输出变量的模糊集合。

#### 4.2.2 模糊PID控制器设计

模糊PID控制器将传统PID控制器的比例、积分和微分项替换为模糊逻辑控制模块。

**比例模块：**将误差和误差变化率划分为模糊集合，并根据模糊规则库计算比例增益。

**积分模块：**将误差的积分划分为模糊集合，并根据模糊规则库计算积分时间。

**微分模块：**将误差变化率划分为模糊集合，并根据模糊规则库计算微分时间。

模糊PID控制器通过综合三个模块的输出，得到最终的控制输出。

### 4.3 神经网络PID控制器

#### 4.3.1 神经网络的基本原理

神经网络是一种受生物神经系统启发的机器学习模型。它由相互连接的神经元组成，每个神经元具有一个权重和一个激活函数。

神经网络通过训练数据学习输入和输出之间的关系。训练过程中，神经网络不断调整权重，以最小化训练数据的误差。

#### 4.3.2 神经网络PID控制器实现

神经网络PID控制器将神经网络用于PID参数的调整。

**神经网络结构：**神经网络通常采用多层感知器（MLP）结构，输入层为误差和误差变化率，输出层为PID参数。

**训练算法：**神经网络使用反向传播算法进行训练，训练数据为被控对象的输入和输出数据。

**参数调整：**训练后的神经网络可以根据新的输入数据实时调整PID参数，从而实现自整定。

# 5. PID控制器在工业领域的应用实例

### 5.1 温度控制系统

#### 5.1.1 PID控制器在温度控制中的作用

PID控制器在温度控制系统中发挥着至关重要的作用。它通过测量温度传感器获取的实际温度，与设定温度进行比较，计算出偏差，并根据偏差调整控制变量（如加热器功率或冷却器流量），以使实际温度接近设定温度。

#### 5.1.2 温度控制系统的优化

为了优化温度控制系统的性能，可以采用以下方法：

- **参数整定：**根据温度控制系统的动态特性，合理整定PID控制器的参数（比例、积分、微分），以获得最佳的控制效果。
- **自整定：**采用自整定算法，使PID控制器能够在线调整参数，适应系统参数变化或外部干扰。
- **模糊控制：**利用模糊逻辑处理温度控制系统的非线性、不确定性，设计模糊PID控制器，提高控制精度和鲁棒性。
- **神经网络控制：**利用神经网络的学习和泛化能力，设计神经网络PID控制器，实现温度控制系统的自适应和智能化。

### 5.2 液位控制系统

#### 5.2.1 PID控制器在液位控制中的应用

PID控制器在液位控制系统中同样扮演着重要的角色。它通过测量液位传感器获取的液位值，与设定液位进行比较，计算出偏差，并调整控制变量（如泵流量或阀门开度），以使液位保持在设定值附近。

#### 5.2.2 液位控制系统的稳定性分析

液位控制系统是一个典型的反馈控制系统。为了保证系统的稳定性，需要对系统进行稳定性分析。常用的方法有：

- **根轨迹法：**绘制PID控制器的根轨迹图，分析系统极点的分布，判断系统的稳定性。
- **奈奎斯特稳定性判据：**绘制PID控制器的开环传递函数的奈奎斯特图，判断系统是否存在闭环稳定。
- **波德图法：**绘制PID控制器的开环传递函数的波德图，分析系统的相位裕度和增益裕度，判断系统的稳定性。