PID控制器在信号处理中的妙用：探索其在信号分析中的作用，助你实现精准信号处理

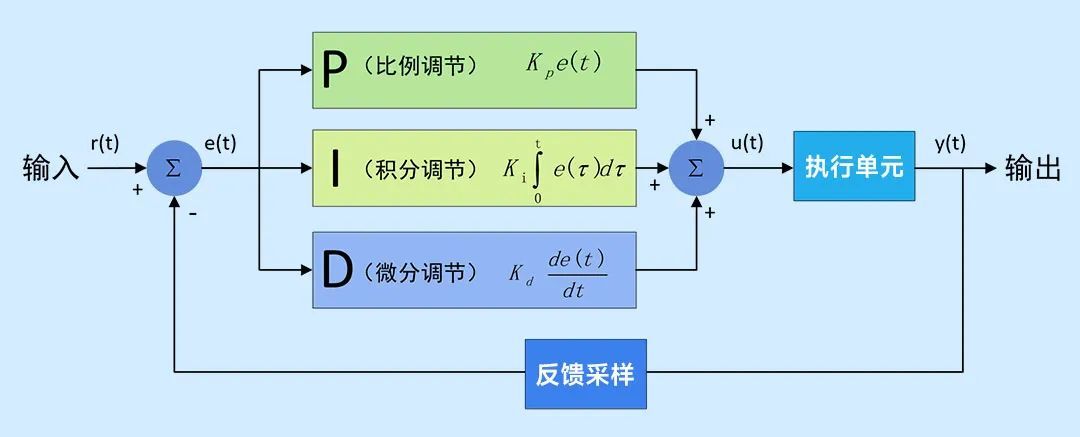
# 1. PID控制器的基本原理**

PID控制器（比例-积分-微分控制器）是一种经典的反馈控制系统，广泛应用于各种工业和科学领域。其基本原理是通过测量系统的输出与期望值之间的误差，并根据误差的比例、积分和微分值来调整控制输出，从而使系统输出接近期望值。

PID控制器的数学模型如下：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* u(t) 为控制输出
* e(t) 为误差（期望值 - 输出值）
* Kp 为比例增益
* Ki 为积分增益
* Kd 为微分增益

# 2. PID控制器在信号分析中的应用

### 2.1 信号处理中的PID控制器设计

#### 2.1.1 PID控制器的参数调整

PID控制器参数的调整是至关重要的，它直接影响控制器的性能和稳定性。常用的参数调整方法包括：

- **齐格勒-尼科尔斯法：**一种基于系统阶跃响应的经验法则，可快速估计PID控制器的参数。
- **极限循环法：**通过逐渐增大控制器增益，直到系统出现极限循环，然后根据极限循环的周期和幅度计算控制器参数。
- **自适应调整：**使用算法在线调整控制器参数，以适应系统变化或扰动。

#### 2.1.2 PID控制器的稳定性分析

PID控制器的稳定性是保证系统正常运行的关键。常用的稳定性分析方法包括：

- **根轨迹法：**通过绘制系统闭环传递函数的根轨迹，分析系统稳定性。
- **奈奎斯特稳定性判据：**通过绘制系统开环传递函数的奈奎斯特曲线，判断系统稳定性。
- **波德图：**通过绘制系统开环传递函数的波德图，分析系统稳定性和相位裕度。

### 2.2 PID控制器在信号滤波中的应用

#### 2.2.1 PID控制器作为低通滤波器

PID控制器可以作为低通滤波器，滤除信号中的高频噪声。其原理是通过调整控制器参数，使系统对低频信号有较大的增益，而对高频信号有较小的增益。

import numpy as np
import matplotlib.pyplot as plt

# 生成原始信号
t = np.linspace(0, 1, 1000)
signal = np.sin(2 * np.pi * 10 * t) + np.random.randn(1000) * 0.1

# 设计PID控制器作为低通滤波器
Kp = 0.1
Ki = 0.01
Kd = 0.001
pid = PID(Kp, Ki, Kd)

# 滤波信号
filtered_signal = pid.filter(signal)

# 绘制原始信号和滤波信号
plt.plot(t, signal, label='Original signal')
plt.plot(t, filtered_signal, label='Filtered signal')
plt.legend()
plt.show()

**逻辑分析：**

* `Kp`、`Ki`、`Kd`分别为PID控制器的比例、积分、微分增益。
* `pid.filter(signal)`使用PID控制器对信号进行滤波。
* 绘制原始信号和滤波信号，观察滤