PID控制器在数据分析中的应用：揭示其在机器学习中的作用，助你提升数据分析能力

# 1. PID控制器基础理论

PID控制器是一种广泛应用于工业控制领域的经典控制算法，它具有结构简单、易于实现、鲁棒性强等优点。在数据分析领域，PID控制器也得到了广泛的应用，可以有效地解决时序数据预测、图像处理等问题。

### 1.1 PID控制器的原理

PID控制器是一种反馈控制算法，其基本原理是根据系统的误差信号（即期望值与实际值之差）来调整控制输出，从而使系统输出接近期望值。PID控制器由比例、积分和微分三个部分组成，分别对应于误差信号的当前值、过去值和未来值。

### 1.2 PID控制器的数学模型

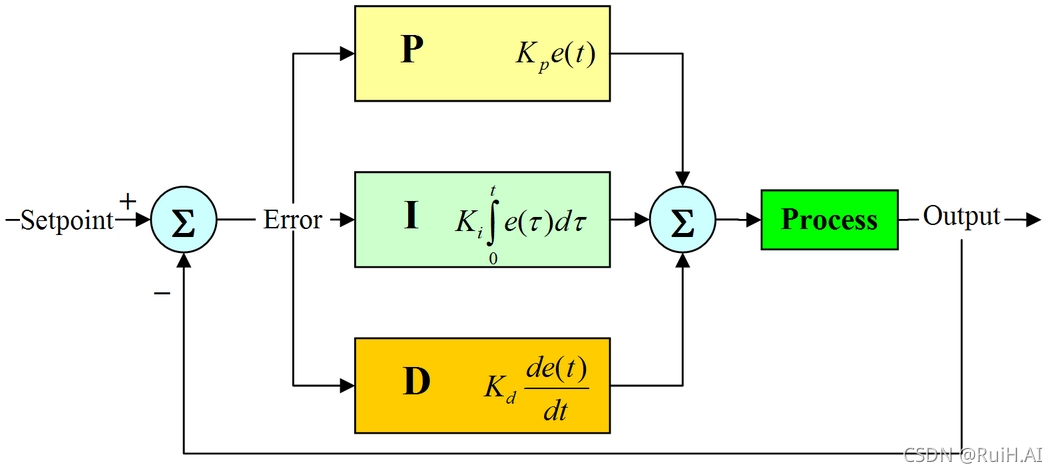
PID控制器的数学模型如下：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `u(t)` 为控制输出
* `e(t)` 为误差信号
* `Kp` 为比例增益
* `Ki` 为积分增益
* `Kd` 为微分增益

# 2. PID控制器在数据分析中的应用

### 2.1 PID控制器的原理和数学模型

#### 2.1.1 比例、积分、微分作用

PID控制器是一种反馈控制系统，它通过测量被控对象的输出，并将其与期望值进行比较，来计算出控制信号。控制信号的大小和方向将影响被控对象的输出，从而实现对被控对象的控制。

PID控制器由三个基本组成部分组成：比例（P）、积分（I）和微分（D）。

* **比例作用**：比例作用根据被控对象输出与期望值之间的误差，产生一个与误差成正比的控制信号。误差越大，控制信号越大。
* **积分作用**：积分作用根据误差随时间的累积值，产生一个与误差积分成正比的控制信号。误差累积的时间越长，控制信号越大。
* **微分作用**：微分作用根据误差变化率，产生一个与误差变化率成正比的控制信号。误差变化率越大，控制信号越大。

#### 2.1.2 PID控制器的参数整定

PID控制器的参数整定是指确定比例、积分和微分三个参数的值，以使控制器能够有效地控制被控对象。参数整定是一个复杂的过程，需要考虑被控对象的特性、控制目标和系统稳定性等因素。

常用的参数整定方法包括：

* **齐格勒-尼科尔斯法**：一种基于被控对象阶跃响应的经验法。
* **柯恩-科恩法**：一种基于被控对象频率响应的经验法。
* **模型预测控制（MPC）**：一种基于数学模型的优化方法。

### 2.2 PID控制器在机器学习中的作用

#### 2.2.1 优化机器学习模型的参数

PID控制器可以用于优化机器学习模型的参数。通过将机器学习模型的输出作为被控对象，并使用PID控制器来调整模型的参数，可以使模型的性能达到最优。

例如，在神经网络模型中，PID控制器可以用来调整网络的权重和偏置，以最小化模型的损失函数。

#### 2.2.2 提高机器学习模型的鲁棒性

PID控制器还可以用于提高机器学习模型的鲁棒性。通过将PID控制器与机器学习模型结合使用，可以使模型对噪声和干扰更加鲁棒。

例如，在图像识别模型中，PID控制器可以用来调整模型的滤波器参数，以减少噪声对模型的影响。

**代码示例：**

import numpy as np
import matplotlib.pyplot as plt

# 定义被控对象
class Plant:
    def __init__(self, a, b):
        self.a = a
        self.b = b

    def update(self, u):
        self.x = self.a * self.x + self.b * u

# 定义PID控制器
class PIDController:
    def __init__(self, Kp, Ki, Kd):
        self.Kp = Kp
        self.Ki = Ki
        self.Kd = Kd
        self.err