【二叉树操作技巧】：JavaScript中实现与技巧大揭秘

# 1. 二叉树基础概念与特性

## 1.1 二叉树定义

在计算机科学中，**二叉树**是一种特殊的数据结构，其中每个节点最多有两个子节点，通常被称为**左子节点**和**右子节点**。这种结构类似于一个倒置的家族树，其中根节点代表祖先，而子节点代表后代。二叉树是许多高级数据结构和算法的基础，如二叉搜索树、堆和AVL树。

## 1.2 二叉树的类型

二叉树根据其结构的不同，可以分为多种类型：
- **完全二叉树**：除了最后一层外，每一层都被完全填满，且所有节点都尽可能地向左。
- **满二叉树**：每一层的所有节点都有两个子节点，不存在只拥有一个子节点的节点。
- **平衡二叉树**（如AVL树）：任何两个叶子节点之间的高度差都不超过1，保证了操作的高效性。
- **二叉搜索树**（BST）：对于树中的每个节点，其左子树中所有元素的值均小于该节点值，右子树中所有元素的值均大于该节点值。

## 1.3 二叉树的重要性

二叉树之所以在计算机科学中被广泛应用，主要得益于其高效的数据检索、插入和删除操作。通过特定的遍历方法，如前序、中序和后序遍历，我们可以访问树中的所有节点，并按特定顺序处理数据。二叉树的这些操作为其他复杂数据结构的实现提供了基础，如排序算法和索引结构。

graph TD
    root(根节点) --> left(左子树)
    root --> right(右子树)
    left --> leftChild(左子节点)
    left --> leftRight(左右子节点)
    right --> rightChild(右子节点)
    right --> rightLeft(右左子节点)

在下一章，我们将深入探讨二叉树的递归操作，了解其如何通过递归算法来简化复杂的树结构处理。

# 2. 二叉树的递归操作详解

### 2.1 递归算法理论基础

#### 2.1.1 递归的定义和工作原理

递归是一种在解决问题时，将问题分解为更小的、相似的子问题，直到这些子问题简单到可以直接解决。然后将这些子问题的解合并以构造原问题的解的算法设计策略。在计算机科学中，递归方法允许程序通过调用自身来解决问题。

递归方法通常包含两个主要部分：基本情况（base case）和递归步骤（recursive step）。基本情况是递归调用链中的终止条件，通常是问题的最简单实例，可以直接解决而无需进一步分解。递归步骤则将原问题分解为更小的问题，并且调用自身来解决这些问题。

递归算法的工作原理依赖于栈数据结构，每一次函数调用都会将一个新的函数环境压入栈中，当达到基本情况时，函数开始返回，并且逐层释放栈中的函数环境，最终得到最终解。

#### 2.1.2 递归与分治策略

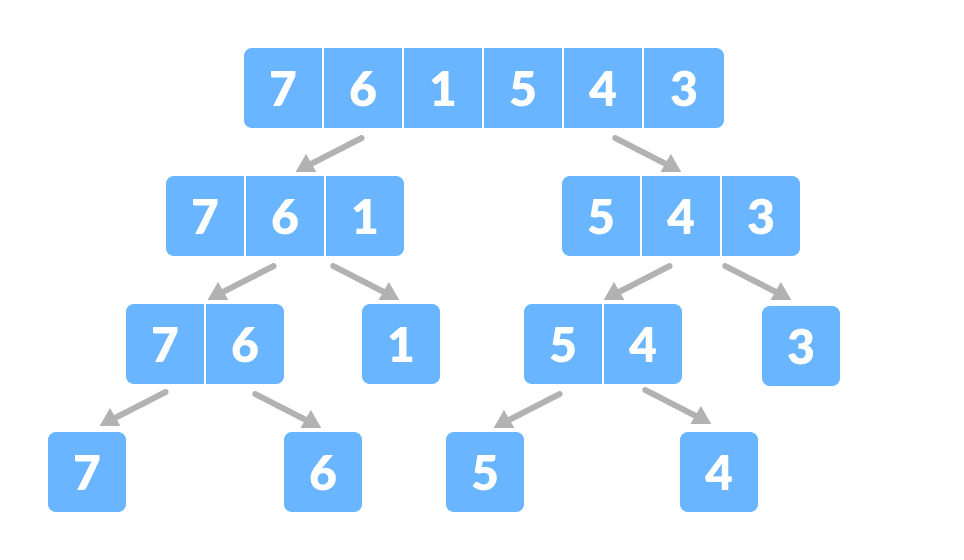
分治策略是一种递归策略，它将原问题分解为若干个规模较小但类似于原问题的子问题，递归地解决这些子问题，然后再合并这些子问题的解以得到原问题的解。

在二叉树的递归操作中，分治策略特别有用。例如，在二叉树的遍历操作中，可以通过递归地遍历左子树和右子树，然后处理根节点来完成前序、中序或后序遍历。

分治策略的基本思想可以概括为三个步骤：

1. 分解：将原问题分解成一系列子问题。
2. 解决：递归地解决各个子问题。如果子问题足够小，则直接求解。
3. 合并：将各个子问题的解合并成原问题的解。

### 2.2 二叉树的遍历方法

#### 2.2.1 前序遍历算法实现

前序遍历是一种深度优先遍历方法，按照“根-左-右”的顺序访问二叉树的每个节点。在递归实现中，我们首先访问根节点，然后递归地访问左子树，最后递归地访问右子树。

以下是前序遍历的递归算法实现：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def preorderTraversal(root):
    if not root:
        return []
    result = [root.val]  # 访问根节点
    result += preorderTraversal(root.left)  # 递归访问左子树
    result += preorderTraversal(root.right)  # 递归访问右子树
    return result

# 示例：构建二叉树并遍历
# 构建如下结构的二叉树:
#     1
#    / \
#   2   3
#  / \
# 4   5
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print(preorderTraversal(root))  # 输出: [1, 2, 4, 5, 3]

在上述代码中，`preorderTraversal` 函数首先检查当前节点是否存在，如果不存在，返回空列表。如果存在，则将节点值添加到结果列表中，然后递归调用自身来遍历左子树和右子树。

#### 2.2.2 中序遍历算法实现

中序遍历是另一种深度优先遍历方法，按照“左-根-右”的顺序访问二叉树的每个节点。在递归实现中，我们首先递归地访问左子树，然后访问根节点，最后递归地访问右子树。

以下是中序遍历的递归算法实现：

def inorderTraversal(root):
    if not root:
        return []
    result = inorderTraversal(root.left)  # 递归访问左子树
    result += [root.val]  # 访问根节点
    result += inorderTraversal(root.right)  # 递归访问右子树
    return result

print(inorderTraversal(root))  # 输出: [4, 2, 5, 1, 3]

#### 2.2.3 后序遍历算法实现

后序遍历是深度优先遍历方法的另一种形式，按照“左-右-根”的顺序访问二叉树的每个节点。在递归实现中，我们首先递归地访问左子树，然后递归地访问右子树，最后访问根节点。

以下是后序遍历的递归算法实现：

def postorderTraversal(root):
    if not root:
        return []
    result = postorderTraversal(root.left)  # 递归访问左子树
    result += postorderTraversal(root.right)  # 递归访问右子树
    result += [root.val]  # 访问根节点
    return result

print(postorderTraversal(root))  # 输出: [4, 5, 2, 3, 1]

通过这三个基本的递归遍历算法，我们可以对二叉树的所有节点进行访问，并根据需要进行相应的处理。这些操作是进一步二叉树处理和操作的基础。

# 3. 二叉树的非递归操作与技巧

## 3.1 非递归操作理论基础

### 3.1.1 栈与队列在树遍历中的应用

在树的遍历算法中，递归方法非常直观且易于实现，但在某些情况下，递归方法可能会导致堆栈溢出，特别是在处理具有非常深的树结构时。为了克服这些问题，可以使用栈和队列的数据结构来实现非递归遍历。

栈在树的遍历中主要用于实现深度优先搜索（DFS），特别是在前序和后序遍历中。在DFS中，我们通常先访问根节点，然后将根节点的子节点压入栈中，再依次从栈中弹出节点进行访问。这种方式可以保证我们按照节点的“深度”优先进行访问。

队列则在实现广度优先搜索（BFS）时发挥关键作用。在BFS中，我们按照从根节点开始，逐层访问树的节点。具体操作是，首先将根节点入队，然后在队列不为空的情况下，依次出队节点，并将其子节点入队。通过这种方式，我们可以逐层地访问整棵树。

以下是使用Python代码实现非递归前序遍历的示例：

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.val = value
        self.left = left
        self.right = right

def preorderTraversal(root):
    if not root:
        return []
    stack, result = [root], []
    while stack:
        node = stack.pop()
        result.append(node.val)
        # 注意，右子节点先入栈，保证左子节点后出栈
        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)
    return result

### 3.1.2 迭代算法的设计思路

迭代算法是通过显式地使用数据结构（如栈或队列）来控制算法执行流程的一种方法。与递归算法相比，迭代算法通常在空间使用上更为高效，因为它们避免了递