【FFT算法在量子计算中的角色】：量子位频谱分析的桥梁，深入研究


# 摘要
本文综合探讨了量子计算与频率分析的交汇点，首先介绍了量子计算与频率分析的基础知识，然后详细概述了快速傅里叶变换(FFT)算法，并探讨了量子位在量子频谱分析中的应用。文章重点分析了FFT算法在量子计算领域的应用实践，旨在说明量子算法如何改善传统频谱分析的性能。此外，本文还对量子FFT算法的理论框架进行了深入的讨论，并指出了当前面临的主要挑战。最后，文章展望了量子FFT算法的未来发展方向和研究前沿，强调了该领域在量子信息科学中的潜力和重要性。

# 关键字
量子计算；频率分析；快速傅里叶变换；量子位；量子频谱分析；理论挑战

参考资源链接：[蝶形运算：基-2 FFT算法详解与计算优化](https://wenku.csdn.net/doc/3t519wzvdu?spm=1055.2635.3001.10343)
# 1. 量子计算与频率分析基础

## 1.1 量子计算简介

量子计算是一种基于量子力学原理的计算方式，与传统的经典计算有着本质的不同。其基本单位是量子比特（qubit），不同于经典计算的0或1，qubit可以处于0和1的叠加状态，这使得量子计算具有极高的并行处理能力。

## 1.2 频率分析的重要性

频率分析是一种将信号或数据转换为其频率成分的过程，是许多科学和工程领域中的一个基本工具。在量子计算中，频率分析可以帮助我们理解和操纵量子信息，为量子计算的进一步发展提供理论基础。

## 1.3 量子计算与频率分析的关系

量子计算与频率分析的关系主要体现在快速傅里叶变换（FFT）算法上。FFT是频率分析的核心算法，而在量子计算中，如何将FFT算法量子化，使其能够在量子计算机上运行，是一个重要的研究方向。

# 2. 快速傅里叶变换(FFT)算法概述

## 一、FFT算法的起源与重要性
快速傅里叶变换（FFT）是数字信号处理领域的一项革命性技术。它的出现极大地促进了信号分析的效率，尤其是在需要处理大量数据的情况下。FFT算法的核心思想是通过减少离散傅里叶变换（DFT）的计算复杂度，从而实现快速运算。

### 历史背景
傅里叶变换由法国数学家让-巴普蒂斯特·约瑟夫·傅里叶于1822年提出，其基本思想是将任何复杂的信号分解为一系列简单的正弦波。传统的傅里叶变换在处理信号时，计算量巨大，主要因为其计算复杂度为O(N^2)。FFT算法则将这个复杂度降低到O(NlogN)，通过这种方式，FFT算法在实际应用中的效率得到了显著提升。

### 算法的重要性
FFT算法的重要性在于它几乎成为了现代数字信号处理不可或缺的一部分。在通信、音频处理、图像分析等领域中，FFT为快速获取信号频谱提供了可能，这在快速原型开发和实时系统中尤为关键。

## 二、FFT算法的工作原理
FFT算法的工作原理基于一个关键的数学发现——DFT的对称性和周期性。这些特性允许将原始的DFT表达式分解为更小的子集，通过递归或迭代的方式进行快速计算。

### 算法的核心概念
FFT算法依赖于几个核心概念，例如位反转（bit-reversal）和蝴蝶运算（butterfly operation）。位反转是指将索引按照二进制反转的方式来重新排列，而蝴蝶运算则是实现DFT快速计算的基本单元。

### 算法的关键步骤
FFT算法的关键步骤可以分解为以下几点：
1. 对输入数据进行位反转排序。
2. 分解原始的DFT为一系列更小的DFT。
3. 应用蝶形运算逐步计算出结果。

### 具体实现步骤
1. 输入数据进行位反转排序，以确保计算过程的效率。
2. 将数据分成较小的块，然后对每个块应用蝶形运算。
3. 递归或迭代地处理每个小块，直到得到最终的FFT结果。

## 三、FFT算法的实现细节
FFT算法的实现涉及到了许多重要的细节，这些细节决定了算法的效率和适用性。在实际编码实现中，有多种优化策略可以进一步提升FFT算法的性能。

### 缓存优化策略
由于FFT算法在实际运行中涉及到大量的重复数据访问，合理的缓存优化策略至关重要。利用现代处理器的缓存机制，通过预加载和数据重用，可以显著提高缓存命中率，从而提升算法性能。

### 并行计算与多线程
现代计算设备通常具有多核处理器，这为FFT算法的并行计算提供了硬件基础。通过多线程技术，可以将FFT算法分割成多个独立的子任务，同时在不同的处理器核心上运行，以此提高计算速度。

## 四、代码实现与分析
在这一部分，我们将通过一段具体的FFT实现代码，来详细解释其背后的逻辑与实现细节。

import numpy as np
from scipy.fftpack import fft

def compute_fft(signal):
    N = len(signal)
    # 这里使用的是scipy库中的fft函数，它利用了底层的FFTW算法
    fft_result = fft(signal)
    return fft_result

signal = np.random.rand(1024)  # 生成一个随机信号
fft_result = compute_fft(signal)

print(fft_result)

### 代码逻辑解读
上述Python代码使用了`scipy`库中的`fft`函数，该函数是基于FFTW（Fastest Fourier Transform in the West）算法的实现。`compute_fft`函数接收一个信号数组作为输入，并计算其快速傅里叶变换。由于`fft`函数是高度优化的，所以不需要手动进行位反转排序和蝶形运算，它们都是在底层自动完成的。

### 参数说明与优化
在`compute_fft`函数中，`signal`是待处理的信号数组，其长度为`N`。`N`需要为2的幂次，因为这是大多数FFT实现所要求的。如果长度不满足要求，可以通过补零的方式进行调整。

### 扩展性说明
此代码可以很容易地进行扩展，例如加入信号的预处理和后处理步骤，或者并行化处理多个信号，以及集成到更大的信号处理系统中。此外，为了提高性能，可以考虑使用多线程或多进程来处理大规模的数据集。

在了解了FFT算法的工作原理、实现细节、代码分析之后，我们为理解其在量子计算中的应用打下了坚实的基础。下一章节，我们将探索FFT算法如何与量子计算相结合，并讨论其在量子频谱分析中的应用实践。

# 3. 量子位与量子频谱分析

量子位（qubit）是量子计算中的基本信息单位，不同于传统的二进制位（bit），它能够同时处于0和1的量子叠加态。量子频谱分析则是一种利用量子计算的原理进行频率分析的方法。本章节将深入探讨量子位的特性以及它如何应用于量子频谱分析，并展示相关实例和应用场景。

## 量子位的特性与操作

### 量子位的叠加态和纠缠

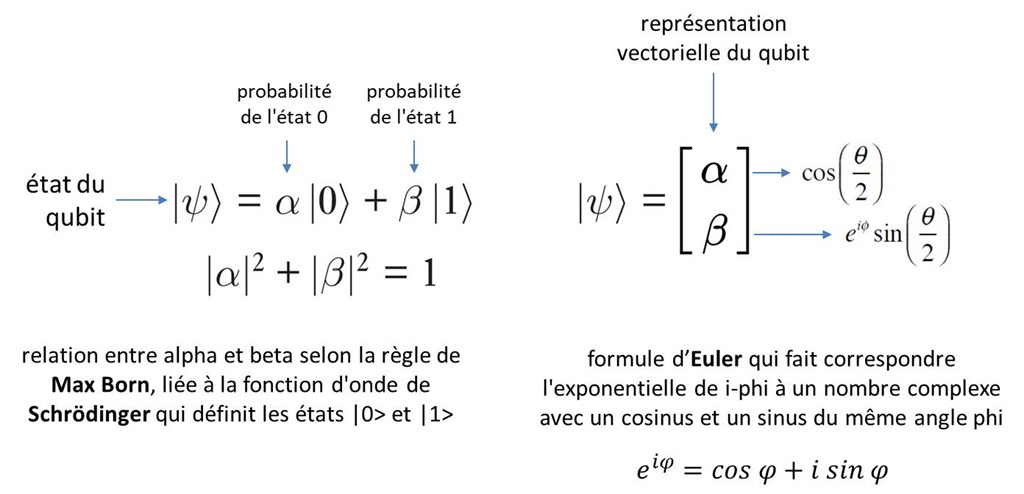
量子位的核心特性之一是叠加态。不同于传统比特的二元状态，量子位可以处于 |0⟩ 和 |1⟩ 的叠加态，用数学表达式可表示为 |ψ⟩ = α|0⟩ + β|1⟩，其中α和β是复数概率幅，它们的模平方分别代表测量得到0或1的概率。

另一个重要特性是量子纠缠，量子位之间可以存在一种特殊的关联，使得对其中一个量子位的测量会即时影响到与之纠缠的其他量子位的状态，无论它们相隔多远。

### 量子门的操作

量子计算中的基本操作是通过量子门来实现的。量子门作用于一个或多个量子位，执行各种逻辑操作。例如，Hadamard门（H门）可以把量子位从 |0⟩ 或 |1⟩ 状态转换到叠加态：

import numpy as np

# 定义Hadamard门矩阵
H = (1/np.sqrt(2)) * np.array([[1, 1], [1, -1]])

# 作用在初始状态 |0⟩ 上
initial_state = np.array([1, 0])
h_state = np.dot(H, initial_s