【并行计算中的FFT应用】：大数据处理加速的秘密武器


# 摘要
本文系统地解析了并行计算与快速傅里叶变换（FFT）的关系，阐述了FFT算法的理论基础和并行FFT算法的设计与实现。文章首先介绍并行计算与FFT的基础概念，随后深入探讨了FFT算法的理论基础，包括离散傅里叶变换（DFT）原理和数学优化。第三章重点介绍了并行FFT算法的设计与实现，包括并行计算环境的构建，以及并行FFT算法策略和实际案例分析。第四章探讨了FFT在大数据处理、信号处理和图像处理中的应用实践。最后，第五章展望了并行FFT的未来发展趋势，包括新兴技术的影响、算法优化与创新，以及在不同领域的扩展应用潜力。

# 关键字
并行计算；快速傅里叶变换；离散傅里叶变换；算法设计；大数据处理；量子计算

参考资源链接：[蝶形运算：基-2 FFT算法详解与计算优化](https://wenku.csdn.net/doc/3t519wzvdu?spm=1055.2635.3001.10343)
# 1. 并行计算与FFT概念解析

并行计算代表了一类计算方法，它通过多处理器或计算机同时执行多个计算任务来加快计算速度。这种技术在处理大型数据集和复杂计算模型时至关重要，尤其在科学和工程领域中得到了广泛应用。

快速傅里叶变换（FFT）是并行计算中常用于信号处理、图像分析和许多其他领域的算法。它能够将信号从时域转换到频域，极大地加快了傅里叶变换的计算过程，从而在实际应用中实现了高效的资源利用和性能提升。

FFT的概念建立在傅里叶变换的基础上，它能够减少变换的运算量，从原本的O(N^2)复杂度降低到O(NlogN)，其中N代表样本数量。这种高效的算法不仅在理论上具有重要意义，也为实际应用中的复杂问题提供了有效的解决方案。在后续章节中，我们将更深入地探讨FFT的理论基础及其并行计算实现。

# 2. FFT算法的理论基础

## 2.1 离散傅里叶变换(DFT)原理

### 2.1.1 DFT的基本定义和数学公式

离散傅里叶变换（Discrete Fourier Transform, DFT）是将时域的离散信号转换到频域的一种算法。DFT在信号处理、图像分析、量子物理等多个领域都有广泛应用。DFT的核心思想是通过复数运算来分析信号在不同频率下的组成。

数学上，对于一个长度为N的复数序列 \(X = [x_0, x_1, \ldots, x_{N-1}]\)，其DFT定义为：

\[
X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-\frac{i2\pi}{N}kn} \quad \text{for } k = 0, 1, \ldots, N-1
\]

其中，\(X_k\) 是频域表示中的第 \(k\) 个元素，\(n\) 是时域中的样本索引，\(i\) 是虚数单位。

代码块展示了一个简单的Python实现DFT的例子：

import numpy as np

def dft(x):
    N = len(x)
    n = np.arange(N)
    k = n.reshape((N, 1))
    e = np.exp(-2j * np.pi * k * n / N)
    return np.dot(e, x)

# Example usage:
x = np.array([1.0, 2.0, 3.0, 4.0])
X = dft(x)
print(X)

执行逻辑说明：该代码首先导入numpy库以利用其数组操作和复数运算的功能。`dft` 函数计算输入序列 `x` 的DFT。通过创建两个索引数组 `n` 和 `k` 并构造复指数矩阵 `e`，最后通过点乘计算得出DFT结果。

参数说明：`x` 参数代表输入的复数序列；`N` 参数为序列长度；`n` 和 `k` 是索引数组；`e` 是构造的复指数矩阵。

### 2.1.2 DFT的计算复杂性分析

DFT的计算复杂度为 \(O(N^2)\)，这在N较大时会导致计算效率低下。对于长度为N的序列，DFT需要进行\(N^2\)次复数乘法和\(N(N-1)\)次复数加法。随着N的增加，计算量呈指数级增长，这对于处理大规模数据集构成了一个显著的挑战。

优化策略通常包括：减少不必要的计算，例如使用对称和周期性质；使用快速傅里叶变换FFT进一步优化计算过程，其复杂度可降低到\(O(N\log N)\)。

## 2.2 快速傅里叶变换(FFT)的算法演进

### 2.2.1 FFT的发展历程

快速傅里叶变换（Fast Fourier Transform, FFT）是DFT的快速算法。由Cooley和Tukey在1965年提出，它是数字信号处理领域的里程碑，极大地推动了该领域的发展。

最初，FFT主要用于处理和分析周期性信号，但随着算法的演进和优化，FFT的适用范围已经大大扩展。现在的FFT算法已经被设计为能够适应并行计算环境，并且有着多种不同的实现方式以应对不同的应用场景和性能要求。

### 2.2.2 常见的FFT算法变种

一种常见的FFT变种是递归实现的FFT，它将原始的DFT分解为更小的DFT问题，然后逐步求解。这种方法将复杂数组的分割和合并结合起来，显著提高了计算效率。

另一种变种是基于迭代的FFT，例如基2FFT和基4FFT，这种迭代方法利用了DFT的分裂性质，适用于特定大小的数据集。与递归版本相比，迭代FFT通常在内存使用和计算效率方面有优势。

例如，基2FFT适用于数据点数为2的幂次的情况。当数据集大小不符合2的幂次时，可以通过填充零值来调整数据点数，使其满足要求。

## 2.3 FFT算法的数学优化

### 2.3.1 数学推导和优化策略

FFT算法的数学推导主要基于DFT的对称性和周期性，利用这些性质减少乘法运算次数。FFT算法的关键在于分治策略，即将长序列的DFT分解为较短序列的DFT，这减少了整体的计算量。

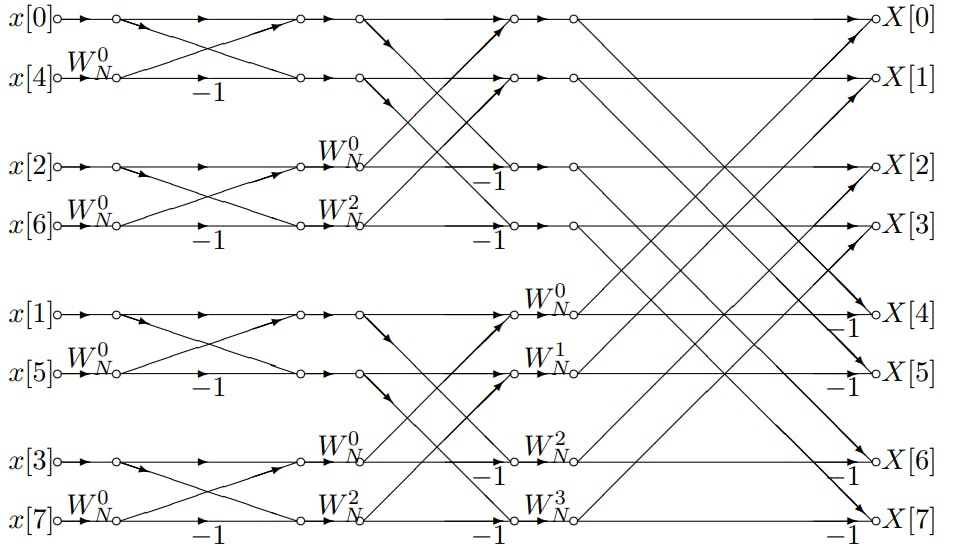
优化策略中，一个重要的方法是将原始的DFT分组为偶数项和奇数项的两部分，这样可以递归地分解成更小的问题。这被称为“蝴蝶”运算，是FFT算法中最为核心的部分。

### 2.3.2 算法在不同场景下的应用效率分析

在不同的应用场景中，FFT算法的应用效率取决于数据点的数量和硬件性能。例如，在处理实时信号时，需要快速响应的FFT实现，而数据预处理通常需要较高精度和较高吞吐量的FFT实现。

在高维数据处理中，例如图像和视频分析，FFT的多维变种被广泛用于快速特征提取和压缩。在这些场景下，效率通常体现在算法的可扩展性以及对不同硬件架构的适应性上。

接下来章节将探讨并行FFT算法的设计与实现，这是在现代高性能计算领域中实现FFT高效运算的关键。

# 3. 并行FFT算法的设计与实现

## 3.1 并行计算环境的构建

### 3.1.1 硬件架构与并行计算

在并行计算领域，硬件架构的选择对于算法的性能有着决定性的影响。当前，常见的并行计算硬件平台包括高性能计算集群、多核处理器、GPU加速计算单元以及近年来越发热门的FPGA加速器。

高性能计算集群是由多台计算机组成，通过高速网络连接在一起，实现计算任务的分布式处理。