【FFT算法在音频处理中的应用】：声音频谱分析的幕后英雄


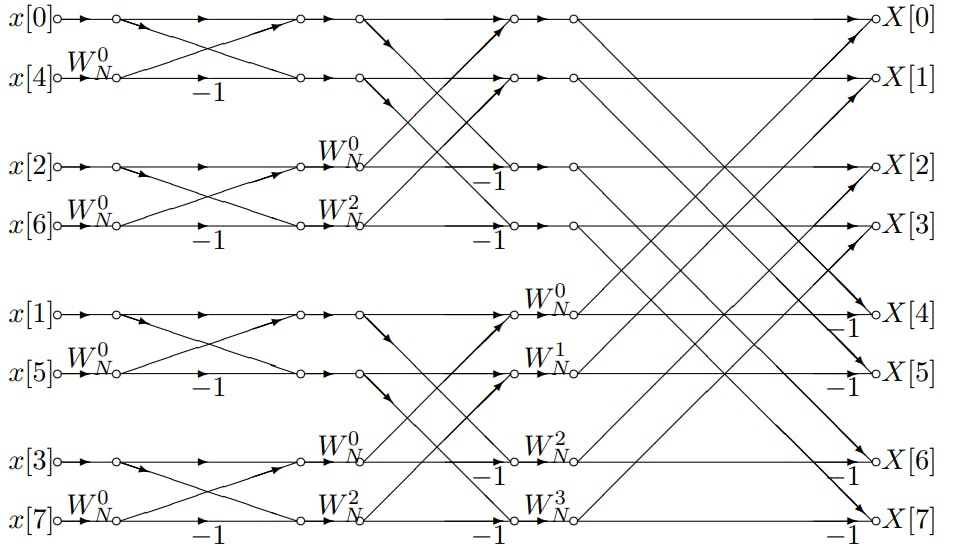
# 摘要
本文深入探讨了快速傅里叶变换（FFT）算法及其在音频信号处理中的广泛应用。首先，概述了FFT算法的基本原理和音频信号处理的基础知识，随后详细介绍了FFT算法在音频频谱分析中的实现方法和高级应用，包括声音增强、音频压缩编码和特征提取。文章通过案例分析，展示了FFT算法在实时音频频谱分析器构建和声音分类识别系统中的实际应用，并对其未来的发展趋势和音频处理领域的新兴技术进行了展望。本文旨在为音频处理领域的研究者和工程师提供一个全面的FFT应用指南，并促进该领域技术的进一步创新和发展。

# 关键字
FFT算法；音频信号处理；频谱分析；声音增强；音频压缩编码；特征提取

参考资源链接：[蝶形运算：基-2 FFT算法详解与计算优化](https://wenku.csdn.net/doc/3t519wzvdu?spm=1055.2635.3001.10343)
# 1. FFT算法概述

快速傅里叶变换（FFT）是一种非常高效计算离散傅里叶变换（DFT）及其逆变换的算法。它在信号处理、图像处理和音频分析等领域有着广泛的应用。

## 1.1 FFT算法的重要性

FFT算法的重要性在于其大大降低了DFT的计算复杂度，从O(N^2)降到了O(NlogN)，其中N是样本数量。这个改进使得在实际应用中，对大规模数据进行频谱分析成为可能。

## 1.2 FFT算法的历史背景

FFT算法最早由James Cooley和John Tukey在1965年提出，后来成为了数字信号处理领域的核心技术。在FFT之前，DFT的计算复杂度过高，严重限制了其在实际中的应用。

## 1.3 FFT算法的应用领域

FFT不仅在音频频谱分析中有广泛应用，还被用于图像压缩（如JPEG格式）、通信信号处理、雷达信号分析等多个领域。它的高效性使得实时信号处理成为可能，推动了相关技术的发展。

(* 示例：在Mathematica中实现FFT算法 *)
fftSignal = Fourier[listOfSignalData];

通过上述公式，在Mathematica中我们可以轻松地对一组信号数据进行FFT变换。这只是FFT算法在实际中应用的一个简单例子。在后续章节中，我们将深入探讨FFT算法在音频处理中的应用和优化。

# 2. 音频信号处理的基础知识

音频信号处理是数字信号处理领域的一个重要分支，它涉及到声音信号的获取、表示、存储、传输和重建等过程。音频信号处理的基础知识是深入理解FFT算法及其它音频分析工具的前提。

## 2.1 音频信号的基本概念

### 2.1.1 声音的物理特性

声音是一种机械波，它通过介质（如空气、水或固体）传播。声波的频率决定了我们所感知的声音的音高，而振幅决定了声音的响度。在数字音频信号处理中，声音的这些物理特性可以通过采样和量化转换成数字形式进行处理。

### 2.1.2 数字音频信号的表示

数字音频信号是模拟声音信号经过模数转换后的结果，它由一系列离散的数值组成。每个数值称为样本(sample)，而这些样本在时间上均匀间隔，即采样率(sampling rate)。每个样本用一定数量的比特(bit)表示，这个数量称为采样深度(sample depth)或位深(bit depth)。采样率和位深共同决定了数字音频的质量。

## 2.2 频谱分析的理论基础

频谱分析是音频信号处理的核心技术之一，它将信号分解为不同频率的分量，帮助我们深入理解信号的频率内容。

### 2.2.1 频谱分析的数学原理

频谱分析基于傅里叶级数和傅里叶变换的数学原理。傅里叶级数告诉我们，任何周期函数都可以表示为一系列的正弦波和余弦波的和。而傅里叶变换则是将非周期信号分解为连续的频率成分。

### 2.2.2 离散傅里叶变换（DFT）

离散傅里叶变换是傅里叶变换在离散信号上的实现。DFT将一个长度为N的复数序列转换成另一个长度为N的复数序列。每个输出值表示原序列中的数据在特定频率下的复振幅，通过它可以得到信号的频谱信息。DFT的计算复杂度为O(N^2)，这个复杂度对于长序列的处理是非常耗时的。

## 2.3 FFT算法的数学原理

快速傅里叶变换(FFT)是一种高效计算DFT的算法，其核心在于减少计算量。

### 2.3.1 DFT的计算复杂度

在没有FFT优化的情况下，DFT的直接计算需要进行N^2次复数乘法和(N-1)^2次复数加法。对于长序列而言，这种直接计算是非常耗时的，尤其是当N非常大时。

### 2.3.2 FFT算法的优化路径

FFT算法通过分解复数乘法操作、利用对称性质、采用迭代计算等方法，将DFT的计算复杂度降低到O(NlogN)。这样，FFT在处理大规模数据时相比于DFT可以节约大量的计算时间。

在接下来的章节中，我们将进一步探讨FFT算法在音频频谱分析中的具体实现和应用，以及如何通过软件库和工具来方便地使用FFT算法进行音频处理。

# 3. FFT算法在音频频谱分析中的实现

## 3.1 FFT算法的软件实现

### 3.1.1 快速傅里叶变换的步骤

快速傅里叶变换（FFT）作为数字信号处理的核心算法之一，其关键在于利用信号的对称性和周期性来简化离散傅里叶变换（DFT）的计算。一个基本的FFT算法通常遵循以下步骤：

1. **信号分解**：将输入的信号序列分为偶数和奇数索引的部分。
2. **递归处理**：将得到的两个子序列分别进行DFT运算。
3. **蝶形运算**：利用DFT的性质进行一系列的加法和乘法运算（蝶形运算），以减少计算量。
4. **合并结果**：结合步骤2和步骤3的结果，得到最终的FFT结果。

#### 代码示例

下面是一个简单的Python代码示例，演示了如何实现一个基本的FFT算法：

import numpy as np

def fft(x):
    N = len(x)
    if N <= 1: return x
    even = fft(x[0::2])
    odd = fft(x[1::2])
    T = [np.exp(-2j * np.pi * k / N) * odd[k] for k in range(N // 2)]
    return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)]

# 示例输入
x = np.random.rand(8)
# 执行FFT算法
result = fft(x)
print(result)

在这个代码块中，`fft`函数首先检查输入序列的长度，如果长度小于或等于1，则直接返回序列。对于长度大于1的序列，它将序列分成偶数和奇数索引两部分，分别对这两部分递归地执行FFT运算。然后通过蝶形运算组合结果，最终返回完整的FFT变换结果。

### 3.1.2 FFT算法的常见库和工具

在实际应用中，由于FFT算法复杂度较高，通常会使用成熟的数学库或工具来执行FFT操作。下面列举一些常见的FFT实现工具：

- **NumPy**：Python编程语言中最常用的数学库之一，它提供了一个高效的FFT实现函数`numpy.fft.fft`。
- **FFTW**：被广泛认为是最快的C语言FFTW库，支持多维数据的FFT。
- **Intel MKL**：英特尔的数学核心库，包含了许多优化过的数学运算函数，包括FFT。
- **MathWorks MATLAB**：在工程和科学领域广泛应用的编程环境，提供内置的FFT函数。

这些工具中，大多数都是高度优化的，能够利用多线程和指令级并行来加速计算。

#### 表格展示

| 库/工具名称 | 编程语言支持 | 特点 |
| ------------ | -------------- | ---- |
| NumPy | Python | 高效、易用、跨平台 |
| FFTW | C/C++ | 高性能FFT算法库 |
| Intel MKL | C/C++ | 高度优化、多线程 |
| MATLAB | MATLAB语言 | 易于使用、集成度高 |

## 3.2 频谱分析的实践应用

### 3.2.1 音频信号的时域转频域分析

音频信号分析是音频处理中的一个核心环节。通常，我们首先在时域中对音频信号进行采样和表示，然后通过FFT将信号从时域转换到频域。在频域中，音频信号的频率内容得以清晰地展现。

频域分析的一个关键应用是对音频信号的频率成分进行分解，进而进行频率过滤、声音合成以及音质分析等操作。例如，通过分析FFT变换的结果，我们可以识别出音频信号中的主要频率成分，实现如高通、低通或带通等滤波器的设计。

#### 代码示例

以下代码使用了Python的NumPy库，演示了如何将音频信号从时域转换到频域：

import numpy as np
import matplotlib.pyplot as plt

# 假设x是已经加载的音频信号样本数据
x = ... # 加载音频信号数据的代码
N = len(x)
# 执行FFT并获取频谱
yf = np.fft.fft(x)
xf = np.linspace(0.0, 1.0/(2.0*N), N//2)

# 绘制单边频谱图
plt.figure()
plt.plot(xf, 2.0/N * np.abs(yf[:N//2]))
plt.title('Single-Sided Amplitude Spectrum of Audio')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.show()

在这个示例中，我们首先加载了音频信号样本数据`x`，然后使用`np.fft.fft`函数计算其FFT变换。通过`np