【FFT算法优化技巧】：提升效率的十大实用策略，立刻行动！


# 摘要
快速傅里叶变换（FFT）算法是一种高效的离散傅里叶变换（DFT）计算方法，广泛应用于信号处理、图像分析、音频技术等多个领域。本文全面概述了FFT算法的基础知识、数学原理以及实际应用。首先介绍了FFT算法的基本概念和数学背景，然后深入探讨了其在信号处理中的关键作用，如频谱分析和信号滤波。接着分析了FFT算法的性能瓶颈和优化策略，包括时间复杂度的降低、空间复杂度的优化以及数据对齐的重要性。文章还讨论了编程语言的选择和高效算法实现技巧，并通过实践案例展示了FFT在声音和图像处理中的具体应用。最后，探讨了新兴技术对FFT算法的影响和未来发展趋势。

# 关键字
FFT算法；信号处理；离散傅里叶变换；性能优化；频谱分析；算法实现

参考资源链接：[蝶形运算：基-2 FFT算法详解与计算优化](https://wenku.csdn.net/doc/3t519wzvdu?spm=1055.2635.3001.10343)
# 1. FFT算法基础概述

快速傅里叶变换（Fast Fourier Transform，FFT）是数字信号处理中不可或缺的算法，它提供了一种高效计算离散傅里叶变换（Discrete Fourier Transform，DFT）及其逆变换的方法。FFT极大地降低了传统DFT所需的计算量，从而加快了信号处理的频率分析速度。通过将时间复杂度从O(N^2)降低到O(NlogN)，FFT不仅适用于实时系统，还推动了现代通信、图像处理等领域的技术进步。

# 2. FFT算法的数学原理和应用

## 2.1 DFT与FFT的数学关系

### 2.1.1 离散傅里叶变换的定义和性质

离散傅里叶变换（DFT）是数字信号处理中的一个基本工具，它允许我们将时域信号转换到频域。对于一个长度为N的复数序列 {x[n]}，其DFT定义为：

\[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i 2 \pi k n / N} \]

其中 \( i \) 是虚数单位，\( k = 0, 1, ..., N-1 \)。

DFT有几个重要的性质，包括：

- 线性：DFT是线性变换，即两个序列之和的DFT等于各自DFT之和。
- 周期性：DFT的结果是周期的，具有周期N。
- 对称性：对于实数序列，DFT是共轭对称的。

DFT的计算复杂度为\( O(N^2) \)，这使得它在实际应用中效率较低，尤其是在处理大数据集时。

### 2.1.2 快速傅里叶变换的起源和基本原理

快速傅里叶变换（FFT）是对DFT的一种高效计算方法。其基本思想是利用DFT的周期性和对称性来减少计算量。FFT最早由J.W. Cooley和J.W. Tukey于1965年提出，使得DFT的计算复杂度从\( O(N^2) \)降低到\( O(N \log N) \)。

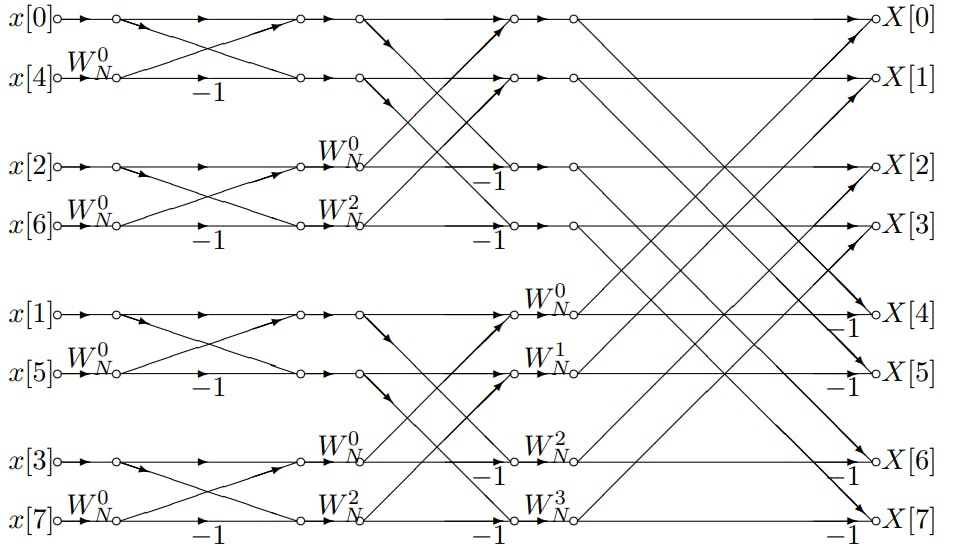
FFT算法的基本原理可以通过分治策略来理解。将序列分成两部分，一部分包含所有的偶数索引项，另一部分包含所有的奇数索引项。通过递归地对这两部分分别应用DFT，然后将结果合并，可以得到整个序列的DFT。通过这样的方法，FFT能够减少重复计算的次数，从而提高计算效率。

### 2.2 FFT算法在信号处理中的作用

#### 2.2.1 信号频谱分析

FFT在信号处理中的一个重要应用是进行频谱分析。频谱分析是将信号分解为不同频率成分的过程，它可以帮助我们了解信号的频率结构和特性。

例如，在音频处理中，我们可能想要知道一个音乐片段中不同频率的成分如何分布。通过将信号通过FFT变换到频域，我们可以得到各个频率成分的幅度和相位信息，从而对信号进行更深入的分析。

#### 2.2.2 信号滤波与恢复

FFT也可以用于信号的滤波和恢复。滤波是信号处理中的一项基本操作，它可以帮助我们提取有用信息，同时去除噪声和其他不需要的信号成分。

假设我们有一个包含噪声的信号，通过FFT将信号变换到频域，我们可以设计一个滤波器来除去某些特定频率的成分。之后，通过逆FFT变换回时域，我们得到一个滤波后的信号。

此外，FFT还可以用于信号的恢复，例如在数字通信中恢复被干扰的信号。通过分析信号的频谱，并进行适当处理，然后逆变换回时域，我们可以恢复出原始信号。

在下一部分中，我们将探讨FFT算法的性能瓶颈与优化，特别是如何处理信号处理中的实际问题。

# 3. FFT算法的性能瓶颈与优化

## 3.1 时间复杂度分析

### 3.1.1 传统FFT算法的时间复杂度

传统的FFT算法是通过分治策略将复杂的DFT运算分解为较小的DFT运算，再通过蝶形运算将结果组合起来。在计算一个长度为N的序列的FFT时，经典的Cooley-Tukey算法将问题规模递归地分解为两个N/2的子问题。对于最简单的情况，即N为2的幂，FFT的时间复杂度为O(N log N)。这个时间复杂度是由递归的深度（log N）和每一层递归中的操作数（N）决定的。

然而，在实际应用中，原始FFT算法存在一定的性能瓶颈。主要问题是数据依赖性导致的低缓存命中率和流水线效率低下，从而影响整体性能。举例来说，蝶形运算中一个数据点可能被多次读取，如果数据不能有效存储在高速缓存中，将导致频繁的内存访问，从而降低算法执行速度。

graph TD;
    A[FFT调用] --> B[分解为子问题];
    B --> C[递归计算子问题];
    C --> D[蝶形运算组合结果];
    D --> E[返回FFT结果];

### 3.1.2 现代FFT算法的时间性能优化

现代FFT算法通过多种技术来优化时间复杂度，尤其是在大数据集上的性能。优化策略包括使用混合基数算法、并行计算、以及优化内存访问模式。混合基数算法允许在不同基数之间进行选择，以适应不同的硬件架构和数据集特点。

并行计算是通过多线程或多核处理器同时执行多个计算任务，减少总体执行时间。现代处理器通常具备SIMD（单指令多数据）指令集，这允许单个指令操作多个数据点。这在FFT算法中特别有用，因为可以一次对多个数据点进行蝶形运算。

代码示例：

//