正弦波揭秘：从本质到应用的全面解析

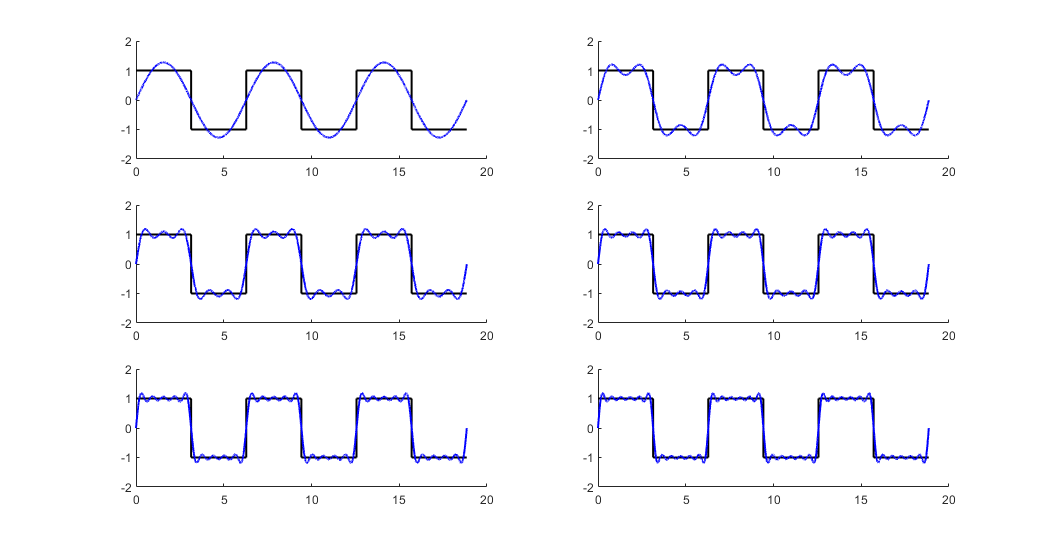
# 1. 正弦波的数学本质**

正弦波是一种周期性的函数，可以用正弦函数表示：y = A * sin(ωt + φ)。其中，A 是幅度，ω 是角频率，t 是时间，φ 是相位。

正弦波的幅度表示波峰和波谷之间的距离，角频率表示波的周期，相位表示波在时间轴上的偏移。这些参数共同决定了正弦波的形状和行为。

正弦波具有线性性，这意味着两个正弦波可以叠加在一起，形成一个新的正弦波。叠加后的波的幅度和相位取决于原始波的幅度和相位。

# 2. 幅度和相位

**频率**

正弦波的频率表示波形在单位时间内重复的次数，单位为赫兹 (Hz)。频率决定了波形的周期，即两个波峰或波谷之间的距离。频率越高，周期越短，波形变化越快。

**幅度**

正弦波的幅度表示波形的最大值和最小值之间的差值。幅度决定了波形的强度或音量。幅度越大，波形越强。

**相位**

正弦波的相位表示波形在特定时间点的偏移量。相位通常以度或弧度表示。相位决定了波形的起点，即波峰或波谷相对于参考点的偏移。

### 频率、幅度和相位的测量

**频率测量**

频率可以通过示波器、频谱分析仪或示波器等仪器测量。这些仪器可以显示波形的周期，从而计算出频率。

**幅度测量**

幅度可以通过示波器、电压表或功率计等仪器测量。这些仪器可以显示波形的最大值和最小值，从而计算出幅度。

**相位测量**

相位可以通过示波器、相位计或锁相环等仪器测量。这些仪器可以比较波形与参考信号的相位差，从而计算出相位。

### 频率、幅度和相位的应用

正弦波的频率、幅度和相位在许多实际应用中都很重要，例如：

* **交流电系统：**频率和幅度决定了交流电的电压和电流特性。
* **声学：**频率决定了声音的音高，幅度决定了声音的音量。
* **光学：**频率决定了光的颜色，相位决定了光的偏振。

# 3.1 正弦波在交流电中的作用

正弦波在交流电中扮演着至关重要的角色，它描述了交流电的电压和电流随时间变化的规律。

**交流电的产生**

交流电是通过发电机产生的，发电机利用法拉第电磁感应定律将机械能转化为电能。当发电机的转子在定子中旋转时，会产生交变的磁场，根据法拉第电磁感应定律，交变的磁场会在定子绕组中感应出交变的电动势，从而产生交流电。

**正弦波的特征**

交流电的电压和电流都是正弦波形式，其特征如下：

- **频率：**正弦波的频率表示波形在单位时间内重复的次数，单位为赫兹（Hz）。
- **幅度：**正弦波的幅度表示波形的最大值，单位为伏特（V）或安培（A）。
- **相位：**正弦波的相位表示波形在特定时刻与参考点的偏移，单位为度或弧度。

**交流电的传输**

交流电通过输电线路进行传输，正弦波形式的交流电具有以下优点：

- **高效率：**正弦波的能量分布均匀，传输损耗较小。
- **易于变压：**正弦波的电压和电流可以通过变压器轻松地升压或降压。
- **抗干扰能力强：**正弦波的波形稳定，不易受到谐波干扰。

**交流电的应用**

交流电广泛应用于各种电气设备和系统中，包括：

- **家用电器：**冰箱、空调、洗衣机等家用电器都使用交流电。
- **工业设备：**电动机、变压器、发电机等工业设备也使用交流电。
- **照明系统：**路灯、室内照明等照明系统也使用交流电。

### 3.2 正弦波在声学中的应用

正弦波在声学中也具有重要的应用，它描述了声音波的振动规律。

**声音的产生**

声音是由物体振动产生的，当物体振动时，会带动周围的空气分子振动，从而产生声波。声波是一种机械波，它在空气中以波的形式传播。

**正弦波的特征**

声波的振动可以表示为正弦波，其特征如下：

- **频率：**声波的频率表示波形在单位时间内重复的次数，单位为赫兹（Hz）。
- **幅度：**声波的幅度表示波形的最大值，单位为帕斯卡（Pa）。
- **相位：**声波的相位表示波形在特定时刻与参考点的偏移，单位为度或弧度。

**声音的传播**

声波在空气中以波的形式传播，其传播速度与空气的温度和密度有关。正弦波的传播速度可以表示为：

v = f * λ

其中：

- v 是传播速度
- f 是频率
- λ 是波长

**声音的应用**

正弦波在声学中广泛应用于：

- **音乐：**音乐中的音符都可以表示为正弦波，不同的音符对应不同的频率。
- **超声波：**超声波是一种频率高于人耳可听范围的声波，广泛应用于医疗成像、工业检测等领域。
- **声纳：**声纳利用声波在水中的传播特性来探测水下物体。

### 3.3 正弦波在光学中的应用

正弦波在光学中也具有重要的应用，它描述了光波的振动规律。

**光的产生**

光是由原子或分子的电子跃迁产生的，当电子从高能级跃迁到低能级时，会释放出能量以光子的形式。光波是一种电磁波，它在真空中以波的形式传播。

**正弦波的特征**

光波的振动可以表示为正弦波，其特征如下：

- **频率：**光波的频率表示波形在单位时间内重复的次数，单位为赫兹（Hz）。
- **幅度：**光波的幅度表示波形的最大值，单位为伏特/米（V/m）。
- **相位：**光波的相位表示波形在特定时刻与参考点的偏移，单位为度或弧度。

**光的传播**

光波在真空中以波的形式传播，其传播速度为光速，约为 3 x 10^8 m/s。正弦波的传播速度可以表示为：

v = f * λ

其中：

- v 是传播速度
- f 是频率
- λ 是波长

**光的应用**

正弦波在光学中广泛应用于：

- **激光：**激光是一种高度相干的正弦波光，广泛应用于光通信、激光加工等领域。
- **光纤通信：**光纤通信利用正弦波光的传输特性来实现高速数据传输。
- **光谱学：**光谱学利用正弦波光的吸收和发射特性来分析物质的组成和结构。

# 4. 正弦波的数字化与处理**

正弦波是自然界和工程领域中常见的波形，其数字化与处理在现代技术中具有广泛的应用。本章节将深入探讨正弦波的数字化方法、傅里叶分析以及滤波与处理技术。

## 4.1 正弦波的数字化方法

正弦波的数字化是指将连续的正弦波信号转换为离散的数字信号。常用的数字化方法有：

- **采样定理：**采样频率必须至少是信号最高频率的两倍，才能避免混叠。
- **奈奎斯特采样率：**满足采样定理的最低采样频率，等于信号最高频率的两倍。
- **均匀采样：**以均匀的时间间隔对信号进行采样。
- **非均匀采样：**以不均匀的时间间隔对信号进行采样，可提高采样效率。

**代码块：**

import numpy as np

# 正弦波参数
amplitude = 1.0  # 幅度
frequency = 100.0  # 频率
phase = 0.0  # 相位

# 采样率
sampling_rate = 2000.0

# 采样时间间隔
sampling_interval = 1.0 / sampling_rate

# 采样点数
num_samples = 1000

# 时间序列
time = np.linspace(0, (num_samples - 1) * sampling_interval, num_samples)

# 正弦波信号
signal = amplitude * np.sin(2 * np.pi * frequency * time + phase)

**逻辑分析：**

该代码块生成了一个采样率为 2000 Hz 的正弦波信号。采样时间间隔为 0.5 ms，采样点数为 1000。正弦波的幅度为 1.0，频率为 100 Hz，相位为 0。

## 4.2 正弦波的傅里叶分析

傅里叶分析是一种将信号分解为正弦波和余弦波分量的数学工具。对于正弦波信号，傅里叶分析可以确定其频率、幅度和相位。

**代码块：**

import numpy as np
from scipy.fftpack import fft

# 计算傅里叶变换
fft_result = fft(signal)

# 提取幅度谱
amplitude_spectrum = np.abs(fft_result)

# 提取相位谱
phase_spectrum = np.angle(fft_result)

# 频率分辨率
frequency_resolution = sampling_rate / num_samples

# 频率序列
frequencies = np.linspace(0, sampling_rate / 2, num_samples // 2)

**逻辑分析：**

该代码块使用 scipy.fftpack 库计算了正弦波信号的傅里叶变换。fft_result 是一个复数数组，其中实部表示幅度谱，虚部表示相位谱。amplitude_spectrum 和 phase_spectrum 分别提取了幅度谱和相位谱。frequency_resolution 表示频率分辨率，frequencies 表示频率序列。

## 4.3 正弦波的滤波与处理

滤波是去除信号中不需要的频率成分的过程。处理是指对信号进行各种操作，以增强其特征或提取有用信息。

**代码块：**

import numpy as np

# 低通滤波器
def lowpass_filter(signal, cutoff_frequency, sampling_rate):
    # 滤波器阶数
    order = 5

    # 设计滤波器
    b, a = signal.butter(order, cutoff_frequency / (sampling_rate / 2), btype='low')

    # 滤波
    filtered_signal = signal.filtfilt(b, a, signal)

    return filtered_signal

# 高通滤波器
def highpass_filter(signal, cutoff_frequency, sampling_rate):
    # 滤波器阶数
    order = 5

    # 设计滤波器
    b, a = signal.butter(order, cutoff_frequency / (sampling_rate / 2), btype='high')

    # 滤波
    filtered_signal = signal.filtfilt(b, a, signal)

    return filtered_signal

**逻辑分析：**

该代码块定义了低通滤波器和高通滤波器函数。这两个函数使用 scipy.signal 库中的 butter 函数设计滤波器，然后使用 filtfilt 函数进行滤波。cutoff_frequency 参数指定滤波器的截止频率，sampling_rate 参数指定采样率。

**参数说明：**

- cutoff_frequency：截止频率，单位为 Hz。
- sampling_rate：采样率，单位为 Hz。
- order：滤波器阶数，表示滤波器的极点和零点的数量。
- b：滤波器的分子多项式系数。
- a：滤波器的分母多项式系数。

# 5. 正弦波在现代技术中的应用

正弦波在现代技术中扮演着至关重要的角色，在无线通信、医疗成像和人工智能等领域有着广泛的应用。

### 5.1 正弦波在无线通信中的应用

在无线通信中，正弦波被用作载波，将信息调制到其上进行传输。由于正弦波的稳定性和易于处理，它非常适合用于无线通信。

**5.1.1 调制技术**

调制是将信息编码到载波上的过程。常见的调制技术包括：

- **调幅 (AM)：**将信息调制到载波的幅度上。
- **调频 (FM)：**将信息调制到载波的频率上。
- **调相 (PM)：**将信息调制到载波的相位上。

**5.1.2 天线**

天线是将电信号转换为电磁波并进行发射和接收的装置。正弦波在无线通信中通过天线进行发射和接收。

### 5.2 正弦波在医疗成像中的应用

在医疗成像中，正弦波被用作超声波和磁共振成像 (MRI) 的基础。

**5.2.1 超声波**

超声波是一种高频声波，可以穿透人体组织并反射回图像。正弦波被用于产生超声波，其频率和幅度决定了图像的分辨率和穿透深度。

**5.2.2 磁共振成像 (MRI)**

MRI 是一种利用强磁场和射频脉冲成像人体组织的技术。正弦波被用作射频脉冲，其频率和相位决定了图像的对比度和清晰度。

### 5.3 正弦波在人工智能中的应用

在人工智能中，正弦波被用于神经网络和机器学习算法。

**5.3.1 神经网络**

神经网络是一种受人脑启发的机器学习模型。正弦波被用作激活函数，将神经元的输入转换为输出。

**5.3.2 机器学习算法**

机器学习算法用于从数据中学习模式和做出预测。正弦波被用作特征提取器，从数据中提取有用的信息。