正弦波的数字化：采样与量化的奥秘

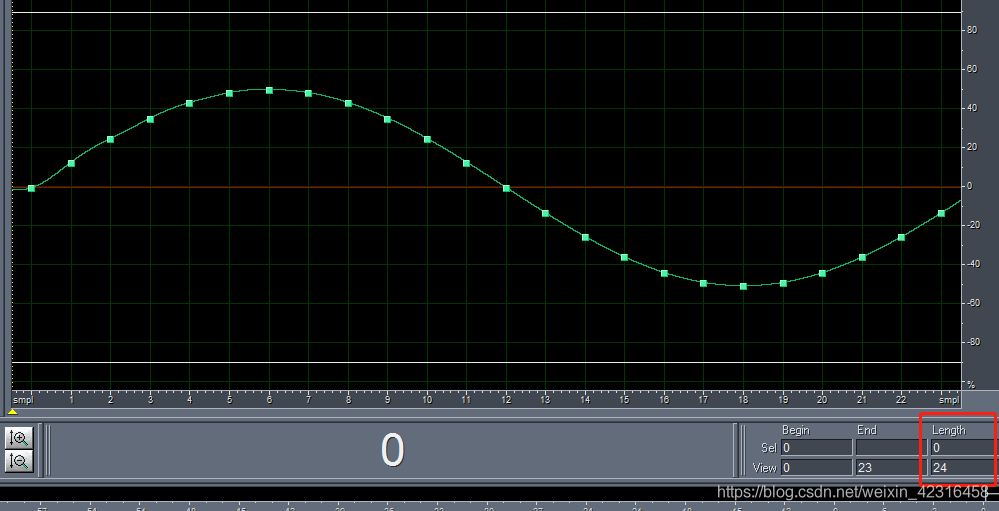
# 1. 正弦波的数字化概述**

数字化是将连续时间信号转换为离散时间信号的过程，而正弦波是连续时间信号中的一种常见类型。正弦波数字化涉及采样和量化两个基本步骤，这些步骤将连续时间正弦波转换为离散时间数字信号。

采样是指以一定频率对正弦波进行离散时间测量。采样率必须高于正弦波的最高频率分量，以避免混叠失真。量化是将采样值转换为离散幅度等级的过程。量化步长决定了数字信号的精度和量化噪声水平。

# 2. 采样理论

### 2.1 奈奎斯特采样定理

#### 2.1.1 采样频率与信号带宽

奈奎斯特采样定理规定，为了避免混叠，采样频率 **fs** 必须至少是信号最高频率 **fm** 的两倍：

fs >= 2 * fm

此定理确保采样后的信号包含原始信号的所有信息，并且不会出现混叠失真。

#### 2.1.2 采样率的选择

在实际应用中，通常选择采样率为信号最高频率的 **2.56** 倍或 **3** 倍，以提供足够的余量并避免混叠。

### 2.2 抗混叠滤波

#### 2.2.1 混叠的产生

当采样频率低于信号最高频率时，会出现混叠现象。混叠是指高频信号成分被错误地映射到低频区域，导致原始信号的失真。

#### 2.2.2 抗混叠滤波器的设计

为了防止混叠，在采样之前使用抗混叠滤波器来滤除信号中的高频成分。抗混叠滤波器是一个低通滤波器，其截止频率设置为信号最高频率的一半。

**代码块：**

import numpy as np
import matplotlib.pyplot as plt

# 原始信号
fs = 1000  # 采样频率
fm = 500  # 信号最高频率
t = np.linspace(0, 1, fs)
x = np.sin(2 * np.pi * fm * t)

# 采样信号
fs_low = 400  # 采样频率低于信号最高频率
x_low = x[::int(fs / fs_low)]

# 绘制原始信号和采样信号
plt.plot(t, x, label='原始信号')
plt.plot(t[::int(fs / fs_low)], x_low, label='采样信号')
plt.xlabel('时间 (s)')
plt.ylabel('幅度')
plt.legend()
plt.show()

**逻辑分析：**

此代码模拟了采样频率低于信号最高频率时混叠的产生。原始信号是一个正弦波，其最高频率为 500 Hz。采样频率设置为 400 Hz，低于信号最高频率。采样后的信号显示出混叠