MATLAB有限元分析秘籍：解决复杂工程问题，探索物理奥秘

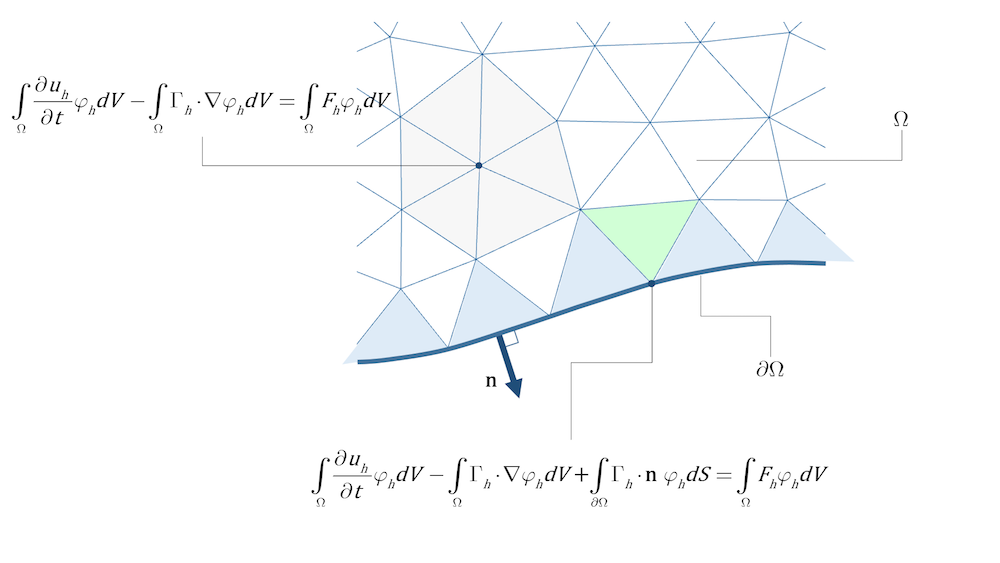
# 1. 有限元分析基础**

有限元分析 (FEA) 是一种强大的数值技术，用于解决复杂工程问题。它将连续介质离散化为有限数量的单元，称为有限元，从而创建问题的数学模型。通过求解这些单元上的方程，FEA 能够预测结构、流体和热系统在各种载荷和边界条件下的行为。

FEA 的基础在于连续介质力学，它描述了材料在力、应力和应变下的行为。通过将连续介质离散化为有限元，FEA 可以使用数值方法求解复杂的偏微分方程，从而获得连续介质行为的近似解。

# 2. MATLAB有限元分析平台

**2.1 MATLAB中的有限元工具箱**

MATLAB提供了一个强大的有限元分析工具箱，称为**Partial Differential Equation Toolbox (PDE Toolbox)**。该工具箱包含一系列函数和方法，用于求解偏微分方程（PDE），这是描述物理现象的数学方程。PDE Toolbox特别适用于有限元分析，因为它提供了以下功能：

- **网格生成：**创建用于有限元分析的几何网格。
- **有限元方程求解器：**求解有限元方程组，以获得问题的数值解。
- **后处理工具：**可视化和分析有限元分析结果。

**2.2 有限元建模的步骤**

使用MATLAB进行有限元分析通常涉及以下步骤：

1. **定义问题：**确定要解决的物理问题，并收集相关数据。
2. **创建几何模型：**使用MATLAB中的网格生成工具创建问题的几何模型。
3. **定义材料属性：**指定模型中使用的材料的力学性质。
4. **定义边界条件：**指定模型边界上的约束和载荷。
5. **求解有限元方程：**使用PDE Toolbox中的求解器求解有限元方程组。
6. **后处理结果：**使用MATLAB中的可视化和分析工具查看和分析有限元分析结果。

**代码块：**

% 定义几何模型
geometry = createpde('geometryfrommesh','mymesh.msh');

% 定义材料属性
material = createpde('material','mymaterial');
material.YoungsModulus = 200e9; % 帕斯卡
material.PoissonsRatio = 0.3;

% 定义边界条件
bc = createpde('bcfromdirichlet','mybc');
bc.u = 0; % 固定边界

% 定义载荷
load = createpde('loadfrombodyforce','myload');
load.bodyforce = [0, -1000]; % 牛顿/米^3

% 求解有限元方程
solution = solvepde(geometry,material,bc,load);

% 后处理结果
figure;
pdeplot3d(geometry,solution.u);
title('位移解');
xlabel('x');
ylabel('y');
zlabel('z');

**逻辑分析：**

这段代码演示了使用PDE Toolbox进行有限元分析的步骤。它创建了一个几何模型、定义了材料属性、指定了边界条件和载荷，然后求解有限元方程并绘制位移解。

**参数说明：**

- `createpde`：创建PDE对象。
- `geometryfrommesh`：从网格文件中创建几何模型。
- `material`：创建材料对象。
- `YoungsModulus`：杨氏模量。
- `PoissonsRatio`：泊松比。
- `bcfromdirichlet`：创建狄利克雷边界条件。
- `u`：位移约束。
- `loadfrombodyforce`：创建体积力载荷。
- `bodyforce`：体积力。
- `solvepde`：求解PDE方程组。
- `pdeplot3d`：绘制3D有限元解。

# 3. 有限元分析理论**

### 3.1 连续介质力学基础

**连续介质的概念**

连续介质是一种理想化的材料模型，假设材料由连续分布的微观粒子组成，这些粒子在宏观尺度上表现出连续性。在连续介质中，材料属性（如密度、应力、应变）在空间上是连续变化的，没有明显的间断或不连续性。

**应力与应变**

应力是作用在单位面积上的力，而应变是材料变形程度的量度。在弹性连续介质中，应力和应变之间存在线性关系，称为胡克定律：

σ = Eε

其中：

* σ 是应力
* ε 是应变
* E 是杨氏模量，表示材料的刚度

**平衡方程**

平衡方程描