【B树与B+树考点】：广工大试卷中的深度考察点


# 摘要
B树与B+树是计算机科学中用于组织和存储数据的重要数据结构，尤其在数据库索引和文件系统中发挥着关键作用。本文系统地探讨了B树和B+树的基本概念、性质、以及它们的理论基础，比较了二者在结构和操作效率上的差异，并详细分析了它们的插入与删除算法。进一步，本文深入研究了B树和B+树在实际应用中的案例，包括数据库索引和文件系统中的优化策略，并探讨了它们的变种及前沿应用趋势。本文旨在为B树与B+树的深入研究和应用提供全面的理论支持与实践指导。

# 关键字
B树；B+树；数据结构；数据库索引；文件系统；算法实现

参考资源链接：[广工数据结构期末考试真题及答案解析](https://wenku.csdn.net/doc/w7murq9pd7?spm=1055.2635.3001.10343)
# 1. B树与B+树的基本概念与性质

## 1.1 B树的定义与性质
B树（B-Tree）是一种自平衡的树数据结构，能够保持数据有序，并且允许搜索、顺序访问、插入和删除在对数时间内完成。它是为磁盘或其他直接存取辅助存储设备设计的一种平衡查找树，特别适合读写相对较大的数据块的系统。

## 1.2 B+树的定义与性质
B+树是B树的一种变体，其特点是所有的数据记录都出现在叶子节点上，并且这些叶子节点之间通过指针形成一个有序链表。B+树可以比B树拥有更多的子节点，因而其高度更低，这使得其在大量数据的查找操作中更加高效。

## 1.3 B树与B+树的比较分析
在结构上，B+树比B树有更高的分支因子和更低的高度，这在存储大量数据时具有优势。在操作效率上，B+树的插入和删除操作通常比B树更高效，因为它不需要在非叶子节点中存储数据记录。

# 2. B树与B+树的理论基础

### 2.1 B树的定义与性质

#### 2.1.1 B树的定义
B树（B-tree）是一种自平衡的树数据结构，它能够保持数据有序，允许搜索、顺序访问、插入和删除在对数时间内完成。B树由鲁道夫·贝尔发明，广泛应用于数据库和文件系统的索引结构。B树特别适合读写相对较大的数据块的存储系统，如磁盘存储等，因此是大多数关系数据库中使用的索引数据结构。

#### 2.1.2 B树的关键特性分析
B树有如下几个关键特性：
- **节点的平衡性**：所有叶子节点在同一层，并且每个节点最多有m个子节点，其中m称为B树的阶。
- **有序性**：所有键值都是有序的，且每个非叶子节点内的键可以作为分隔符来决定子树中值的范围。
- **数据分散性**：每个节点的键值将数据分割为不同范围，这些范围对应着子节点。
- **子节点数量**：每个节点除了根节点外至少有`ceil(m/2)-1`个子节点。

### 2.2 B+树的定义与性质

#### 2.2.1 B+树的定义
B+树是B树的一种变体，在数据结构上与B树非常相似，但在内部实现上有所不同。其特点是所有数据都存储在叶子节点上，并且所有叶子节点都链接在一起，形成了一个有序链表。这种设计提高了范围查询的效率，并且因为非叶子节点不存储数据，使得树的高度更低，提高了查询效率。

#### 2.2.2 B+树与B树的区别和联系
B+树与B树主要有以下区别：
- **叶子节点**：B+树的叶子节点包含了全部数据项和指向下一个叶子节点的指针，而B树的叶子节点可能包含数据，也可能不包含。
- **数据存储**：B+树的数据只存储在叶子节点，非叶子节点仅存储键值和指向子节点的指针；B树的数据可以存储在任何节点。
- **效率**：B+树的查询效率通常高于B树，尤其是在进行范围查找时，因为所有数据都在叶子节点，可以顺序读取，无需回溯。

联系在于：
- **结构相似**：都保持树的平衡性，都有n-1个键值和n个指针，其中n是树的阶。
- **有序性**：都保证键值有序，便于快速查找、插入和删除。

### 2.3 B树与B+树的比较分析

#### 2.3.1 结构上的对比
B树与B+树在结构上的对比主要体现在节点内部的组织方式和数据存储位置：
- **节点内部结构**：B树的每个节点都存储键值和数据，而B+树只有叶子节点存储数据，非叶子节点仅存储键值和指针。
- **数据存储**：B+树的数据仅在叶子节点，因此叶子节点相互链接形成链表，有利于顺序访问；B树的数据可能分布在树的任何节点。

#### 2.3.2 操作效率的对比
操作效率的对比主要体现在不同的操作类型上：
- **单点查找**：由于B树的键值分布于所有节点，所以在单个值的查找上B树可能略优于B+树。
- **范围查询**：B+树的叶子节点形成链表，这使得顺序读取非常高效，适合做范围查询。
- **插入和删除**：B+树在插入和删除时往往更高效，因为其非叶子节点的键值只作为分隔符使用，节点中可以存储更多子节点，减少了树的高度。

B树和B+树各有优劣，选择哪一种取决于特定应用场景的需求，如是否需要频繁的范围查询等。

以上为第二章内容，它为读者提供了对B树和B+树基本定义和性质的深入理解，并且涵盖了它们的区别和联系，为后文更高级的内容和应用案例分析打下了坚实的基础。接下来的章节将讨论B树和B+树的算法实现、操作效率优化以及它们在实际中的应用。

# 3. B树与B+树的算法实现

## 3.1 B树的插入与删除算法

### 3.1.1 B树的插入操作详解

在本小节中，我们将深入分析B树的插入操作。B树的插入操作需遵循几个关键步骤以维持树的平衡性。

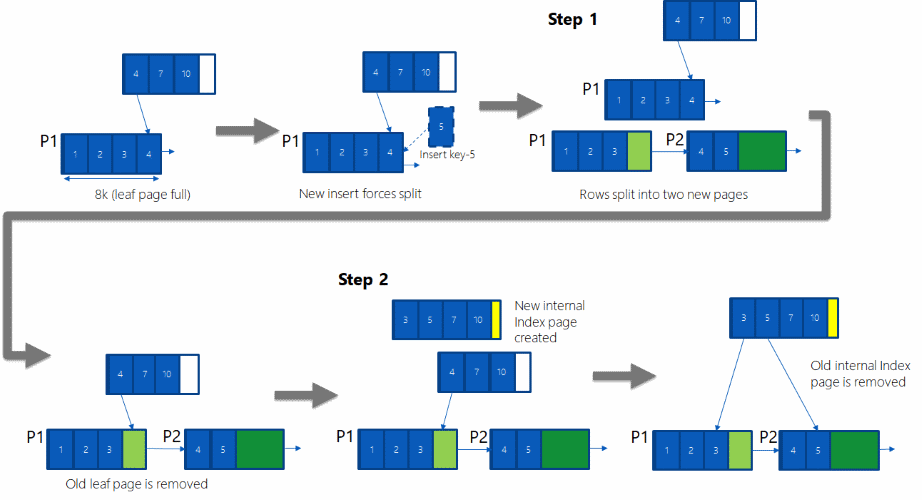
首先，我们从根节点开始，查找应该插入的叶子节点。由于B树的每个节点包含指向子节点的指针，我们沿着这些指针移动，直至到达一个叶子节点。接着，在该叶子节点上，我们将新的键值对插入到适当的位置，确保键值对之间仍然按顺序排列。

如果叶子节点的键数未满，该操作即告完成。然而，若叶子节点的键数达到最大容量（即树阶数t-1），我们需要将其分裂成两个节点，并将中间的键提升至父节点。这一过程可能需要递归地在父节点上执行，从而可能引发一连串的节点分裂。

为确保代码的可读性，下面展示了一个简化的B树插入操作的Python示例代码：

class BTreeNode:
    def __init__(self, leaf=False):
        self.leaf = leaf
        self.keys = []
        self.child = []

def insert(root, k):
    if len(root.keys) == (2 * t - 1):  # 检查节点是否已满
        temp = BTreeNode()
        root.child.insert(0, temp)
        temp.child.insert(0, root)
        split_child(temp, 0)
        i = 0
        if k > temp.keys[0]:
            i += 1
        insert(temp.child[i], k)
    else:
        insert_non_full(root, k)

def split_child(x, i):
    t = (len(x.keys) + 1) // 2
    y = x.child[i]
    z = BTreeNode(y.leaf)
    z.key