【拓扑排序与关键路径】：广东工业大学试卷中的问题解析


# 摘要
本文全面探讨了拓扑排序与关键路径的基本概念、算法解析以及实际应用，旨在为工程管理、软件开发和网络工程等领域的相关问题提供解决方案。首先介绍了拓扑排序与关键路径在理论上的定义和作用，并对其算法实现进行了详细解析，包括Kahn算法和DFS算法在拓扑排序中的应用，以及事件驱动法和节点标记法在关键路径计算中的应用。接着，通过案例分析，本文深入解析了典型问题的解决思路和技巧，并展示了代码实现的过程。最后，本文探讨了拓扑排序与关键路径在软件工程、网络工程以及教育和生产调度等其他领域的潜在应用，强调了这些技术工具在优化管理流程和提升效率方面的重要性。

# 关键字
拓扑排序；关键路径；有向无环图；算法实现；项目管理；软件工程

参考资源链接：[广工数据结构期末考试真题及答案解析](https://wenku.csdn.net/doc/w7murq9pd7?spm=1055.2635.3001.10343)
# 1. 拓扑排序与关键路径的基本概念

## 1.1 项目管理和依赖关系
在项目管理和工作流程中，理解任务的先后顺序与依赖关系至关重要。例如，在软件开发过程中，某些模块的构建必须在其他模块之前完成。这种依赖关系可以用有向图来表示，其中节点表示项目中的活动，而有向边则表示活动间的依赖关系。为了有效地管理和调度这些活动，我们引入了拓扑排序和关键路径的概念。

## 1.2 拓扑排序与关键路径的定义
拓扑排序是针对有向无环图（DAG）的一种排序方式，其结果是一系列的节点，这些节点按照它们之间的依赖关系排列，使得对于任意一条有向边(u, v)，节点u都出现在节点v之前。关键路径则是项目中从开始到结束的最长路径，它决定了项目的最短完成时间。

## 1.3 关键路径的意义
关键路径法（CPM）是一种重要的项目管理工具，它通过识别项目中的关键活动来帮助项目经理监控项目的进度。关键路径上的活动不能延迟，因为它们决定了整个项目的完成时间。通过这种分析，项目经理能够确定哪些任务是项目进度的瓶颈，并据此做出相应的调整或资源分配。

# 2. 拓扑排序的算法解析

## 2.1 拓扑排序的理论基础
拓扑排序是针对有向无环图（DAG）的一种排序方式，它将图中的顶点排成一个线性序列，使得对于任何一条有向边(u, v)，顶点u都在顶点v之前。拓扑排序的目的是为了揭示图中各顶点之间的依赖关系，或者说是先后顺序。

### 2.1.1 有向无环图（DAG）的定义
DAG是一种图论中的概念，指的是在图中的边都是有方向的，并且不存在任何从一个顶点出发经过若干条边又回到该顶点的环路。DAG在项目管理、软件构建系统、编译器的设计等领域有着广泛的应用。

### 2.1.2 拓扑排序的定义和作用
拓扑排序是一种将DAG中顶点排成线性序列的方法，这一序列保证对于每一条有向边(u, v)，顶点u都在顶点v之前。拓扑排序主要作用是识别和处理依赖关系，特别是在那些需要根据依赖关系顺序执行任务的场景中，如作业调度、项目管理等。

## 2.2 拓扑排序的实现方法
拓扑排序可以通过多种算法实现，但这里主要讨论两种经典算法：Kahn算法和深度优先搜索（DFS）算法。

### 2.2.1 Kahn算法
Kahn算法适用于找到一个有向无环图的所有顶点的拓扑排序。算法步骤如下：
1. 找出所有入度为0的顶点，并将其放入队列Q。
2. 当队列Q非空时，执行以下步骤：
- 从Q中删除一个顶点，输出它。
- 对于该顶点的每一个邻接点：
- 减少邻接点的入度。
- 如果邻接点的入度为0，则将其放入Q中。
3. 如果所有顶点都被输出，则完成拓扑排序；否则，图中存在环，无法进行拓扑排序。

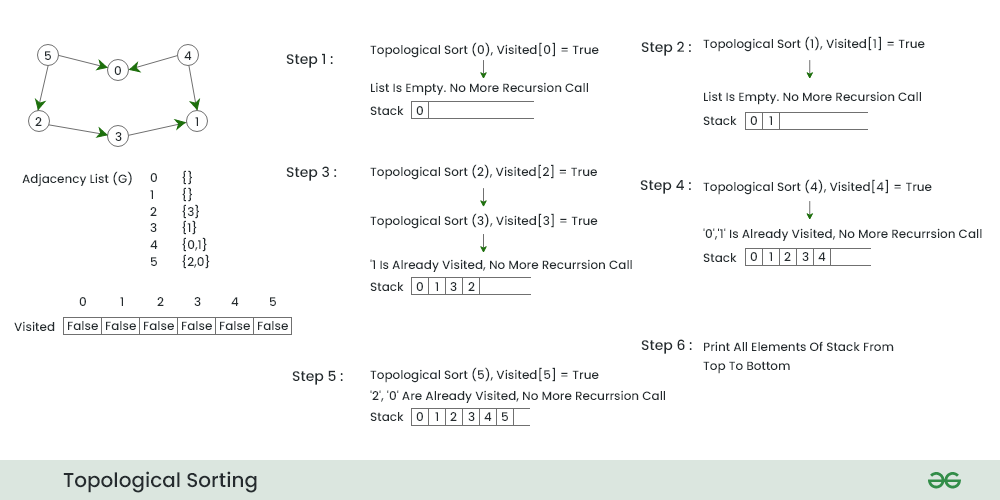
### 2.2.2 DFS算法
DFS算法通过递归的方式进行拓扑排序，其基本步骤如下：
1. 从一个未访问的顶点开始，对该顶点执行深度优先搜索。
2. 在搜索过程中，记录访问的顺序。
3. 完成对一个顶点的所有邻接点的搜索后，将该顶点标记为已访问。
4. 按照访问顺序的逆序输出顶点，即可得到拓扑排序的结果。

## 2.3 拓扑排序的代码实践
本章节将通过一个实际的代码实践来加深对拓扑排序算法的理解。

### 2.3.1 算法伪代码分析
对于Kahn算法的伪代码如下：

function topologicalSortKahn(vertices, edges):
    inDegree = {v: 0 for v in vertices}
    graph = defaultdict(set)
    for u, v in edges:
        graph[u].add(v)
        inDegree[v] += 1

    queue = [v for v in vertices if inDegree[v] == 0]
    order = []

    while queue:
        u = queue.pop(0)
        order.append(u)
        for v in graph[u]:
            inDegree[v] -= 1
            if inDegree[v] == 0:
                queue.append(v)

    if len(order) == len(vertices):
        return order
    else:
        return None  // Graph has a cycle and cannot be topologically sorted

### 2.3.2 实际代码实现与注释
以下是Kahn算法的一个Python代码实现，包含了详细的注释：

from collections import defaultdict, deque

def topological_sort_kahn(vertices, edges):
    # 初始化每个顶点的入度为0
    in_degree = {v: 0 for v in vertices}
    # 构建图的邻接表和入度表
    graph = defaultdict(list)
    for u, v in edges:
        graph[u].append(v)
        in_degree[v] += 1
    # 将所有入度为0的顶点加入队列
    queue = deque([v for v in vertices if in_degree[v] == 0])
    # 存储排序结果
    sorted_order = []
    # 开始进行拓扑排序
    while queue:
        u = queue.popleft()  # 取出队列中顶点
        sorted_order.append(u)
        # 遍历当前顶点的所有邻接点，减小它们的入度
        for v in graph[u]:
            in_degree[v] -= 1
            if in_degree[v] == 0:  # 如果入度变为0，加入队列
                queue.append(v)
    # 如果排序后的顶点数与总顶点数不一致，说明图中存在环
    if len(sorted_order) != len(vertices):
        return None  # Graph has a cycle and cannot be topologically sorted
    else: