【散列表实战运用】：广工大试卷中的解题技巧与应用


# 摘要
散列表是计算机科学中一种高效的数据结构，通过特定的散列函数将数据映射到数组中的位置，实现快速的查找、插入和删除操作。本文系统性地介绍了散列表的基本概念、核心算法以及实现原理，并探讨了散列函数的设计、冲突解决机制和性能分析。此外，文中还详细分析了散列表在解决数据去重、查找和编码问题中的应用，以及在排序算法、数据流处理和图算法中的实战问题解析。文章最后讨论了散列表的高级应用、优化策略，并通过项目案例分析了散列表的实际应用价值。整体而言，本文旨在为读者提供散列表深入理解以及在不同领域应用的全面指南。

# 关键字
散列表；散列函数；冲突解决；性能分析；数据去重；算法优化

参考资源链接：[广工数据结构期末考试真题及答案解析](https://wenku.csdn.net/doc/w7murq9pd7?spm=1055.2635.3001.10343)
# 1. 散列表的基本概念和原理

在探讨散列表之前，我们先从基础开始，了解什么是散列表及其工作的基本原理。散列表，又称哈希表，是一种基于键值对的数据结构。它利用一种哈希函数将输入的键（Key）转换为数组的索引位置，从而实现快速的插入、删除和查找操作。

## 散列表的基本组成
散列表通常由两部分组成：**数组**和**哈希函数**。数组负责存储数据，哈希函数则负责计算数据的位置。哈希函数的设计十分关键，因为它直接关系到散列表的性能。好的哈希函数能够均匀分布数据，减少冲突，从而提高访问速度。

## 散列表的工作原理
在散列表中，数据以键值对的形式存储。当我们插入一个键值对时，哈希函数会将键转换成一个数组索引，然后将键值对存入该索引位置。查找和删除操作也依赖于哈希函数来快速定位到数据所在位置。

在后续的章节中，我们将深入了解散列函数的设计、处理冲突的策略以及如何对散列表进行性能分析。

# 2. 散列表的核心算法和实现

## 2.1 散列函数的设计

### 2.1.1 理解散列函数的作用

散列函数是散列表中最为关键的组件之一，它将键映射到存储位置。理想情况下，一个良好的散列函数能够将输入键均匀分布到散列表的所有位置，从而最大限度地减少冲突。散列函数的基本任务是提供一个快速的转换过程，将大数据对象转换为表中较小的索引值。

### 2.1.2 探索不同散列函数的特点

不同的散列函数有其独特的特点和使用场景。例如，模运算散列函数简单且高效，但是容易受到输入数据分布不均的影响；平方散列函数能够更好地分散数据，但计算成本较高；除留余数法则是结合了模运算和一个大质数的乘法操作，提高了分散性。

### 2.1.3 实践中的散列函数选择

在实践中，散列函数的选择往往取决于数据的特性以及应用的具体需求。例如，对于小型的静态数据集，使用简单的模运算散列函数可能就足够了；而在大型动态数据集中，可能需要设计更加复杂的散列函数，如结合多个散列函数的组合散列函数，以避免潜在的集群问题。

// 示例代码：简单的模运算散列函数实现
unsigned int simpleHash(unsigned int key, unsigned int tableSize) {
    return key % tableSize; // 使用模运算得到索引位置
}

## 2.2 冲突解决机制

### 2.2.1 冲突的产生与分类

在散列表中，当两个不同的键通过散列函数计算得到同一个索引位置时，冲突就产生了。冲突可以分为两大类：同义词冲突和聚合冲突。同义词冲突是指由于散列函数的映射特性导致的不同输入产生相同的输出；而聚合冲突则是由于散列表的大小有限，无法存储所有可能的键值对。

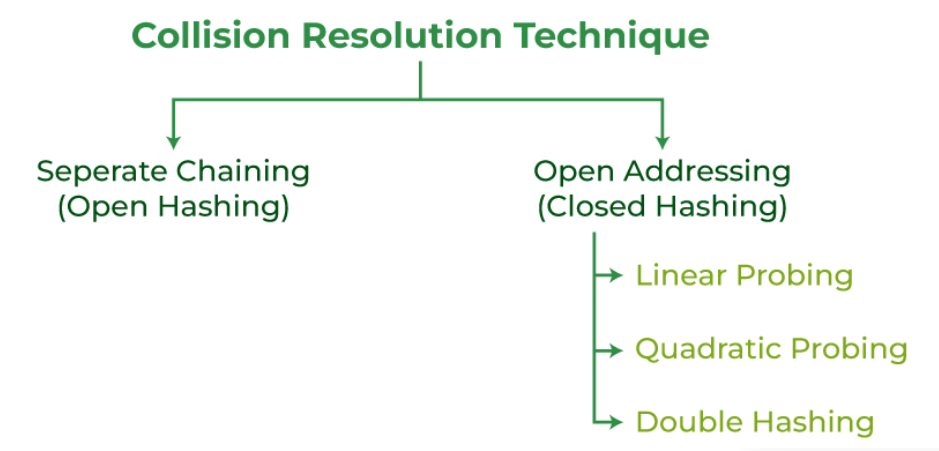
### 2.2.2 开放定址法和链表法的应用

解决冲突的常用方法有开放定址法和链表法。开放定址法是寻找下一个空的散列表位置来存储冲突数据的方法。链表法则是在每个散列表位置上维护一个链表，将冲突的元素加入到该链表中。每种方法都有其优势和局限性。开放定址法适合于散列表负载因子不是很大的情况，而链表法则适用于所有负载因子的情况。

### 2.2.3 实际案例分析

例如，Redis数据库中的散列表就是使用链表法来处理冲突的。当键通过散列函数计算出的索引位置已经被占用时，新的键值对就会被追加到该位置的链表中。链表法特别适合于内存中数据的处理，因为链表节点的插入和删除操作都比较高效。

## 2.3 散列表的性能分析

### 2.3.1 时间复杂度和空间复杂度

散列表的操作主要有插入、删除和查找，其性能分析主要涉及时间复杂度和空间复杂度。在理想情况下，即没有冲突发生时，散列表的性能是最佳的，所有操作都可以在常数时间复杂度O(1)内完成。但是，随着散列表中元素数量的增加，时间复杂度会逐渐接近于线性时间复杂度O(n)，这通常发生在负载因子过高时。

### 2.3.2 实际应用中的性能优化

为了优化散列表的性能，可以采取动态扩展和收缩的策略。当散列表中的元素数量超过某个阈值时，散列表会扩展其大小，并重新分布元素以减少冲突；相应地，当元素数量减少到某个阈值以下时，散列表会收缩以节省空间。此外，对于内存紧张的应用场景，采用一致性散列可以减少因动态扩展和收缩带来的性能开销。

// 示例代码：动态调整散列表大小
void resizeHashTable(HashTable *table, unsigned int newSize) {
    // 新建一个更大的散列表
    HashTable newTable = createHashTable(newSize);
    // 将旧表中的数据重新散列到新表
    for (int i = 0; i < table->size; i++) {
        Entry *entry = table->entries[i];
        while (entry != NULL) {
            Entry *next = entry->next;
            unsigned int index = hashFunction(entry->key, newSize);
            entry->next = newTable->entries[index];
            newTable->entries[index] = entry;
            entry = next;
        }
    }
    // 删除旧表，并将新表赋值给原指针
    freeHashTable(table);
    *table = newTable;
}

在本章中，我们详细探讨了散列表的核心算法和实现，重点包括散列函数的设计、冲突解决机制以及性能分析。通过对散列函数深入的理解和分析，我们了解到选择合适的散列函数对于减少冲突和提高散列表性能的重要性。冲突解决机制作为散列表的核心难题之一，我们学习了开放定址法和链表法的不同应用场景和优缺点，并通过实际案例加深了理解。性能分析部分则让我们认识到，尽管散列表在理想状态下具有极高的效率，但在实际应用中，仍需通过动态扩展和收缩等优化策略来维持其性能。接下来的章节，我们将深入了解散列表在解决实际问题中的应用，以及散列表的高级应用和优化策略。

# 3. 散列表在解题中的应用

## 3.1 散列表解决数据去重问题

### 3.1.1 去重问题的场景和需求分析

在处理大量数据时，数据去重是一个常见的需求。无论是处理日志文件、数据库记录还是网络爬虫收集的数据，都可能遇到重复数据。去重问题的场景和需求分析是理解和实施去重策略的关键。场景上，去重可能出现在数据导入、实时数据流处理、数据清洗等环节。在需求上，去重要确保数据的唯一性，同时要兼顾处理效率和存储成本。

### 3.1.2 散列表去重的具体实现

实现数据去重的一个高效方法是使用散列表。具体实现步骤如下：

1. 初始化一个空的散列表，用于存储已遍历的元素。
2. 遍历待去重的数据集。
3. 对于每个元素，计算其散列值，并在散列表中查找。
4. 如果散列表中不存在该散列值对应的键，将元素加入散列表；如果存在，说明元素重复，可以丢弃或进行相应处理。

def remove_duplicates(data_list):
    hash_table = {}  # 创建空散列表
    unique_data = []  # 用于存储去重后的数据

    for item in data_list:
        hash_value = hash(item)  # 计算元素的散列值
        if hash_value not in hash_table:
            hash_table[hash_value] = True  # 加入散列表
            unique_data.append(item)  # 加入去重后的数据列表

    return unique_data

# 示例使用
data = [1, 2, 3, 2, 1, 4]
print(remove_duplicates(data))  # 输出去重后的数据

在上述代码中，我们使用Python内置的`hash()`函数作为散列函数，并利用字典的键的唯一性来实现数据去重。当散列值在字典中不存在时，说明元素尚未出现过，因此将其加入到结果列表和字典中。

## 3.2 散列表在查找问题中的应用

### 3.2.1 查找问题的类型及挑战

查找问题是计算机科学中另一个基础且重要的问题类型。常见的查找问题包括精确查找和范围查找。查找问题的挑战在于如何快速定位目标元素，并且在大数据集上保持高效的查找性能。在动态变化的数据集合中，查找问题变得更具挑战性。

### 3.2.2 散列表查找算法的实现步骤

散列表可以提供一种时间复杂度接近O(1)的查找方法，这对于快速查找是极其有用的。散列表查找算法的实现步骤如下：

1. 根据要查找的键计算散列值。
2. 使用计算出的散列值定位到散列表中对应的桶。
3. 在桶内进行线性或二分查找，如果元素存在，返回元素；如果不存在，返回查找失败的信息。

def hash_search(hash_table, key):
    hash_value = hash(key)  # 计算散列值
    bucket = hash_table.get(hash_value, [])  # 获取对应的桶
    for item in bucket:
        if item == key:  # 线性查找
            return True  # 查找成功

    return False  # 查找失败

# 示例使用
hash_table = {hash("apple"): ["apple"], hash("banana"): ["banana"], hash("cherry"): ["cherry"]}
print(hash_search(hash_table, "banana"))  # 输出：True
print(hash_search(hash_table, "orange"))  # 输出：False

## 3.3 散列表在编码问题中的应用

### 3.